revisional-3o-bimestre-marcelo-1

Revisional – 3° Bim - MARCELO
6º Ano
1) Represente no papel quatro pontos distintos e, por eles, determine dois segmentos de reta distintos.
2) Observe os segmentos de reta na figura. Escreva quantos são os segmentos, seus lados, vértice e
ângulo entre eles, se houver.
3) Construa:
a) Uma linha poligonal aberta simples com três segmentos consecutivos;
b) Uma linha poligonal fechada não-simples com cinco segmentos consecutivos;
c) Uma linha poligonal fechada simples com quatro segmentos consecutivos.
4) Escreva, com suas palavras, o que são segmentos colineares.
5) Ligue todos os pontos da figura de modo a conseguir uma linha poligonal fechada.
6) Determine o comprimento da linha poligonal abaixo. É uma linha poligonal aberta ou fechada?
7) Para cada polígono abaixo escreva CV para os convexos, CC para os côncavos e NP para os não
polígonos.
8) Em cada caso escreva o nome do polígono:
a) 6 lados _________________________;
b) 11 lados ________________________;
c) 18 lados ________________________
d) 20 lados ________________________?
9) Utilizando régua e compasso construa um triângulo de lados 2cm, 6cm e 7cm.
10) Utilize régua e compasso verifique se é possível construir um triângulo de lados 5cm, 2cm e 7cm.
11) Classifique cada triângulo quanto aos lados.
12) Classifique cada triângulo abaixo quanto a seus ângulos.
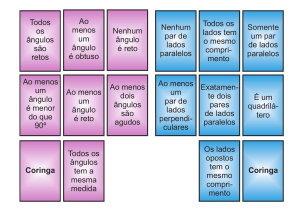
13) No balão azul coloque os nomes que são de classificações de trapézios e no balão verde os nomes que
são classificações de paralelogramos.
RETÂNGULO – ISÓSCELES – TRAPÉZIO RETÂNGULO – QUADRADO – ESCALENO - LOSANGO
14) A Bandeira nacional brasileira, também chamada de bandeira Auriverde foi adotada em 19 de
novembro de 1889 tendo 21 estrelas e em 1992 foi adotada a versão com 27 estrelas representando
os estados brasileiros. Observe a imagem de nossa bandeira e diga quantos, e quais, polígonos
podemos encontrar.
15) Assinale V para cada alternativa verdadeira e F para as falsas.
a) Todo quadrado é um losango;
b) Todo paralelogramo tem 4 diagonais;
c) Todo retângulo é um quadrado;
d) Um triângulo é um polígono com 1 diagonal;
e) Triângulo acutângulo é aquele que tem todos os ângulos agudos;
f) O trapézio retângulo é aquele que tem um par de ângulos retos.
Revisional – 3° Bim - MARCELO
7º Ano
1) Marque V (verdadeira) ou F (falsa) para cada afirmação.
a) O complemento de um ângulo x é escrito como (90°–x);
b) A soma de dois ângulos suplementares é 360°;
c) A soma de dois ângulos replementares é 360°;
d) Se um polígono tem um ângulo interno medindo 70°, então o ângulo externo correspondente
mede exatamente 110°.
2) Determine o complemento, o suplemento e o replemento de cada ângulo.
a) 29°
b) 89°10’
c) 54°54’54”
d) 1°
3) Se o triplo do suplemento de um ângulo mede 78°, qual o valor desse mesmo ângulo?
4) O suplemento de um ângulo é o dobro do complemento do mesmo ângulo, determine o ângulo em
questão. Qual o nome especial dado para este ângulo?
5) Qual a medida do ângulo externo de um triângulo equilátero?
6) Determine os valores dos ângulos destacados (coloridos).
7) Todo par de ângulos adjacentes são consecutivos. Explique.
8) Utilize os pontos da figura para desenhar segmentos de reta de modo a obter ao menos dois pares de
ângulos consecutivos.
9) Determine, a partir da figura abaixo, três pares de ângulos adjacentes.
10) Ao interior de quais ângulos pertence o ponto H?
11) Sabendo que os ângulos destacados são adjacentes, determine o valor de x.
12) A figura representa parte do mapa do bairro Santa Equipe. Identifique nele ruas que representem:
a) Retas concorrentes;
b) Retas paralelas;
c) Retas concorrentes e perpendiculares.
13) Determine o único par de retas perpendiculares na figura abaixo.
14) Quantos pontos em comum têm:
a) Duas retas concorrentes perpendiculares?
b) Duas retas paralelas coincidentes?
c) Duas retas concorrentes?
d) Duas retas paralelas distintas?
Revisional – 3° Bim - MARCELO
8º Ano
1) Dê nome aos elementos do quadrilátero abaixo (vértices, lados, diagonais, ângulos internos, ângulos
externos).
2) Determine o perímetro do quadrilátero ABCD.
3) O que você entende por polígono côncavo?
4) Marque apenas os quadriláteros convexos.
5) Um aluno do 8° ano fez a seguinte afirmação: “Todo quadrilátero convexo com dois pares de lados
paralelos é um trapézio”. A afirmação está correta? Em caso negativo, corrija-a.
6) Sabendo que os ângulos internos de um quadrilátero são 2x, 3x+10°, 30°-x e 40°, determine o valor de
cada ângulo.
7) Um quadrilátero tem perímetro 102cm e as medidas de seus lados são números naturais consecutivos.
Quais são os valores dos lados?
8) Calcule as medidas de x e y na figura.
9) Um trapézio isósceles tem 124 cm de perímetro, e a base média mede 25 cm. Calcule as medidas dos
lados oblíquos desse trapézio.
10) Uma diagonal de um paralelogramo forma 26° com um lado e 42° com o outro. Calcule as medidas dos
ângulos desse paralelogramo.
11) Se a medida de um dos ângulos de um trapézio retângulo é 22°, quais são as medidas dos outros três
ângulos?
12) Um losango tem um de seus ângulos medindo 54°, quais as medidas dos outros três ângulos?
13) O tangram é um quebra-cabeças com 7 peças geométricas. Com ele é possível formar mais de 1700
figuras diferentes como animais, objetos, pessoas e símbolos. Observe a figura e responda.
a)
b)
c)
d)
e)
Quantas peças do tangram são quadriláteros?
Utilizando exatamente três peças podemos formar um trapézio retângulo? Se sim, quais?
Determine a medida do ângulo x.
Como chamamos o segmento
em relação ao quadrilátero ABCD?
Na figura estão formados dois losangos de tamanhos diferentes, identifique-os.
14) Assinale V ou F.
a)
b)
c)
d)
e)
f)
Todo quadrado é um losango;
Todo retângulo é um trapézio;
O trapézio tem dois pares de lados paralelos;
O retângulo tem 4 ângulos retos;
Todo paralelogramo é um retângulo;
As diagonais de um retângulo se cortam ao meio.
15) Qual propriedade do losango garante encontrarmos o ângulo x sem fazermos medições ou cálculos?
16) Classifique a posição de cada ponto quanto à circunferência. Depois relacione a distância de cada
ponto ao centro O (utilize os símbolos =, >, <).
17) Utilizando o exercício anterior, determine:
a) Uma corda de circunferência;
b) A medida do raio;
c) A medida do diâmetro.
18) Resolver as questões 04, 07, 09, 13, 14, 16 e 20 da sessão extra do material de aula (páginas 92 a 94).