Aproximações Lineares e Diferenciais

1. Aproximações Lineares
UNIVERSIDADE DO ESTADO DE MATO GROSSO
CAMPUS UNIVERSITÁRIO DE SINOP
FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS
CURSO DE ENGENHARIA CIVIL
DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I
10
9
8
7
6
5
Aproximações Lineares e Diferenciais
4
3
2
1
(1,1)
0
-4
-3
-2
-1
0
1
2
3
4
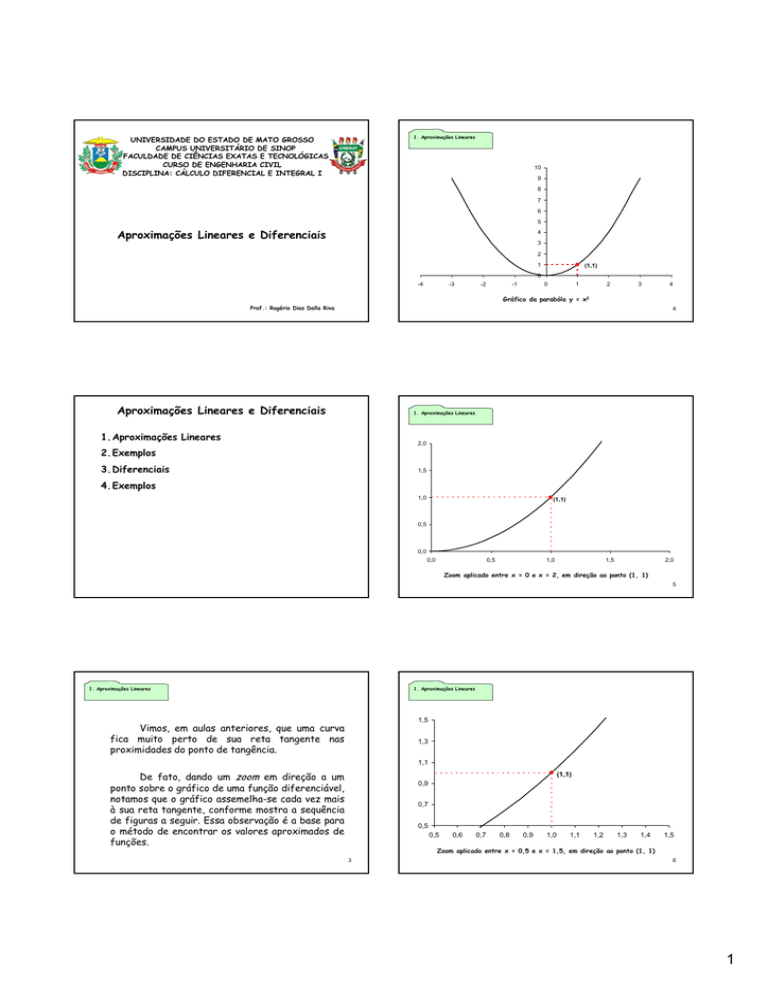
Gráfico da parabóla y = x2
Prof.: Rogério Dias Dalla Riva
4
Aproximações Lineares e Diferenciais
1. Aproximações Lineares
1.Aproximações Lineares
2,0
2.Exemplos
3.Diferenciais
1,5
4.Exemplos
1,0
(1,1)
0,5
0,0
0,0
0,5
1,0
1,5
2,0
Zoom aplicado entre x = 0 e x = 2, em direção ao ponto (1, 1)
5
1. Aproximações Lineares
1. Aproximações Lineares
1,5
Vimos, em aulas anteriores, que uma curva
fica muito perto de sua reta tangente nas
proximidades do ponto de tangência.
1,3
1,1
(1,1)
De fato, dando um zoom em direção a um
ponto sobre o gráfico de uma função diferenciável,
notamos que o gráfico assemelha-se cada vez mais
à sua reta tangente, conforme mostra a sequência
de figuras a seguir. Essa observação é a base para
o método de encontrar os valores aproximados de
funções.
0,9
0,7
0,5
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
Zoom aplicado entre x = 0,5 e x = 1,5, em direção ao ponto (1, 1)
3
6
1
1. Aproximações Lineares
1. Aproximações Lineares
1,10
Em outras palavras, usamos a reta tangente
em (a, f(a)) como uma aproximação para a curva
y = f(x) quando x está próximo de a. Uma equação
dessa reta tangente é:
1,05
1,00
(1,1)
y = f (a ) + f ′(a )( x − a )
0,95
Equação 1
0,90
0,90
0,95
1,00
1,05
1,10
Zoom aplicado entre x = 0,9 e x = 1,1, em direção ao ponto (1, 1)
7
1. Aproximações Lineares
10
1. Aproximações Lineares
A idéia é que pode ser fácil calcular um valor
de f(a) de uma função, mas é difícil (ou mesmo
impossível) computar os valores próximos de f.
e a aproximação
f ( x ) ≅ f (a ) + f ′(a )( x − a )
é denominada aproximação linear ou aproximação
pela reta tangente de f em a. A função linear cujo
gráfico é essa reta tangente, isto é,
Assim decidimos pelos valores facilmente
computados da função L, cujo gráfico é a reta
tangente de f em (a, f(a)), conforme mostrado na
figura a seguir.
L( x ) = f (a) + f ′(a )( x − a )
Equação 2
8
1. Aproximações Lineares
é chamada de linearização de f em a.
11
2. Exemplos
Exemplo 1: Suponha que após ter recheado um
peru a sua temperatura é de 50 oF e você então o
coloca no forno a 325 oF. Depois de uma hora o
termômetro do peru indica que sua temperatura
está a 93 oF e, após 2 horas, a 129 oF. Prediga a
temperatura do peru após 3 horas.
Reta tangente y = L(x) à curva y = f(x) em (a, f(a))
9
12
2
2. Exemplos
2. Exemplos
Solução: Se T(t) representa a temperatura do
peru após t horas, nos foi dado que T(0) = 50,
T(1) = 93 e T(2) = 129. Para fazer uma aproximação
linear com a = 2, precisamos de uma estimativa
para a derivada T ’(2).
Obtemos uma estimativa mais precisa para
T ’(2) desenhando os dados, como na figura a
seguir, e estimando a inclinação da reta tangente
em t = 2 como
T ′(2) ≅ 33
Então nossa aproximação linear torna-se
T (3) ≅ T (2) + T ′(2) ⋅ 1 ≅ 129 + 33 = 162
13
2. Exemplos
e nossa estimativa melhorada para a temperatura é
de 162 oF.
16
2. Exemplos
Uma vez que
T ′(2) = lim
t →2
T (t ) − T (2)
t −2
podemos estimar T ’(2) pelo quociente de diferenças com t = 1:
T ′(2) ≅ lim
t →2
T (1) − T (2) 93 − 129
=
= 36
1− 2
−1
14
2. Exemplos
Estimativa para T ’(2)
17
2. Exemplos
Isso equivale a aproximar a taxa instantânea
de variação da temperatura pela taxa média de
variação entre t = 1 e t = 2, que é de 36 oF/h. Com
essa estimativa, a aproximação linear para a
temperatura após 3 horas é:
Uma vez que a curva da temperatura fica
abaixo da reta tangente, parece que a temperatura
real após 3 horas será um pouco menor do que a
162 oF, talvez mais próxima a 160 oF.
T (3) ≅ T (2) + T ′(2)(3 − 2)
T (3) ≅ 129 + 36 ⋅ 1 = 165
Logo, a temperatura esperada após 3 horas
é de 165 oF.
15
18
3
2. Exemplos
2. Exemplos
A aproximação linear está ilustrada na
figura a seguir. Vemos que, realmente, a
aproximação pela reta tangente é uma boa
aproximação para a função dada quando x está
próximo de 1. Vemos também que nossas
aproximações são super-estimadas, pois a reta
tangente está acima da curva.
Exemplo 2: Encontre a linearização da função
f (x) = x + 3
em a = 1 e use-a para aproximar os números
3,98 e
Essas aproximações
subestimadas?
4,05.
estão
superestimadas ou
Naturalmente, uma calculadora nos daria
aproximações para 3,98 e 4,05, mas a aproximação
linear funciona em todo o intervalo.
19
2. Exemplos
22
2. Exemplos
Solução: A derivada de f ( x ) = x + 3 é
f ′( x ) =
1
1
−
1
( x + 3) 2 =
2
2 x +3
e assim temos f(1) = 2 e f ’(1) = ¼. Colocando esses
valores na Equação 2, vemos que a linearização é
L( x ) = f (1) + f ′(1)( x − 1) = 2 +
1
7 x
( x − 1) = +
4
4 4
Linearização da função pela reta tangente nas proximidades de x = 1
20
2. Exemplos
23
2. Exemplos
A aproximação linear correspondente é
x +3 ≅
Na tabela a seguir comparamos as
estimativas de uma aproximação linear no Exemplo
2 com os valores verdadeiros. Observe na tabela, e
também na figura anterior, que a aproximação pela
reta tangente dá boas estimativas quando x está
próximo de 1, mas a precisão da aproximação
deteriora à medida que x se afasta de 1.
7 x
+ (quando x está próximo de 1)
4 4
Em particular, temos
7 0,98
+
= 1,995
4
4
e
7 1,05
4,05 ≅ +
= 2,0125
4
4
3,98 ≅
21
24
4
2. Exemplos
2. Exemplos
x
De L(x)
Valor real
3,9
0,9
1,975
1,97484176…
3,98
0,98
1,995
1,99499373…
4
1
2
2,00000000…
4,05
1,05
2,0125
2,01246117…
4,1
1,1
2,025
2,02484567…
5
2
2,25
2,23606797…
6
3
2,5
2,44948974…
Solução: Uma precisão dentro de 0,5 significa que
as funções devem diferir, uma da outra, por menos
que 0,5:
7 x
x + 3 −  +  < 0,5
4 4
Assim, podemos escrever
7 x
−0,5 < x + 3 −  +  < 0,5
4 4
x + 3 − 0,5 <
ou
25
2. Exemplos
7 x
+ < x + 3 + 0,5
4 4
28
2. Exemplos
Quão boa é a aproximação obtida no
Exemplo 2? O exemplo a seguir mostra que usando
uma calculadora gráfica ou computador podemos
determinar o intervalo dentro do qual uma
aproximação linear fornece uma precisão
especificada.
o que estabelece que a aproximação linear deve
ficar entre as curvas obtidas deslocando-se a
curva y = x + 3 para cima e para baixo por uma
distância de 0,5.
A figura a seguir mostra que a reta
tangente
7 x
y= +
4 4
intercepta a curva superior y = x + 3 + 0,5 em P e
29
Q.
26
2. Exemplos
2. Exemplos
5
Exemplo 3: Para que valores de x a aproximação
linear
x +3 ≅
Q
4
y = x + 3 + 0,5
7 x
+
4 4
3
y = x + 3 − 0,5
2
é precisa dentro de 0,5? O que se pode dizer
sobre uma precisão dentro de 0,1?
P
L(x)
1
0
-4
-2
0
2
4
6
8
10
-1
Precisão da função dentro de 0,5
27
30
5
2. Exemplos
2. Exemplos
Dando um zoom e usando o cursor,
estimamos que a coordenada x de P é cerca de
-2,66 e que a coordenada x de Q é cerca de 8,66.
Assim, vemos do gráfico que a aproximação
x +3 ≅
Analogamente, da figura a seguir vemos que
a aproximação é precisa dentro de 0,1 quando
-1,1 < x < 3,9.
7 x
+
4 4
é precisa dentro de 0,5 quando -2,6 < x < 8,6.
31
2. Exemplos
34
2. Exemplos
3
2
Q
y = x + 3 + 0,1
P
1
y = x + 3 − 0,1
2
P
L(x)
0
-2,80
-2,70
-2,60
-2,50
-2,40
-2,30
-2,20
-2,10
-2,00
1
-2
-1
0
1
2
3
4
5
-1
Estimativa da coordenada x de P pela aplicação de zoom
Precisão da função dentro de 0,1
32
2. Exemplos
35
2. Exemplos
5
1,8
1,6
Q
P
4
L(x)
1,4
3
1,2
1,0
2
8,00
8,10
8,20
8,30
8,40
8,50
8,60
8,70
8,80
Estimativa da coordenada x de Q pela aplicação de zoom
8,90
9,00
-1,5
-1,4
-1,3
-1,2
-1,1
-1,0
Estimativa da coordenada x de P pela aplicação de zoom
33
36
6
2. Exemplos
3. Diferenciais
3,0
L(x)
2,8
Q
2,6
2,4
2,2
3,5
3,7
3,9
4,1
4,3
4,5
Significado geométrico da diferencial
Estimativa da coordenada x de Q pela aplicação de zoom
37
3. Diferenciais
40
3. Diferenciais
As idéias por trás das aproximações lineares
são algumas vezes formuladas na terminologia pela
notação de diferenciais.
A inclinação da reta tangente PR é a
derivada f ’(x). Assim, a distância direta de S a R é
dy = f ’(x)dx.
Se y = f(x), onde f é uma função diferenciável, então a diferencial dx é uma variável
independente; isto é, a dx pode ser dado um valor
real qualquer. A diferencial dy é então definida em
termos de dx pela equação
Consequentemente, dy representa a distância que a reta tangente sobe ou desce (a variação
na linearização), enquanto ∆y representa a
distância que a curva y = f(x) sobe ou desce quando
x varia por uma quantidade dx.
dy = f ′( x )dx
38
3. Diferenciais
41
4. Exemplos
Exemplo 4: Compare os valores de ∆y e dy se
y = f(x) = x3 + x2 – 2x + 1 e x variar (a) de 2 para
Assim dy é uma variável dependente; ela
depende dos valores de x e dx. Se a dx for dado
um valor específico e x for algum número
específico no domínio de f, então o valor numérico
de dy está determinado.
2,05 e (b) de 2 para 2,01
O significado geométrico de diferenciais
está na figura a seguir. Seja P (x, f(x)) e
Q (x + ∆x, f(x + ∆x)) pontos sobre o gráfico de f e
façamos dx = ∆x. A variação correspondente em y
é
∆y = f ( x + ∆x ) − f ( x )
39
42
7
4. Exemplos
4. Exemplos
5
Em geral
4
dy = f ′( x )dx
3
2
(
0
-3
-2
-1
)
dy = 3 x 2 + 2 x − 2 dx
1
0
1
2
3
-1
Quando x = 2 e dx = ∆x = 0,05, temos
-2
-3
2
dy = 3 ( 2 ) + 2 ( 2 ) − 2  ⋅ 0,05 = 0,7


-4
-5
Gráfico da função f(x) = x3 + x2 - 2x + 1
43
4. Exemplos
46
4. Exemplos
18
(b)
f (2,01) = (2,01)3 + (2,01)2 − 2(2,01) + 1 = 9,140701
16
y = x 3 + x 2 - 2x + 1
∆y = f (2,01) − f (2) = 0,140701
14
12
∆y
dy
Quando x = 2 e dx = ∆x = 0,01, temos
10
(2, 9)
8
dy = 3 ( 2 ) + 2 ( 2 ) − 2 ⋅ 0,01 = 0,14


2
6
1,8
2,0
2,2
2,4
Zoom aplicado à função f(x) = x3 + x2 - 2x + 1
comparando dy e ∆ y quando a = 2 para ∆ x = dx = 0,4
2,6
44
4. Exemplos
47
4. Exemplos
Solução: (a) Temos que
Note que no Exemplo 4 a aproximação
∆y ≅ dy torna-se melhor à medida que ∆x fica
menor. Note também que é muito mais fácil
computar dy do que ∆y.
f (2) = 23 + 22 − 2(2) + 1 = 9
Para as funções mais complicadas pode ser
impossível computar exatamente ∆y. Nesses casos,
a aproximação por diferenciais é especialmente
proveitosa.
f (2,05) = (2,05)3 + (2,05)2 − 2(2,05) + 1 = 9,717625
∆y = f (2,05) − f (2) = 0,717625
45
48
8
4. Exemplos
4. Exemplos
Na notação de diferenciais, a aproximação
O próximo exemplo ilustra o uso de
diferenciais na estimativa de erros que ocorrem
em virtude de medidas aproximadas.
linear
∆y = f ( x + ∆x ) − f ( x )
pode ser escrita como
f (a + dx ) ≅ f (a ) + dy
fazendo x = a, ∆x = dx e ∆y ≅ dy
49
4. Exemplos
52
4. Exemplos
Por exemplo, para a função
Exemplo 5: O raio de uma esfera tem 21 cm, com
um erro de medida possível de no máximo 0,05 cm.
Qual é o erro máximo cometido ao usar esse valor
de raio para computar o volume da esfera?
f (x) = x + 3
do Exemplo 2, temos
dy = f ′( x )dx =
dx
2 x +3
50
4. Exemplos
53
4. Exemplos
Se a = 1 e dx = ∆x = 0,05, então
dy =
0,05
2 1+ 3
Solução: Se o raio da esfera for r, então o volume
é V = (4/3)πr3. Se o erro na medida do valor de r
for denotado por dr = ∆r, então o erro
correspondente no cálculo do valor de V é ∆V, que
pode ser aproximado pela diferencial
= 0,0125
e
dV = 4π r 2dr
4,05 = f (1,05) ≅ f (1) + dy = 2,0125
exatamente como encontramos no Exemplo 2
51
54
9
4. Exemplos
Quando r = 21 e dr = 0,05, temos
dV = 4π ⋅ (21)2 ⋅ 0,05 ≅ 277
O erro máximo no volume calculado é de
cerca de 277 cm3.
Sendo o volume aproximadamente igual a
38792 cm3, concluímos que o mesmo pode variar
entre
38792 − 277 < V < 38792 + 277
38515 cm3 < V < 39069 cm3
55
4. Exemplos
Nota: Embora o erro possível no Exemplo 5 possa
parecer muito grande, uma idéia melhor dele é
dada pelo erro relativo, que é computado
dividindo-se o erro pelo volume total
∆V dV 4π r 2dr
dr
≅
=
=3
4 3
V
V
r
πr
3
56
4. Exemplos
Assim, o erro relativo no volume é cerca de
três vezes o erro relativo no raio. No Exemplo 5 o
erro relativo no raio é de aproximadamente
dr/r = 0,05/21 ≅ 0,0024 e produz um erro relativo
de 0,0072 no volume.
Os erros também podem ser expressos
como erros percentuais de 0,24% no raio e 0,72%
no volume.
57
10