Prova 1 c/ soluções

Tópicos de eletromagnetismo 2/2010 – Prova 1 – Soluções
A C Tort∗
16 de Outubro de 2010
Problema 1 Lei de Gauss Um dodecaedro regular é um poliedro com doze iguais faces perfazendo uma área total área
total A. Suponha que uma carga q seja colocada no centro geométrico do dodecaedro.
(a) Calcule o fluxo do campo elétrico através de cada
face do dodecaedro.
(b) Suponha que o campo elétrico seja aproximadamente uniforme em cada face do dodecaedro e calcule seu valor.
(c) Calcule, aproximadamente, a magnitude da força eletrostática entre a carga q e uma carga de teste q0 no
centro de uma face do dodecaedro.
(d) Suponha que uma segunda carga q ′ seja colocada em
um ponto exterior ao dodecaedro. Determine o fluxo
do campo elétrico criado por q ′ através do dodecaedro.
(e) Suponha que esta segunda carga esteja a uma
distância perpendicular D do centro geométrico de
uma das faces. Qual será agora, aproximadamente,
a magnitude da força eletrostática sobre a carga de
teste q0 colocada no centro de uma face do dodecaedro.
Escreva as respostas em função dos dados do problema.
∗ email:
[email protected]
1
S OLUÇ ÃO 1 :
(a) Lei de Gauss:
q
,
ǫ0
⇒
Φface =
EA =
q
,
ǫ0
⇒
Φ=
(b)
Φ
q
.
=
12
12ǫ0
E=
(c)
F ≈ q0 E =
q
.
Aǫ0
q0 q
.
Aǫ0
(d)
Φ ′ = 0,
q ′ está colocada em um ponto exterior à superfı́cie gaussiana!
(e)
q0 q ′
q0 q .
−
F =
4πǫ0 d2
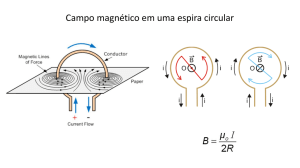
Aǫ0 Problema 2 Lei de Ampére A figura mostra uma espira condutora de raio R percorrida por uma corrente constante
i0 . Também são mostradas algumas linhas de forçado campo indução magnética B representativas.
(a) Qual o valor da circulação de B se o caminho de integração coincide com a linha de força denotada por a? E
se coincidir com a linha de força b?
(b) O campo B sobre o eixo Z perpendicular ao plano que contém a espira e que passa por seu centro é dado por:
B = Bz ẑ =
µ0 R2 i0
2 (R2 + z 2 )3/2
Calcule:
Z
+∞
Bz dz.
−∞
(c) Por que o caminho de volta pode ser ignorado?
2
ẑ.
a
x
b
S OLUÇ ÃO 2 :
(a) Pelo caminho fechado a a circulação de B vale µ0 I, e pelo caminho b, −µ0 I.
(b)
Z
+∞
Bz dz = µ0 i,
−∞
um resultado aparentemente conflitante com a lei de Ampère, pois o caminho não é fechado. O conflito é
resolvido no item seguinte.
(c) O caminho de volta passa pelo infinito, onde o campo é nulo.
Problema 3 Lei de Faraday A figura abaixo mostra uma espira perfeitamente condutora, R = 0, quadrada, de lado ℓ,
que se move da esquerda para a direita, parcialmente imersa em um campo magnético uniforme e constante perpendicular
ao plano da folha, apontando para dentro, descrito pela potencial vetorial A = (1/2)r × B. A espira tem indutância L. A
variável x(t) mede o quanto a espira está imersa no campo magnético no instante t.
⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗
x(t)
(a) Calcule o campo indução magnética B.
⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗
⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗
(c) Obtenha uma expressão para a corrente induzida na espira.
⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗
⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗
B
⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗
3
v(t)
ℓ
(b) Mostre que a espira descreve um movimento
harmônico simples.
S OLUÇ ÃO 3 :
(a)
x̂ ŷ
1 1
A = r × B = x y
2
2 0 0
Portanto:
(b) Solução padrão:
constante:
x̂
B = ∇ × A = ∂x
yBz
2
ẑ
z
Bz
1
= (yBz x̂ − xBz ŷ) .
2
ŷ
∂y
xBz
−
2
= −Bz ẑ.
Bz ẑ
∂z
como a espira é perfeitamente condutora, o fluxo magnético através da mesma deve ser
−Bℓx(t) + LI(t) = Φ0 .
onde Φ0 é uma constante. A força sobre a parte móvel do circuito é dada por:
F = −I(t) ℓB x̂.
A equação de movimento se escreve:
d2 x(t)
= −I(t)ℓB.
dt2
A corrente induzida I(t) pode ser escrita como:
m
Φ0
Bℓx(t)
+
.
L
L
Portanto, a equação de movimento pode ser rescrita como:
I(t)) =
d2 x(t)
Φ0 ℓB
ℓ2 B 2 x(t)
=
−
−
,
dt2
mL
mL
ou ainda:
Φ0 ℓB
d2 x(t) ℓ2 B 2 x(t)
+
=−
.
dt2
mL
mL
Este resultado é suficiente para mostrar que a espira descreve um M.H.S..
Solução alternativa:
Φ = −Bℓx(t) + LI(t) = constante.
Portanto, Φ̇ = 0. Segue que:
−B ℓ ẋ(t) + L I˙ = 0.
Convém mudar a notação: ẋ(t) ≡ v(t), logo:
4
v(t) =
L dI(t)
.
Bℓ dt
A força sobre a parte móvel do circuito é dada por:
F = −I(t) ℓB x̂,
e a equação de movimento permite escrever:
I(t) ℓB
dv(t)
=−
.
dt
m
Derivando uma vez mais em relação ao tempo:
d2 v(t)
ℓB dI(t)
ℓ2 B 2
=−
=−
L v(t).
2
dt
m dt
m
Ou ainda:
d2 v(t) ℓ2 B 2
+
v(t) = 0.
dt2
mL
Como a velocidade da espira obedece a uma equação de OHS, ela será senoidal. A posição x(t), que é a
integral de v(t), também será uma função senoidal, logo, o movimento da espira é harmônico simples. Se você
derivar a equação diferencial para x(t) mais uma vez obterá esta equação, isto mostra que as duas soluções são
equivalentes.
(c) A solução da equação diferencial para x(t) é dada por:
Φ0
+ C1 cos
x(t) =
ℓB
ℓB
√
t + C2 ,
mL
onde o termo constante é a solução particular e o cosseno, a solução da homogênea. As constantes C1 e C2
dependem das condições iniciais. A corrente pode ser obtida com, por exemplo, a relação:
I(t)) =
ℓB x(t)
Φ0
ℓB
Φ0
+
=2
+
C1 cos
L
L
L
L
5
ℓB
√
t + C2 .
mL