AGRUPAMENTO DE ESCOLAS DE MORTÁGUA
ESCOLA SECUNDÁRIA DR. JOÃO LOPES DE MORAIS - MORTÁGUA
Prova de Avaliação 5 – 12º ano – Matemática A – março de 2016
Esta prova é constituída por duas partes. Na 1ª parte apresente o seu raciocínio de forma clara, indicando os
cálculos efetuados e as justificações julgadas necessárias. Na 2ª parte em cada uma das questões selecione a
opção correta. Cada questão certa vale 9 pontos e cada questão errada, não respondida ou anulada 0 pontos.
Versão1
1ª PARTE
1) Admita que a concentração de um produto químico na água, em gramas por litro, t minutos após a sua
colocação na água, é dada, aproximadamente, por C( t ) 0,5t 2e0,1t , com t 0 .
Resolva os itens seguintes, recorrendo a métodos exclusivamente analíticos.
a) Calcule lim C( t ) e interprete o valor obtido no contexto do problema.
t
b) Determine o valor de t para o qual a concentração desse produto químico na água é máxima.
2)
Considere a função g, de domínio IR , definida por g( x )
1 ln x
.
x2
1 2 ln x
, estude a função g quanto ao sentido da concavidade e quanto à
x3
existência de pontos de inflexão, recorrendo a métodos analíticos, sem utilizar a calculadora.
Na sua resposta, deve indicar o(s) intervalo(s) de concavidade e, caso existam, os valores de x para
os quais a função g tem pontos de inflexão.
a) Sabendo que g '( x )
b) Considere, num referencial o.n. xOy, a representação gráfica da função g, os pontos A e B, e a reta
r de equação y m x , com m 0 .
Sabe-se que:
• os pontos A e B pertencem ao gráfico da função g;
• a abcissa do ponto A é o zero da função g;
• o ponto B é o ponto de intersecção da reta r com o gráfico da função g;
• a área do triângulo [OAB] é igual a 1.
Determine a abcissa do ponto B, recorrendo à calculadora gráfica e calcule o valor de m.
Na sua resposta, deve:
- equacionar o problema;
- reproduzir, num referencial, o gráfico da função ou os gráficos das funções visualizados,
devidamente identificados;
- indicar a abcissa do ponto A, a abcissa do ponto B e o valor de m com arredondamento às
centésimas.
www.arturrosa81.no.sapo.pt
1
[email protected]
x 2 e x 1
3) Seja f a função, de domínio IR, definida por f x
x 1
x ln x 3x
se x 0
se x 0
Sem recorrer à calculadora, a não ser para efetuar eventuais cálculos numéricos, resolva as alíneas
seguintes.
a) O gráfico da função f tem uma assíntota oblíqua quando x .
Determine a equação reduzida dessa assíntota.
b) Determine f 1 recorrendo à definição de derivada de uma função num ponto.
4) Seja f a função de domínio 0 , definida por f ( x ) 4sin(2 x ) 3 .
Recorrendo a métodos exclusivamente analíticos, resolva as alíneas seguintes.
a) Para um certo valor de tem-se sin(
3
5
) .
2
13
Determine o valor de f ( ) .
x
b) Considere a função g , de domínio 0 , , definida por g( x )
.
f ( x) 3
2
Estude a função g quanto à existência de assíntotas verticais do seu gráfico.
c) Na figura está representada em referencial o.n. a circunferência
de raio 4 e um trapézio [ABCD], com AD // BC .
O ponto A pertence ao eixo das abcissas, A, B e C pertencem à
circunferência e D=(-2,0).
c.1) Mostre que a área do trapézio é dada, em função de , por
A( ) 2 f ( ) 12sin 6 .
c.2) Obtenha a medida da amplitude do ângulo para a qual o
trapézio é retângulo em D.
www.arturrosa81.no.sapo.pt
2
[email protected]
2ª PARTE
1. Considere a função h , de domínio IR , e a reta de equação y 4 , assíntota do gráfico de h .
1
ln
2x
Qual é o valor de lim ?
x
h( x )
( A)
( B)
(C ) 4
( D) 0
2. Na figura 1, está representada, num referencial xOy, parte do gráfico de
uma função h '' , segunda derivada de uma função polinomial h .
Sabe-se que a primeira derivada da função h é nula no ponto de abcissa 0,
ou seja, h '(0) 0 .
y
h
O
x
Em qual das opções seguintes pode estar representada parte do gráfico da
função h ?
(A)
(B)
(C)
(D)
y
y
O
y
O
x
x
y
O
x
O
x
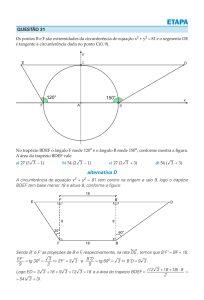
3. Na figura está representado um triângulo [ABC], retângulo em C.
Sejam BC a, AC b e AB c, com 1 a b c .
Qual é o valor de log b ( c a ) log b ( c a ) ?
( A) a c
( B ) 2b
(C ) 1
( D) 2
4. Na figura ao lado, estão representados, num referencial o. n. xOy,
uma circunferência e o triângulo [OAB]. Sabe-se que:
a circunferência tem centro no ponto O e raio 1;
A é o ponto de coordenadas (-1, 0)
B pertence à circunferência e tem ordenada negativa;
2
o ângulo AOB tem amplitude igual a
radianos.
3
Qual é a área do triângulo [OAB] ?
( A)
3
4
( B)
1
2
(C )
1
4
( D) 3
FIM
“A Natureza está escrita em linguagem Matemática.” Galileu Galilei (em italiano: Galileo Galilei; Pisa, 15 de fevereiro de 1564 – Florença, 8 de janeiro de
1642) foi físico, matemático, astrônomo e filósofo italiano.
www.arturrosa81.no.sapo.pt
3
[email protected]
www.arturrosa81.no.sapo.pt
4
[email protected]