Energia - Lógico Cursos Aliados

1. Na estratosfera, há um ciclo constante de criação e destruição do ozônio. A equação que
representa a destruição do ozônio pela ação da luz ultravioleta solar (UV) é:
UV
O3 
 O2  O
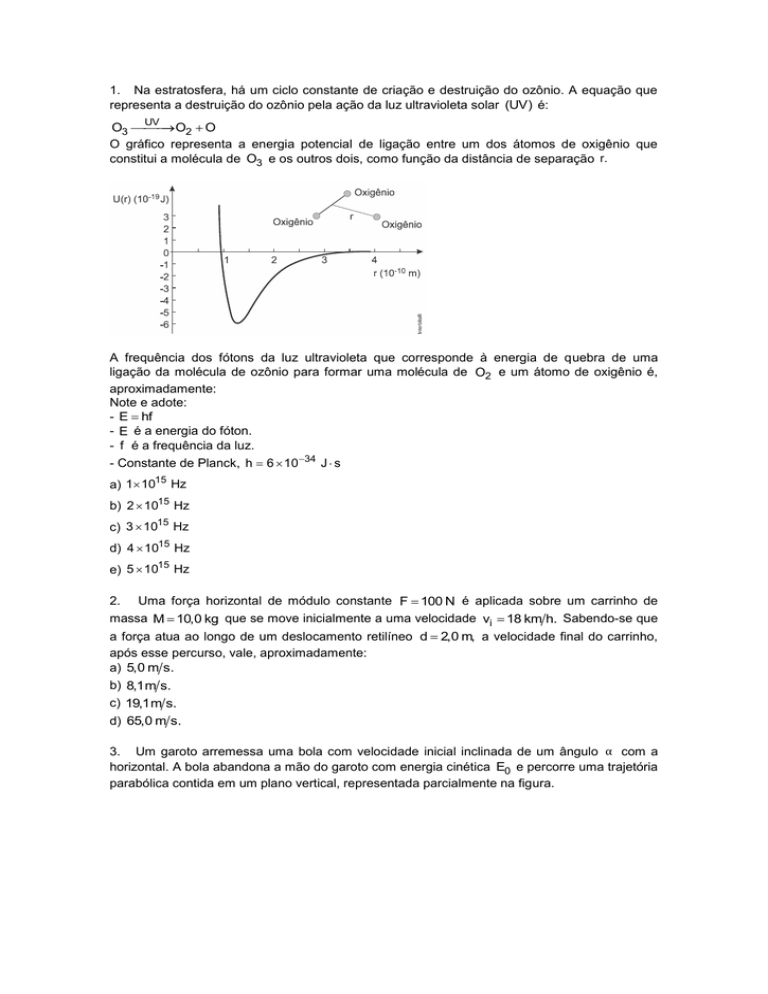
O gráfico representa a energia potencial de ligação entre um dos átomos de oxigênio que
constitui a molécula de O3 e os outros dois, como função da distância de separação r.
A frequência dos fótons da luz ultravioleta que corresponde à energia de quebra de uma
ligação da molécula de ozônio para formar uma molécula de O2 e um átomo de oxigênio é,
aproximadamente:
Note e adote:
- E  hf
- E é a energia do fóton.
- f é a frequência da luz.
- Constante de Planck, h  6  10 34 J  s
a) 1 1015 Hz
b) 2  1015 Hz
c) 3  1015 Hz
d) 4  1015 Hz
e) 5  1015 Hz
Uma força horizontal de módulo constante F  100 N é aplicada sobre um carrinho de
massa M  10,0 kg que se move inicialmente a uma velocidade vi  18 km h. Sabendo-se que
a força atua ao longo de um deslocamento retilíneo d  2,0 m, a velocidade final do carrinho,
após esse percurso, vale, aproximadamente:
a) 5,0 m s.
b) 8,1m s.
2.
c) 19,1m s.
d) 65,0 m s.
3. Um garoto arremessa uma bola com velocidade inicial inclinada de um ângulo α com a
horizontal. A bola abandona a mão do garoto com energia cinética E0 e percorre uma trajetória
parabólica contida em um plano vertical, representada parcialmente na figura.
Desprezando-se a resistência do ar, a energia cinética da bola no ponto mais alto de sua
trajetória é:
a) E0  sen α
b) E0  cos α
c) E0  cos2 α
d) E0  sen2 α
e)
E0  sen2 α
2
4. Uma pessoa arrasta uma caixa sobre uma superfície sem atrito de duas maneiras distintas,
conforme mostram as figuras (a) e (b). Nas duas situações, o módulo da força exercida pela
pessoa é igual e se mantém constante ao longo de um mesmo deslocamento.
Considerando a força F é correto afirmar que:
a) o trabalho realizado em (a) é igual ao trabalho realizado em (b).
b) o trabalho realizado em (a) é maior do que o trabalho realizado em (b).
c) o trabalho realizado em (a) é menor do que o trabalho realizado em (b).
d) não se pode comparar os trabalhos, porque não se conhece o valor da força.
5. Uma estrela de nêutrons é o objeto astrofísico mais denso que conhecemos, em que uma
massa maior que a massa do Sol ocupa uma região do espaço de apenas alguns quilômetros
de raio. Essas estrelas realizam um movimento de rotação, emitindo uma grande quantidade
de radiação eletromagnética a uma frequência bem definida. Quando detectamos uma estrela
de nêutrons através desse feixe de radiação, damos o nome a esse objeto de Pulsar.
Considere que um Pulsar foi detectado, e que o total de energia cinética relacionada com seu
movimento de rotação equivale a 2  10 42 J. Notou-se que, após um ano, o Pulsar perdeu
0,1% de sua energia cinética, principalmente em forma de radiação eletromagnética. A
potência irradiada pelo Pulsar vale: (Se necessário, utilize a aproximação 1 ano ~ 3,6  107 s.)
a) 7,2 10 46 W.
b) 2,0 1039 W.
c) 5,6 1031 W.
d) 1,8 1042 W.
6. Um automóvel viaja a uma velocidade constante v  90 km h em uma estrada plana e
retilínea. Sabendo-se que a resultante das forças de resistência ao movimento do automóvel
tem uma intensidade de 3,0 kN, a potência desenvolvida pelo motor é de:
a) 750 W.
b) 270 kW.
c) 75 kW.
d) 7,5 kW.
7. Helena, cuja massa é 50 kg, pratica o esporte radical bungee jumping. Em um treino, ela
se solta da beirada de um viaduto, com velocidade inicial nula, presa a uma faixa elástica de
comprimento natural L0  15 m e constante elástica k  250 N m.
Quando a faixa está esticada 10 m além de seu comprimento natural, o módulo da velocidade
de Helena é:
Note e adote:
- Aceleração da gravidade: 10 m s2 .
- A faixa é perfeitamente elástica; sua massa e efeitos dissipativos devem ser ignorados.
a) 0 m s
b) 5 m s
c) 10 m s
d) 15 m s
e) 20 m s
8. Uma bola de massa 10 g é solta de uma altura de 1,2 m a partir do repouso. A velocidade
da bola, imediatamente após colidir com o solo, é metade daquela registrada antes de colidir
com o solo. (Dados: g  10 m s2 e despreze a resistência do ar)
Calcule a energia dissipada pelo contato da bola com o solo, em mJ,
a) 30
b) 40
c) 60
d) 90
e) 120
9. No dia 15 de fevereiro de 2014, em Donetsk, na Ucrânia, o recorde mundial de salto com
vara foi quebrado por Renaud Lavillenie com a marca de 6,16 m. Nesse tipo de salto, o atleta
realiza uma corrida e utiliza uma vara para conseguir ultrapassar o “sarrafo” – termo utilizado
para se referir à barra horizontal suspensa, que deve ser ultrapassada no salto.
Considerando que ele ultrapassou o sarrafo com uma velocidade horizontal da ordem de
1cm s, fruto das transformações de energia ocorridas durante a prova, tem-se que, após
perder o contato com a vara, no ponto mais alto de sua trajetória, a energia mecânica
associada ao atleta era:
a) somente cinética
b) somente potencial elástica
c) somente potencial gravitacional
d) somente cinética e potencial gravitacional
e) cinética, potencial elástica e potencial gravitacional
10. Uma esfera de 5 kg cai de uma altura de 3,2 metros sobre um dispositivo provido de uma
mola de constante elástica 40 N m para amortecer sua queda, como mostra a figura.
Adotando g  10 m s2 e desprezando o atrito no sistema, pode-se afirmar que a velocidade
(v) que a esfera atinge o mecanismo, em m s e a contração da mola (x), em metros, valem:
a) v  8; x  2
b) v  16; x  2
c) v  8; x  2 2
d) v  16; x  2 2
11. Um sistema mecânico é utilizado para fazer uma força sobre uma mola, comprimindo-a.
Se essa força dobrar, a energia armazenada na mola:
a) cairá a um quarto.
b) cairá à metade.
c) permanecerá constante.
d) dobrará.
e) será quadruplicada.
12. O salto em distância é uma modalidade olímpica de atletismo em que os competidores
combinam velocidade, força e agilidade para saltarem o mais longe possível a partir de um
ponto pré-determinado. Sua origem remonta aos Jogos Olímpicos da Antiguidade. Nos Jogos
Olímpicos da Era Moderna ele é disputado no masculino desde a primeira edição, em Atenas
no ano de 1896, e no feminino desde os jogos de Londres, em 1948.
Foi apenas na 5ª edição das Paraolimpíadas, em Toronto (Canadá), em 1976, que atletas
amputados ou com comprometimento visual puderam participar pela primeira vez. Com isso, o
atletismo passou a contar com as modalidades de salto em distância e salto em altura.
A Física está presente no salto em distância, de forma simplificada, em quatro momentos:
1º momento: Antes de saltar o indivíduo corre por uma raia, flexiona as pernas, dando um
último passo, antes da linha que limita a área de corrida, que exerce uma força contra o chão.
Desta forma o atleta faz uso da Terceira Lei de Newton, e é a partir daí que executa o salto.
2º momento: A Segunda Lei de Newton nos deixa claro que, para uma mesma força, quanto
maior a massa corpórea do atleta menor sua aceleração, portanto, atletas com muita massa
saltarão, em princípio, uma menor distância, se não exercerem uma força maior sobre o chão,
quando ainda em contato com o mesmo.
3º momento: Durante a fase de voo do atleta ele é atraído pela força gravitacional e não há
nenhuma força na direção horizontal atuando sobre ele, considerando que a força de atrito com
o ar é muito pequena. No pouso, o local onde ele toca por último o solo é considerado a marca
para sua classificação (alcance horizontal).
4º momento: Chegando ao solo, o atleta ainda se desloca, deslizando por uma determinada
distância que irá depender da força de atrito entre a região de contato com o solo,
principalmente entre a sola da sua sapatilha e o pavimento que constitui o piso. No instante em
que o atleta para completamente, a resultante das forças sobre ele é nula.
Um bom atleta no salto em distância é também um bom corredor. Durante um tiro curto um
bom corredor pode atingir uma velocidade de 10 m s. Se um atleta, de 70 kg de massa, ao
partir do repouso, atinge essa velocidade no momento do salto, qual o trabalho realizado pela
força que impulsiona o atleta nesse intervalo, desprezando as forças internas do atleta?
a) 7.000 J.
b) 3.500 J.
c) 1.750 J.
d) 1.400 J.
13.
Um carro lançado pela indústria brasileira tem, aproximadamente, 1.500 kg e pode
acelerar do repouso até uma velocidade de 108 km h, em 10 s, em um terreno plano. Nesta
situação, é correto afirmar-se que a potência deste veículo vale:
a) 135 kW.
b) 16,875 kW.
c) 33,75 kW.
d) 100 kW.
e) 67,5 kW.
14. Considere que a cabine de um elevador despenque sem atrito em queda livre de uma
altura de 3 m, que corresponde aproximadamente a um andar. Considerando que a cabine
tenha massa de 500 kg e a aceleração da gravidade seja 10 m s2 , a energia cinética ao final
da queda será, em kJ,
a) 15.000.
b) 1.500.
c) 15.
d) 1,5.
15.
Na figura abaixo, está representada a trajetória de um projétil lançado no campo
gravitacional terrestre, com inclinação  em relação ao solo. A velocidade de lançamento é
v 0  v 0x  v0y , onde v 0x e v 0y são, respectivamente, as componentes horizontal e vertical
da velocidade v0 .
Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem
em que aparecem.
Considerando a energia potencial gravitacional igual a zero no solo e desprezando a
resistência do ar, as energias cinética e potencial do projétil, no ponto mais alto da trajetória,
valem, respectivamente, __________ e __________.
a) zero  mv 02 2
b) zero  mv 0x 2 2
c) mv02 2  mv0y2 2
d) mv0x2 2  mv0y2 2
e) mv0y2 2  mv0x2 2
16.
Em uma construção, um operário utiliza-se de uma roldana e gasta em média
5 segundos para erguer objetos do solo até uma laje, conforme mostra a figura abaixo.
Desprezando os atritos e considerando a gravidade local igual a 10 m s2 , pode-se afirmar que
a potência média e a força feita pelos braços do operário na execução da tarefa foram,
respectivamente, iguais a:
a) 300 W e 300 N.
b) 300 W e 150 N.
c) 300 W e 30 N.
d) 150 W e 300 N.
e) 150 W e 150 N.
17.
Um menino solta uma moeda, a partir do repouso, sobre um plano inclinado.
Desprezando-se o atrito, pode-se afirmar que a velocidade, ao final da rampa, é:
a) igual a de qualquer ponto anterior à do final.
b) diretamente proporcional à altura do plano.
c) diretamente proporcional ao quadrado da altura do plano.
d) diretamente proporciona à raiz quadrada da altura do plano.
e) inversamente proporcional à altura do plano.
18. Considere uma partícula que se desloca sobre o eixo horizontal x sob a ação de uma
força horizontal que varia com a posição x da partícula, de acordo com o gráfico representado.
Sabe-se que o tempo gasto pela partícula para chegar à posição x igual a 10,0 m é de 4,0 s.
Com base nessas informações, analise as afirmativas e marque com V as verdadeiras e com F,
as falsas.
( ) A partícula realiza um movimento uniforme entre as posições x  0 m e x  4,0 m.
(
) O trabalho realizado sobre a partícula entre as posições x  4,0 m e x  6,0 m é igual a
4,0 kJ.
(
) A potência média necessária para a partícula se deslocar de x  0 m até x  10,0 m é
igual a 4,0 kW.
) No intervalo entre x  6,0 m e x  10,0 m, a partícula desenvolveu uma velocidade
constante de módulo igual a 4,0 m s.
A alternativa que contém a sequência correta, de cima para baixo, é a:
a) F – V – V – F
b) F – F – V – V
c) F – V – F – V
d) V – F – V – V
e) V – V – F – F
(
19. O revezamento da tocha olímpica é um evento que ocorre desde os jogos de Berlim 1936.
Este rito é um retrato das cerimônias que um dia fizeram parte dos Jogos Olímpicos da
Antiguidade. Neste ano, nos Jogos Olímpicos Rio 2016, cerca de 12 mil condutores
percorrerão 329 cidades até o Rio de Janeiro. Considere que a tocha utilizada na cerimônia
tenha 1kg. Diante do exposto, assinale a alternativa que apresenta o módulo do trabalho
realizado pela força F3 de um condutor que levante a tocha e se desloque por 200 m na
horizontal (eixo x). Adote g  10 m s2 .
a) 2.400 J.
b) 800 J.
c) 2.050 J.
d) 0 J.
e) 900 J.
20. Em uma atividade experimental de física, foi proposto aos alunos que determinassem o
coeficiente de atrito dinâmico ou cinético e que também fizessem uma análise das grandezas
envolvidas nessa atividade. Tal atividade consistia em puxar um bloco de madeira sobre uma
superfície horizontal e plana com uma força F, com velocidade constante.
Sobre esta situação, pode-se inferir que:
a) o trabalho realizado pela força F é nulo.
b) o trabalho total realizado sobre o bloco é negativo.
c) o trabalho realizado pela força de atrito f é nulo.
d) o trabalho realizado pela força de atrito f é negativo.
e) o trabalho realizado pela força F é igual à variação da energia cinética do bloco.
21. A imagem abaixo é de uma cama hospitalar manual com três manivelas acopladas ao
leito, que permitem diversos tipos de elevações.
Com base na descrição do fabricante, determine o módulo aproximado da força, supostamente
constante, exercida por uma pessoa que desenvolve uma potência de 38,5 W, na extremidade
da manivela central, responsável pela elevação horizontal do leito, para que consiga elevar
uma pessoa com massa correspondente ao máximo suportado na especificação, desde a
altura mínima até a altura máxima. Sabe-se que cada volta completa, de perímetro igual a
1,8 m, corresponde a uma elevação de 70 mm.
a) 38,5 N
b) 42,8 N
c) 110,0 N
d) 385,0 N
22. Para realizar o levantamento de pesos de forma adequada, um halterofilista necessita
realizar 5 etapas, conforme mostrado a seguir.
Em um determinado campeonato mundial de levantamento de pesos, um atleta, com peso
corporal de 70 kg realizou um trabalho útil de 4,62 kJ para erguer uma barra com pesos
partindo da posição (I), chegando até a posição (V) e largando o peso no chão logo em
seguida. Partindo da posição (I) até chegar na posição (V), o atleta conseguiu erguer os pesos
a uma altura de 2,20m. (Considere a aceleração da gravidade com valor g  10 m s2 .)
Com base nessas informações, a relação entre o peso total erguido pelo atleta e o seu próprio
peso corporal é:
a) 5.
b) 1.
c) 2.
d) 4.
e) 3.
23. A usina de Itaipu é uma das maiores hidrelétricas do mundo em geração de energia. Com
20 unidades geradoras e 14.000 MW de potência total instalada, apresenta uma queda de
118,4 m e vazão nominal de 690 m3 s por unidade geradora. O cálculo da potência teórica
leva em conta a altura da massa de água represada pela barragem, a gravidade local
(10 m s2 ) e a densidade da água (1.000 kg m3 ). A diferença entre a potência teórica e a
instalada é a potência não aproveitada.
Qual e a potência, em MW, não aproveitada em cada unidade geradora de Itaipu?
a) 0
b) 1,18
c) 116,96
d) 816,96
e) 13.183,04
24. Uma campanha publicitária afirma que o veículo apresentado, de 1.450,0 kg, percorrendo
uma distância horizontal, a partir do repouso, atinge a velocidade de 108,0 km h em apenas
4,0 s. Desprezando as forças dissipativas e considerando g  10 m s2 , podemos afirmar que,
a potência média, em watts, desenvolvida pelo motor do veículo, neste intervalo de tempo é,
aproximadamente, igual a:
a) 1,47  105
b) 1,63  105
c) 3,26  105
d) 5,87  105
e) 6,52  105
25. Os gráficos da figura apresentam as evoluções da capacidade de atendimento e da
demanda máxima instantânea de energia elétrica em um país fictício no período de 2005 a
2015.
Analisando esses gráficos, pode-se inferir que:
a) de 2005 a 2008, a demanda máxima instantânea e a capacidade de atendimento
apresentaram valores compreendidos na faixa de 3.000 MW a 4.000 MW.
b) de 2005 a 2015, houve, pelo menos, um intervalo de um ano em que a capacidade de
atendimento apresentou decrescimento.
c) de 2005 a 2015, de ano a ano, a demanda máxima instantânea apresentou valores cada vez
maiores.
d) de 2008 a 2010, o crescimento da demanda máxima instantânea foi maior que o
crescimento da capacidade de atendimento.
e) de 2012 a 2015, a capacidade de atendimento variou mais de 1.000 MW.
26. Considere as seguintes situações: na primeira, o menino deixa cair a moeda, do ponto
mais alto, a partir do repouso, e a moeda chega à base do plano inclinado com uma energia
cinética Ec ; na segunda, do ponto mais alto, o menino lança a moeda ao longo do plano
inclinado para baixo, com velocidade V  2 m s, e ela, nessa segunda situação, chega a base
com uma energia cinética 20% maior do que na primeira situação.
Considerando-se a aceleração da gravidade g  10 m s2 , pode-se afirmar que a altura vertical,
em metros, desse plano é:
a) 1.
b) 1,5.
c) 2.
d) 2,5.
e) 3.
27. Um estudo realizado pela Embrapa Agrobiologia demonstrou que a produção do etanol de
cana-de-açúcar tem um balanço energético em torno de 9 : 1, o que significa que, para cada
unidade de energia fóssil consumida durante o processo produtivo, são geradas nove unidades
de energia renovável na forma de etanol. Sobre essa energia, é correto afirmar que houve,
durante o processo de produção do etanol,
a) conversão entre diversas formas de energia, principalmente química.
b) criação de energia química do etanol.
c) conversăo de energia térmica contida na cana-de-açúcar em energia química do etanol.
d) transformação de energia mecânica da cana-de-açúcar em energia térmica do etanol.
28.
Um bloco de massa igual a 10,0 kg se encontra preso na extremidade de uma mola de
constante elástica k igual a 10,0 N cm, conforme a figura. O bloco é puxado para uma posição
x0 igual a 6,0 cm para a direita da posição de equilíbrio e, em seguida, é abandonado do
repouso.
Nessas condições, é correto afirmar que a velocidade do bloco, ao passar pela posição de
equilíbrio, em m s, é igual a:
a) 0,65
b) 0,60
c) 0,55
d) 0,50
e) 0,45
29.
A figura abaixo mostra três objetos de massas m1, m2 e m3 , suspensos por fios
inextensíveis de massa desprezível que oscilam livremente. Os objetos 1 e 2 estão próximos
da superfície da Terra, onde a aceleração da gravidade é g, enquanto o objeto 3 está próximo
da superfície de um planeta onde a aceleração da gravidade é g / 2. Sejam h1, h2 e h3 as
alturas máximas atingidas pelos objetos 1, 2 e 3, respectivamente, em cada ciclo completo de
oscilação.
Sabendo-se que m1  3m2  m3 / 2 e que v1  v2  2v3 , a relação correta entre as alturas é
dada por:
a) h1  h2  h3.
b) h1  h2 e h1  h3 .
c) h1  h2 e h2  h3.
d) h1  h2 e h1  h3 .
30. Um marido sai do estádio de futebol após o jogo e resolve esticar a conversa com os
amigos em um bar. Às três da manhã, ele lembra que tinha prometido para a esposa chegar
em casa à meia-noite, porque é o horário em que ela costuma dormir. Ele correu para casa e
conseguiu fazer tudo que precisava em silêncio, para não acordá-la. Porém, no momento em
que foi deitar na cama, pronto para mentir no dia seguinte, que tinha chegado um pouco depois
da meia-noite, por descuido, esbarra o cotovelo no abajur do criado-mudo, que cai e quebra.
Se ele tivesse que culpar diretamente alguma forma de energia pela queda do abajur (que o
obrigou a dar explicações até o amanhecer), seria a energia:
a) potencial gravitacional.
b) interna.
c) potencial química.
d) potencial elástica.
e) potencial elétrica.
31. Em um experimento que valida a conservação da energia mecânica, um objeto de 4,0 kg
colide horizontalmente com uma mola relaxada, de constante elástica de 100 N / m. Esse
choque a comprime 1,6 cm. Qual é a velocidade, em m / s, desse objeto, antes de se chocar
com a mola?
a) 0,02
b) 0,40
c) 0,08
d) 0,13
32. Nanofibras produzidas a partir da mescla de dois polímeros (cujas siglas são PVDF e
PVDF-TrFE) estão ajudando na tecnologia de coletes à prova de balas. Tais coletes funcionam
absorvendo a energia do impacto da bala através de colisão inelástica. As nanofibras
conseguem absorver 98 Joules por grama, enquanto o tradicional material kevlar absorve 80
Joules por grama. Nessa condição, qual valor de energia cinética um projétil deve ter para que,
ao atingir um colete de nanofibra de 0,4 kg, ultrapasse em 300 Joules a capacidade total de
absorção de energia do colete?
a) 4.225 J
b) 13.145 J
c) 22.400 J
d) 27.700 J
e) 39.500 J
33.
No início de 2015, ocorreu a implementação do sistema de bandeiras tarifárias na
cobrança da energia elétrica. Atualmente, o sistema possui quatro bandeiras: Verde, Amarela,
Vermelha 1 e Vermelha 2. Estas tarifas estão relacionadas com o custo da produção de
eletricidade. Quando as hidrelétricas não são suficientes para suprir a demanda nacional de
eletricidade, em decorrência da escassez de chuvas, as termoelétricas são ligadas. O custo do
funcionamento das termoelétricas é maior, portanto, a conta paga pela população também se
torna maior. O quadro abaixo mostra as tarifas de cobrança, utilizando-se o sistema de
bandeiras tarifárias de 2016. Observe.
Bandeira
Verde
Amarela
Cobrança
Não há acréscimo na conta.
Acréscimo de R$ 1,50 para cada 100 kWh consumido.
Vermelha 1
Acréscimo de R$ 3,00 para cada 100 kWh consumido.
Vermelha 2
Acréscimo de R$ 4,50 para cada 100 kWh consumido.
Considere uma residência com 4 pessoas e que cada uma tome 2 banhos diários de 10
minutos. Assinale a alternativa que determina, em reais, o consumo da energia elétrica para
30 dias de bandeira Verde e para 30 dias de bandeira Vermelha 2 de um chuveiro de
5.500 W. Considere que a tarifa do sistema de distribuição convencional (sem acréscimo) seja
de R$ 0,20 por kWh.
a) R$ 44,00 e R$ 50,10.
b) R$ 35,00 e R$ 51,97.
c) R$ 43,00 e R$ 61,90.
d) R$ 20,00 e R$ 24,55.
e) R$ 44,00 e R$ 53,90.
34.
O Forno de Bier, um dos dispositivos mais antigos da termoterapia utilizados pela fisioterapia, é
assim denominado em homenagem ao seu inventor Dr. August Bier. É um compartimento que
se coloca por sobre a região a ser tratada, dentro do qual é gerado calor a partir de resistências
elétricas. Consiste em uma peça confeccionada com flandre e madeira, em forma de
semicilindro, aberto nas duas extremidades. Quando o paciente é introduzido no seu interior,
cobre-se o equipamento com um cobertor de flanela, para que haja um mínimo de perda de
calor do forno para o meio externo, através das aberturas existentes em suas extremidades.
Uma faixa de aplicação confiável fica em torno de 45 a 60 C. Para que o efeito terapêutico
seja atingido nos tecidos, é importante que o tempo de aplicação fique em torno de 20 a 30
minutos.
Se em uma clínica de fisioterapia são realizadas 10 aplicações diárias, de 30 minutos cada
uma, com o forno de Bier especificado acima em sua potência máxima, qual o custo mensal,
em reais, para essa clínica, devido ao uso desse aparelho, considerando-se 21 dias úteis e o
custo do kWh de R$ 0,20?
a) 31,50
b) 63,00
c) 157,50
d) 1.500,00
35.
Ótimos nadadores, os golfinhos conseguem saltar até 5 m acima do nível da água do
mar. Considere que um golfinho de 100 kg, inicialmente em repouso no ponto A, situado 3 m
abaixo da linha da água do mar, acione suas nadadeiras e atinja, no ponto B, determinada
velocidade, quando inicia o seu movimento ascendente e seu centro de massa descreve a
trajetória indicada na figura pela linha tracejada. Ao sair da água, seu centro de massa alcança
o ponto C, a uma altura de 5 m acima da linha da água, com módulo da velocidade igual a
4 10 m / s, conforme a figura.
Considere que, no trajeto de B para C, o golfinho perdeu 20% da energia cinética que tinha
ao chegar ao ponto B, devido à resistência imposta pela água ao seu movimento.
Desprezando a resistência do ar sobre o golfinho fora da água, a velocidade da água do mar e
adotando g  10 m / s2 , é correto afirmar que o módulo da quantidade de movimento adquirida
pelo golfinho no ponto B, em kg  m / s, é igual a:
a)
b)
c)
d)
e)
1.800.
2.000.
1.600.
1.000.
800.
36. Complete o quadro a seguir que explica as principais transformações de energia que
ocorre em cada tipo de usina.
Tipos de usinas
Hidrelétrica
Termoelétrica
Termonuclear
Eólica
Fotovoltaica
Energia inicial
I
II
III
IV
V
Energia final
Elétrica
Elétrica
Elétrica
Elétrica
Elétrica
A alternativa correta que completa a coluna energia inicial é:
a) I - térmica; II - térmica; III - térmica; IV - mecânica; V - luminosa.
b) I - mecânica; II - mecânica; III - luminosa; IV - mecânica; V - mecânica.
c) I - térmica; II - luminosa; III - luminosa; IV - mecânica; V - térmica.
d) I - mecânica; II - térmica; III - térmica; IV - mecânica; V - luminosa.
e) I - luminosa; II - térmica; III - mecânica; IV - mecânica; V - térmica.
37. Após uma cirurgia no ombro comumente o médico indica exercícios fisioterápicos para o
fortalecimento dos músculos. Esses, por sua vez, podem ser realizados com auxílio de alguns
equipamentos, como por exemplo: bolas, pesos e elásticos. Considere um exercício realizado
com a ajuda do elástico, em que o paciente deve puxá-lo até seu corpo e depois soltá-lo
lentamente.
A figura abaixo ilustra a posição do paciente.
Considerando o exposto, assinale a alternativa correta que completa as lacunas das frases a
seguir.
Quando o paciente puxa o elástico, fornece energia para este, que a armazena na forma de
__________. A força aplicada pelo elástico na mão do paciente é uma força __________ e
__________.
a) energia potencial elástica – constante – conservativa
b) energia potencial gravitacional – constante – não conservativa
c) energia potencial elástica – variável – conservativa
d) energia potencial gravitacional – variável – não conservativa
38. É possível relacionar o caos de um desastre natural com o fenômeno de um terremoto. O
sismógrafo vertical, representado na imagem a seguir, é um dos modelos utilizados para medir
a intensidade dos tremores.
A massa que está na ponta da haste tem 100 g, e o comprimento da haste, da ponta até o pivô
de articulação, é de 20 cm. Durante um tremor, a haste se move para baixo e isso causa um
π
rad entre a sua posição de equilíbrio e a nova posição.
6
π 1
Considerando que sen    , assinale a alternativa que apresenta, corretamente, a energia
6 2
despendida no processo.
a) 0,01J
b) 0,10 J
c) 1,10 J
d) 10,001J
e) 100,10 J
deslocamento de
Um elevador de 500 kg deve subir uma carga de 2,5 toneladas a uma altura de 20
metros, em um tempo inferior a 25 segundos. Qual deve ser a potência média mínima do
39.
motor do elevador, em kW ? (Dado: g  10 m / s2 )
a) 20
b) 16
c) 24
d) 38
e) 15
Um bloco de massa 5,00 kg é lançado sobre um plano inclinado do ponto A, com
velocidade inicial de 8,00 m / s, como indicado na figura abaixo.
40.
Considerando a aceleração da gravidade g  10,0 m / s2 , após percorrer 4,00 m, ele atinge o
repouso no ponto B. A energia dissipada pela força de atrito é:
a) 80,0J
b) 60,0J
c) 90,0J
d) 40,0J
e) 30,0J
41. SREC ou KERS (acrônimo de Sistema de Recuperação de Energia Cinética, em inglês
Kinetic Energy Recovery Systems) é um sistema de frenagem/travagem usado no mundo do
automobilismo, que recupera uma parte da energia cinética gerada pela desaceleração, em vez
de toda esta se perder na forma de calor. O método mais comum de armazenar energia é
acumular eletricidade em baterias ou em supercondensadores. Outro é guardar a energia
mecânica num sistema de volante de inércia.
O KERS é amplamente utilizado em carros de corrida da Fórmula 1. Em uma corrida, suponha
que um carro, de massa m  600kg, equipado com esse dispositivo, atinja ao final de uma reta
a velocidade máxima de 270km / h sem auxílio do KERS. Se o piloto desse carro tivesse
ativado o KERS, utilizando uma energia adicional acumulada no valor de 57% da energia de
uma desaceleração de 200km / h a 100km / h, qual seria a nova velocidade máxima atingida
na reta?
a) 282km / h
b) 290km / h
c) 300km / h
d) 384km / h
e) 424km / h
42. Um carro solar é um veículo que utiliza apenas a energia solar para a sua locomoção.
Tipicamente, o carro contém um painel fotovoltaico que converte a energia do Sol em energia
elétrica que, por sua vez, alimenta um motor elétrico. A imagem mostra o carro solar Tokai
Challenger, desenvolvido na Universidade de Tokai, no Japão, e que venceu o World Solar
Challenge de 2009, uma corrida internacional de carros solares, tendo atingido uma velocidade
média acima de 100 km h.
Considere uma região plana onde a insolação (energia solar por unidade de tempo e de área
que chega à superfície da Terra) seja de 1.000 W m2 , que o carro solar possua massa de
200 kg e seja construído de forma que o painel fotovoltaico em seu topo tenha uma área de
9,0 m2 e rendimento de 30%.
Desprezando as forças de resistência do ar, o tempo que esse carro solar levaria, a partir do
repouso, para atingir a velocidade de 108 km h é um valor mais próximo de:
a) 1,0 s.
b) 4,0 s.
c) 10 s.
d) 33 s.
e) 300 s.
43. Um pêndulo é formado por uma haste rígida inextensível de massa desprezível e em uma
das extremidades há uma esfera sólida de massa m. A outra extremidade é fixada em um
suporte horizontal. A haste tem comprimento L e a esfera tem raio r. O pêndulo é deslocado
da sua posição de equilíbrio de uma altura H e executa um movimento harmônico simples no
plano, conforme mostra a figura.
Com relação ao movimento desse pêndulo, analise as proposições.
I. A energia mecânica em A e B são iguais.
II. As energias cinética e potencial em A e B são iguais.
III. A energia cinética em A é mínima.
IV. A energia potencial em B é máxima.
Assinale a alternativa correta.
a) Somente as afirmativas I e II são verdadeiras.
b) Somente as afirmativas III e IV são verdadeiras.
c) Somente as afirmativas I e III são verdadeiras.
d) Somente as afirmativas I e IV são verdadeiras.
e) Todas afirmativas são verdadeiras.
44. A figura abaixo ilustra (fora de escala) o trecho de um brinquedo de parques de diversão,
que consiste em uma caixa onde duas pessoas entram e o conjunto desloca-se passando
pelos pontos A, B, C e D até atingir a mola no final do trajeto. Ao atingir e deformar a mola, o
conjunto entra momentaneamente em repouso e depois inverte o sentido do seu movimento,
retornando ao ponto de partida.
No exato instante em que o conjunto ( 2 pessoas + caixa) passa pelo ponto A, sua velocidade
é igual a VA  10 m s.
Considerando que o conjunto possui massa igual a 200 kg, qual é a deformação que a mola
ideal, de constante elástica 1100 N m, sofre quando o sistema atinge momentaneamente o
repouso? Utilize g  10 m s2 e despreze qualquer forma de atrito.
a) 3,7 m
b) 4,0 m
c) 4,3 m
d) 4,7 m
Gabarito:
Resposta
[A]
da
questão
1:
[Resposta do ponto de vista da disciplina de Física]
O gráfico mostra que a energia potencial de ligação tem valor mínimo, Emín  6  10 19 J.
Para quebrar a ligação, a energia potencial deve se tornar nula.
Emín (6  1019 )
Emín  hf  0  f 


f  1 1015 Hz.
h
6  1034
[Resposta do ponto de vista da disciplina de Química]
A energia de ligação ou dissociação da molécula é igual ao módulo da energia potencial na
separação de equilíbrio r0 :
E |U|
h f  |U|
6  10 34  f  6  10 19
f
6  10 19
6  10
34
 1 1015 Hz
Resposta
[B]
da
questão
2:
vi  18km h  5m s.
Supondo que a referida força seja a resultante, temos, pelo menos, duas soluções.
1ª Solução: Teorema da Energia Cinética.
m 2
10 2
WR  ΔEcin  F d 
v f  vi2  100  2 
v f  52  v f2  40  25 
2
2

v f  65 



v f  8,1m s.
2ª Solução: Princípio Fundamental e Equação de Torricelli.
Se a força é paralela ao deslocamento, a aceleração escalar ou tangencial tem módulo
constante e o movimento é uniformemente variado (MUV).
Aplicando o Princípio Fundamental da Dinâmica:
Fres  m a  100  10 a  a  10 m s2 .
Como o deslocamento é 2 m, aplicando a equação de Torricelli:
v 2f  vi2  2 a d  v 2f  5 2  2  10  2  65 
v f  8,1m s
Resposta
[C]
da
questão
m v 02
.
2
No ponto mais alto da trajetória a velocidade é: v x  v0 cos α.
A energia cinética ao abandonar a mão do garoto é: E0 
3:
(I)
m v 02
m v 2x m  v 0 cos α 
A energia cinética nesse ponto mais alto é: E 


 cos2 α.
2
2
2
2
Substituindo (I) em (II):
(II)
E  E0  cos2 α.
Resposta
[C]
da
questão
4:
Como o trabalho realizado na situação envolve translação na horizontal, sendo o deslocamento
igual em ambos os casos, terá maior trabalho realizado a situação que envolver a maior força
na direção horizontal. Como os módulos das forças são iguais nos dois casos, a primeira
situação, caso (a), tem uma redução da força na direção do deslocamento (horizontal) por ser
uma força inclinada, realizando menor trabalho no trecho. No caso (b) temos o maior trabalho
realizado, pois a força é aplicada na mesma direção do deslocamento.
Resposta
[C]
da
questão
5:
Observação: Fazendo as contas, de acordo com a aproximação sugerida, o ano teria 417
dias!
A energia perdida na forma de radiação (Er ) é:
Er  0,1% E 
0,1
 2  1042  E r  2  1039 J.
100
Calculando a potência irradiada:
Pr 
2  1039
3,6  10
7

Pr  5,6  1031 W.
Resposta
[C]
da
questão
6:
Se a velocidade é constante, a resultante das forças paralelas ao movimento é nula. Logo,
intensidade da força motriz (Fm ) é igual à intensidade da resultante das forças resistivas (Fr ).
Fm  Fr  3kN.
A velocidade é constante, v  90km h  25m s.
Aplicando a expressão de potência mecânica associada a uma força:
P  F v  3  25 
Resposta
[A]
P  75kW.
da
questão
7:
O plano de referência para energia potencial será adotado no ponto 25 m abaixo do ponto (A)
de onde Helena se solta.
Sendo a velocidade inicial nula, pela conservação da energia mecânica, tem-se:
A
Emec
 EB
mec  mg(L0  h) 
12.500  v 2  12.500 
Resposta
[D]
m v 2 kh2
50 v 2 250  102

 50  10  252 


2
2
2
2
v  0.
da
questão
8:
Ep  Ec
1
 m  v2
2
v  2gh
mgh 
Como a velocidade cai a metade após a colisão, a energia cinética final será
1
da energia
4
1
3
da energia foram perdidos.
 m  v 2 ). Logo,
2
4
3
3
3
ΔE   10  103  1,2  10  ΔE   120  103  ΔE   120 mJ  ΔE  90 mJ
4
4
4
inicial ( Ec 
Resposta
[D]
da
questão
9:
No ponto mais alto da trajetória, o atleta possuía velocidade 1cm s e estava a certa altura
1
6,16 m, ou seja, ele possui energia cinética Ec  m  v 2 e energia potencial Ep  m  g  h.
2
Resposta
[C]
da
questão
10:
Ec  Epgravitacional
1
m  v2  m  g  h
2
V  2gh
V  2  10  3,2
V 8m s
Ec  Epelástica
1
1
 m  v2   k  x2
2
2
m  v 2  k  x2
m  v2
x
k
x
5  64
x 8x2 2
40
Resposta
[E]
F  kx  x 
da
questão
11:
F
k
2 F  k  x  x 
2F
k
2
E
1
1 F
1 F2
2
k  x  E  k     E  
2
2 k 
2 k
E' 
1  2 F 
1
1 F2
F
k 
 E'  4   k     E'  4  
 E'  4  E

2  k 
2
2 k
k
2
Resposta
[B]
W  ΔEc  W 
Resposta
[E]
2
da
questão
12:
questão
13:
1
1
m  v 2  W   70  102  W  3.500 J
2
2
da
Dados: m  1.500 kg; V0  0 km h; V  108 km h  V  30 m s; Δt  10 s.
Essa questão pode ser resolvida de duas maneiras:
Lembrando que:
1
1
d  V0  Δt   a  Δt 2  d   a  Δt 2
2
2
Vem:
1ª opção:
P
W
Fd
mad
m  a  a  Δt 2
m  V 2  Δt
m  V2
P
P
P
P
P

Δt
Δt
Δt
2  Δt
2  Δt
2  Δt 2
P
1500  302
 P  67.500 W  P  67,5 kW
2  10
2ª opção:
W  ΔEc  W 
1
1
1
m  v 2f  m  vi2  W  m  v 2f  0
2
2
2
1
m  v 2f
m  v 2f
W
2
P
P
P
 P  67.500 W  P  67,5 kW
Δt
Δt
2  Δt
Resposta
[C]
da
questão
14:
1ª Solução:
Pela conservação da energia mecânica, a energia cinética ao final da queda é igual a energia
potencial no início da queda.
final
E cin
 E inicial
pot  mgh  500  10  3  15.000 J 
final
Ecin
 15kJ.
2ª Solução:
O movimento da cabine é uma queda livre. Pela equação de Torricelli:

v 2  v 02  2a ΔS  v 2  0  2  10  3  v 2  60(m  s) 2 .
final
Ecin

m v 2 500  60

 15.000 J 
2
2
Resposta
[D]
final
Ecin
 15 kJ.
da
questão
15:
Temos um lançamento oblíquo na qual podemos separar em dois movimentos independentes:
horizontalmente, um movimento retilíneo uniforme com velocidade constante de módulo
v0x  v0  cos φ e, verticalmente, um lançamento vertical com velocidade inicial igual a
v 0y  v 0  sen φ.
Para o ponto mais alto da trajetória a energia cinética está relacionada com a velocidade neste
ponto que é devida somente à componente horizontal, ou seja, v0x , logo:
Ec 
m  v 0x 2
2
Já a energia potencial no ponto mais alto será dada pela relação:
Epg  mgh
Mas essa energia pode ser relacionada à energia cinética inicial no lançamento vertical, por se
tratar de um sistema conservativo, então:
Epg  Ecy 
m  v0y 2
2
Resposta
[A]
da
Aplicando a definição de potência média:
Epot mgh 30  10  5
Pot 


 Pot  300 W.
Δt
Δt
5
Supondo que a subida tenha sido à velocidade constante:
F  P  mg  30  10 
F  300N.
questão
16:
Resposta
[D]
da
questão
17:
Pela conservação da energia mecânica:
mv 2
 m gh  v  2 gh  a velocidade é diretamente proporcional à raiz quadrada da altura
2
do plano inclinado.
Resposta
[A]
da
questão
18:
Observação: O enunciado deveria destacar que essa força é a resultante.
[F] Se a resultante é constante nesse intervalo, o movimento é uniformemente variado.
[V] O trabalho (W) realizado sobre a partícula é numericamente igual à área destacada no
gráfico, correspondente a esse intervalo.
6  4  4
W
 1000  W  4.000 J  W  4,0kJ.
2
[V] O trabalho realizado sobre a partícula de x  0 m até x  10,0 m é dado pela área
destacada no gráfico.
  6  4   4 10  6   2 
W

  1000  16.000 J.
2
2


Pm 
W 16000

 Pm  4.000 W 
Δt
4
Pm  4 kW.
[F] Como a resultante das forças atuantes é não nula, o movimento o movimento não pode ser
uniforme.
Resposta
[D]
da
questão
19:
Ao levantar a tocha o corredor exerce um trabalho nulo.
W  F  d  cos θ  W  F3  d  cos90  W  F3  d  0  W  0
Resposta
[D]
da
questão
20:
O trabalho da força de atrito é dado por: W  f ΔScos α, sendo α o ângulo entre a força e a
velocidade. No caso, α  180. Então:
W  f ΔS cos180  W   f ΔS (Trabalho negativo)
Resposta
[B]
da
questão
21:
questão
22:
Δy  y  y0
Δy  800  103  450  10 3  Δy  350  10 3
W  m  g  Δy  W  110  10  350  10 3  W  385 J
1 volta
70  103 m (elevação)
x voltas
350  103 m (elevação)
x  5 voltas
1 volta completa
1,8 m
5 voltas completas
d
d9m
W  Fd  F 
W
385

 42,8 N
d
9
Resposta
[E]
da
O peso do atleta é: Pa  70  10  700N.
O trabalho (W) realizado pelo atleta é transformado em energia potencial gravitacional para a
barra com os pesos. Calculando o peso do halteres (Ph ) :
W  Ph H  Ph 
W 4.620

 Ph  2.100N.
H
2,2
Fazendo a razão:
Ph
Pa

Ph
2.100

 3.
700
Pa
Resposta
[C]
da
questão
23:
A potência teórica (PT ) em cada unidade corresponde à energia potencial da água represada,
que tem vazão z 
V
 690 m3 s.
Δt
Sendo ρ a densidade da água, g a aceleração da gravidade e h a altura de queda, tem-se:
mgh ρ V gh
V

 ρ gh  PT  ρ z gh  103  690  10  118,4  816,96  106 W 
Δt
Δt
Δt
PT  816,96 MW.
PT 
A potência gerada em cada unidade é:
14.000
PG 
 PG  700 MW.
20
A potência não aproveitada (dissipada) corresponde à diferença entre a potência teórica e a
potência gerada.
Pd  PT  PG  816,96  700 
Resposta
[B]
Pd  116,96 MW.
da
questão
24:
A Potência média é dada pelo produto entre o módulo da força e a velocidade escalar média:
Δv
P  F  vm  F 
2
E pela segunda lei de Newton:
Δv
F  ma  m
Δt
Logo,
 Δv 
Δv Δv
P  m

P  m 
Δt 2
2 Δt
2
Então, substituindo os valores:
P  1450 kg 
Resposta
[D]
30 m / s2
2 4 s
 P  163.125 W  1,63  105 W
da
questão
25:
Observando o gráfico, vê-se que, no período de 2008 a 2010, a linha da demanda instantânea
máxima é mais íngreme que a linha da capacidade de atendimento. Isso mostra que houve um
maior crescimento da primeira em relação a segunda.
Resposta
[A]
da
questão
26:
Observação: o enunciado deveria especificar que o atrito entre o plano inclinado e a moeda é
desprezível.
Se o atrito é desprezível, pode-se aplicar a conservação da energia mecânica às duas
situações:
(I) : Ec  m g h
m V2

2
(I)
em
(II)

1,2
m
g
h

m
g
h



mV
2
(II) : 1,2 Ec  m g h 
2

0,2 g h 
Resposta
da
V2
22
 2h

2
2
h  1m.
questão
27:
[A]
A energia só pode ser transformada, jamais criada. Dito isto, a energia para transformação de
cana de açúcar num processo onde acontecerão diversos tipos de transformação
(especialmente energia química) tendo como produto final o etanol, energia armazenada
quimicamente (potencial). Desta forma, alternativa correta [A].
Resposta
[B]
da
questão
28:
Dados: k  10N/cm  103 N/m; x 0  6 cm  6  10 2 m; m  10kg.
Desprezando a ação de forças dissipativas, o sistema é conservativo. Então:
f
i
Emec
 Emec

2
m v 2 k x0

 v  x0
2
2
k
103
 6  10 2
 v  6  10 2  10  6  10 1 
m
10
v  0,6 m s.
Resposta
[D]
da
questão
29:
Pela conservação da energia mecânica:
fin
fin
Emec
 Emec
 m gh 
m v2
v2
 h
.
2
2g
Dessa expressão conclui-se que a altura máxima atingida depende apenas da velocidade
inicial e da intensidade do campo gravitacional local, não dependendo da massa.
Assim:

v2
h 1  1
2g

 v1  v 2  h1  h2 .


v 22
h 2 
2g

Para o objeto 3:
v1  2v3  v3 
v1
e a intensidade do campo gravitacional é g3  g 2.
2

v2
h 1  1
2g


2

 v1 
2



2
v
v2
h 3  3  
 1
2g3
4g

2 g
2


 
h1 v12 4 g


 h1  2h 3  h1  h 3 .
h3 2g v12
Concluindo:
h1  h 2 e h1  h3 .
Resposta
[A]
da
questão
30:
A energia potencial é definida como: Ep  m  g  h, e está diretamente relacionada com a altura
do objeto. E como o abajur caiu no chão e quebrou, o marido culpou a energia potencial
gravitacional.
Observação: a rigor ele também deveria culpar a energia cinética, uma vez que a energia
potencial gravitacional se transformou em energia cinética ao cair.
Resposta
[C]
da
questão
31:
Analisando o enunciado e utilizando os conhecimentos acerca de conservação de energia
mecânica, temos que:
Em  Em
i
f
Ec  Ep  Ec  Ep
i
i
f
f
2
m  vi
k  x2
0 0
2
2

4  vi2  100  1,6  102
vi 

100  1,6  102


2
2
4
vi  0,0064
vi  0,08 m s
Resposta
[E]
98 J
da
questão
32:
questão
33:
1g
xJ
400 g
x  39.200 J
Como ele quer um colete que ultrapasse 300 Joules, logo:
Ec  39.200  300  39.500 J
Resposta
[E]
da
4 pessoas  2 banhos  10 min  30 dias  2.400 min
Δt  2.400 min  40 h
P  5,5 kW
E  P  Δt  5,5 [kW]  40 [h]  E  220 kWh
1kWh
0,20 real
220 kWh x
x  44,00 reais
Na bandeira verde não possui acréscimo, logo custará R$ 44,00.
Na bandeira vermelha 2 possui acréscimo de R$ 4,50 pra cada 100 kWh consumido
100 kWh
4,5 reais
220 kWh
y  9,90 reais
y
Dessa forma, serão acrescentados R$ 9,90 na conta de R$ 44,00.
R$ 44,00  R$ 9,90  R$ 53,90.
Resposta
[A]
da
questão
34:
questão
35:
10 aplicações  30 min  300 min por dia
No mês : 300 min 21 dias  6300 min
1h
60min
xh
6300min
x  105h
E  P  Δt
E  1500 [W]  105 [h]
E  1,5 [kW]  105 [h]
E  157,5 kWh
1kWh
0,20
157,5
x
x  31,5 reais
Resposta
[B]
da
Dados: h BC  8m; vC  4 10 m/s; g  10 m/s2.
A energia mecânica no ponto C é 80% da energia mecânica no ponto B. Então, adotando
referencial de energia potencial no plano horizontal que contém o ponto B, vem:
C
E mec
 0,8E B
mec 
vB2
4

10

2
2
m vC
m vB2
 m gh BC  0,8
2
2
 2  10  0,8
0,8

320
0,8
 vB2 
2
vC
 2 gh BC
0,8

 vB  400  vB  20 m/s.
A quantidade de movimento no ponto B é, então:
QB  mvB  100  20 
Resposta
[D]
QB  2000 kg  m/s.
da
questão
36:
questão
37:
As transformações estão descritas na tabela.
Tipos de usinas
Energia inicial
Energia final
Hidrelétrica
I – Mecânica
Elétrica
Termoelétrica
II – Térmica
Elétrica
Termonuclear
III – Térmica
Elétrica
Eólica
IV – Mecânica
Elétrica
Fotovoltaica
V – Luminosa
Elétrica
Resposta
[C]
da
A energia armazenada no elástico é a energia potencial elástica, sendo uma força variável, de
acordo com a Lei de Hoocke e ainda conservativa.
Resposta
[B]
da
questão
38:
Usando a trigonometria:
sen /6 = h/0,2
h = 0,1 m.
Com o deslocamento vertical h podemos calcular a energia potencial gravitacional envolvida.
Ep = mgh  Ep = 0,1.10.0,1 = 0,10 J
Portanto, está correta a alternativa [B].
Resposta
[C]
da
questão
39:
No caso, a potência mínima será dada por:
P
 500  2500  kg  10 m / s2  20 m
τ mgh

P
 24000 W  24 kW
Δt
Δt
25 s
Resposta
[B]
da
questão
Nota: entendamos energia dissipada como energia mecânica dissipada.
A figura mostra a forças agindo sobre o bloco, bem como o deslocamento vertical (h):
sen30 
h
 1
 h  4    h  2 m.
4
 2
Aplicando o Teorema da Energia Cinética:
40:
WR  ΔEcin  W P  W N  W Fat 
 m gh  0  W Fat  0 
 5  2 10   W

Fat
E
dissip
  W Fat
m v 02

2
 5  8 2
 W Fat   60 J.
2

m v 2 m v 02


2
2
Edissip  60 J.
Resposta
[C]
da
questão
41:
Sem o KERS, para a velocidade de 270 km / h, temos:
2
m  v 2 600 kg   270 km / h 
 km 

 2,187  107 kg 

2
2
 h 
2
Einicial 
Energia da desaceleração de 200km / h a 100km / h, em módulo:
ΔE 
m 2
600
 v  v 02 
 1002  2002
2
2
 km 
ΔE  9  106 kg 

 h 
2
Reaproveitamento da energia de frenagem de 57% equivale a
2
 km 
 km 
6
Eker s  0,57  9  106 kg 
  5,13  10 kg  h 
h




2
Adicionando esta energia adicional à energia inicial:
2
2
 km 
 km 
 km 
6
7
Etotal  Einicial  Eker s  2,187  107 kg 
  5,13  10 kg  h   2,7  10 kg  h 
h






2
E a velocidade final atingida com o uso do KERS seria:
E
m  v2
v
2
2E
v
m
 km 
2  2,7  107 kg 

 h 
600 kg
2
v  300 km / h
Resposta
[D]
da
questão
42:
A intensidade de uma radiação é dada pela razão entre a potência total (PT ) captada e a área
de captação (A), como sugerem as unidades.
Dados: I  1.000 W/m2 ; A  9 m2 ; m  200 kg; v 0  0; v  108 km/h  30 m/s; η  30%.
I
PT
A
 PT  I A  1.000  9  PT  9.000 W.
Calculando a potência útil (PU) :
η
PU
 PU  30% PT  0,3  9.000  PU  2.700 W.
PT
A potência útil transfere energia cinética ao veículo.

m v 2  v02

2
Δt
PU 
 Δt 
Resposta
[C]

200 302  0

2  2.700

Δt  33,3 s.
da
questão
43:
Por tratar-se de uma MHS, pode-se dizer que há conservação de energia neste movimento.
Analisando as afirmativas, temos que:
[I] CORRETA. Devido a conservação de energia mecânica, a energia mecânica nos pontos A e
B são iguais.
[II] INCORRETA. É fácil observar que existe uma diferença de altura entre os pontos A e B.
Como Ep  m  g  h, onde h é a altura, a energia potencial nos dois pontos é diferente.
Sendo B o ponto mais baixo da trajetória, é direto observar que a energia potencial que existia
inicialmente no corpo é convertida em energia cinética. Desta forma, é possível dizer que neste
ponto tem-se que a energia cinética é máxima e a energia potencial é mínima.
Sendo A o ponto mais alto da trajetória, a energia potencial será máxima e a energia cinética
mínima.
[III] CORRETA. Ver explicação afirmativa [II].
[IV] INCORRETA. Ver explicação afirmativa [II].
Portanto, as afirmativas corretas são [I] e [III].
Resposta
[B]
da
questão
Em relação ao plano horizontal que passa por A, a altura em D é
HAB  1,6  1  0,6 m.
Usando a conservação da energia mecânica:
A
Emec
 ED
mec
200 10 
2
2

x  4 m.

m v 2A
k x2

 m g HAD
2
2
1.100 x 2
 200 10  0,6 
2

 x
10.000  1.200  2
1100

44: