Aula 39

MATEMÁTICA
8° ANO
ENSINO FUNDAMENTAL
PROF. IVAIR TAVEIRA
PROF.ª REGINA COSTA
CONTEÚDOS E HABILIDADES
Unidade IV
Trigonometria e área de figuras geométricas
2
CONTEÚDOS E HABILIDADES
Aula 39.2
Conteúdo
•• Revendo ortocentro e incentro.
3
CONTEÚDOS E HABILIDADES
Habilidade
•• Rever ortocentro e incentro através de exercícios de
fixação.
4
AULA
Alturas e Ortocentro
5
AULA
1. (CESESP-SP) Dentre os quatro centros principais de um
triângulo qualquer, há dois deles que podem se situar
no seu exterior, conforme o tipo de triângulo. Assinale a
alternativa em que os mesmos são citados.
a) O baricentro e o ortocentro.
b) O baricentro e o incentro.
c) O circuncentro e o incentro.
d) O circuncentro e o ortocentro.
e) O incentro e o ortocentro.
Resposta:
6
AULA
1. (CESESP-SP) Dentre os quatro centros principais de um
triângulo qualquer, há dois deles que podem se situar
no seu exterior, conforme o tipo de triângulo. Assinale a
alternativa em que os mesmos são citados.
a) O baricentro e o ortocentro.
b) O baricentro e o incentro.
c) O circuncentro e o incentro.
d) O circuncentro e o ortocentro.
e) O incentro e o ortocentro.
7
AULA
2. O segmento da perpendicular traçada de um vértice de
um triângulo à reta do lado oposto é denominada altura.
O ponto de intersecção das três retas suportes das
alturas do triângulo é chamado:
a) Baricentro
b) Incentro
c) Circuncentro
d) Ortocentro
e) Mediana
8
AULA
3. No triângulo ABC, da figura, AM e CN são medianas que
se interceptam em G. Sendo AG = 10 cm e CN = 18 cm,
calcule x, y e z.
9
DINÂMICA LOCAL INTERATIVA
Na figura abaixo, AH é altura. Calcule x e y:
10
AULA
O que é Incentro de um triângulo?
Incentro é o ponto de encontro das bissetrizes de um
triângulo.
1) O Incentro será ponto interior do triângulo.
2) O Incentro é o centro da circunferência inscrita ao
triângulo.
11
AULA
3) O Incentro é equidistante dos lados do triângulo.
Aplicação: No triângulo MTV, MH é a altura relativa ao lado
TV. Calcule os ângulos x e y do triângulo.
12
DINÂMICA LOCAL INTERATIVA
Na figura abaixo, AD é bissetriz. Calcule a e b:
B
13
RESUMO DO DIA
Bissetriz também é um
segmento de reta, com origem
em um dos vértices do triângulo
com a outra extremidade, no lado
oposto a esse vértice. Sendo
que ela divide ao meio o ângulo
correspondente ao vértice. Veja
o exemplo: AS é um segmento
de reta que dividiu o ângulo  em
duas partes iguais.
14
RESUMO DO DIA
Altura de um triângulo é um
segmento de reta perpendicular
a um lado do triângulo ou ao
seu prolongamento, traçado
pelo vértice oposto. Esse lado
é chamado base da altura, e o
ponto onde a altura encontra a
base é chamado de pé da altura.
15
RESUMO DO DIA
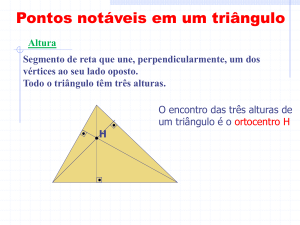
Alturas e Ortocentro
16
RESUMO DO DIA
O ortocentro é o ponto onde se
intersectam as 3 alturas relativas
de um triângulo, isto é, as
perpendiculares traçadas desde
os vértices até os lados opostos
(ou seus prolongamentos).
O nome deriva da expressão
grega orto, que quer dizer reto,
referindo-se ao ângulo formado
entre as bases e as alturas.
17
RESUMO DO DIA
Em um triângulo, o incentro (símbolo I) é o ponto em que as
suas três bissetrizes se cruzam, e fica à mesma distância
de todos os seus lados. Uma circunferência inscrita, ou
seja, interior ao triângulo e tangenciando os seus três lados,
tem como ponto central o incentro.
18
DESAFIO DO DIA
Na figura abaixo, determine os segmentos que representam
mediana, bissetriz e altura, sabendo que BP = PC e BÂN =
NÂC.
AH = ______________________
AN = ______________________
AP = ______________________
19