Lista de Exercícios-PRA - Estática RC Hibbeler

Lista de Exercícios-PRA - Estática
R. C. Hibbeler
I - Adição de forças vetoriais
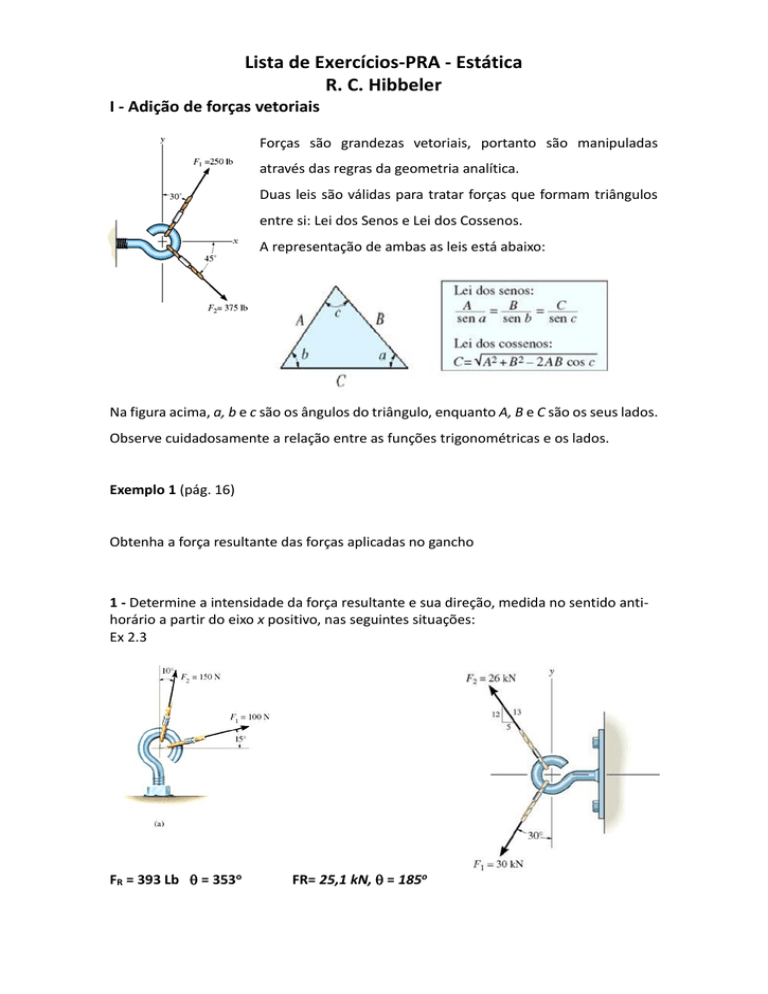
Forças são grandezas vetoriais, portanto são manipuladas
através das regras da geometria analítica.
Duas leis são válidas para tratar forças que formam triângulos
entre si: Lei dos Senos e Lei dos Cossenos.
A representação de ambas as leis está abaixo:
Na figura acima, a, b e c são os ângulos do triângulo, enquanto A, B e C são os seus lados.
Observe cuidadosamente a relação entre as funções trigonométricas e os lados.
Exemplo 1 (pág. 16)
Obtenha a força resultante das forças aplicadas no gancho
1 - Determine a intensidade da força resultante e sua direção, medida no sentido antihorário a partir do eixo x positivo, nas seguintes situações:
Ex 2.3
FR = 393 Lb  = 353o
FR= 25,1 kN,  = 185o
II - Decomposição de vetores em componentes
2 - Ex 2.38 - Determine a intensidade, a direção e sentido da
força resultante das três forças que atuam sobre o anel A.
Considere que F1 = 500 N e  = 20o .
R – FR = 1030,5 N  = 87,9o
3 – Encontre o valor do vetor força resultante do sistema, sua intensidade
(módulo) e sua direção.
FC = 70 N
FA = 90 N
26o
37o
FB = 150 N
R – FR = 172,93 N  = 26,5o
III –Vetores Cartesianos Tridimensionais
4 - Ex. 2.69 – A viga está sujeita às duas forças
mostradas. Expresse cada força na forma vetorial
cartesiana e determine a intensidade e os
ângulos
diretores coordenados da força
resultante.
5 - Exemplo 2.11 Duas forças atuam sobre o gancho mostrado na Figura abaixo.
Especifique os ângulos diretores coordenados de F2, de modo que a força resultante FR
atue ao longo do eixo positivo y e tenha intensidade de 800 N.
6 – Ex 2.61 Determine a intensidade e os ângulos
diretores coordenados da força F que atua sobre
a estaca.
IV - Vetores Posição
7 - 2.89 A chapa articulada é suportada pela corda AB. Se a força na corda for F = 340
lb, expresse essa força orientada de A para B e como um vetor cartesiano. Qual é o
comprimento da corda?
FAB = (-160i – 180j + 240 k ) lb
8 - 2.84 Expresse o vetor posição r na forma cartesiana; depois determine sua
intensidade e os ângulos diretores coordenados.
⃗ = (𝟒𝒊 + 𝟖𝒋 − 𝟖𝒌)𝒇𝒕 r = 12 ft  = 70,5º  = 48,2º  = 132º
𝒓
9 - 2.97 Os dois tratores puxam a árvore com as forças mostradas. Represente cada
força como um vetor cartesiano e determine a intensidade e os ângulos diretores
coordenados da força resultante.
FAB= (75,5i - 43,6j - 122k) lb FBC = ( 26,8i + 33,5j – 90,4k) lb
FR = 236 lb  = 64,3º  = 92,5º  = 154º
10 - 2.106 A torre é mantida reta pelos três cabos. Se a força em cada cabo que atua
sobre a torre for aquela mostrada na figura, determine a intensidade e os ângulos
diretores coordenados α, β, γ da força resultante. Considere que x = 20 m, y = 15m.
FR = 1,5 kN  = 77,6º  = 90,6º  = 168º
V - Produto Escalar
11 - 2.132 – Determine o ângulo  e a FAC projetada no eixo AO.
12 – 2.142 O cabo AB exerce uma forma de 80 N. Sobre a extremidade da barra de 3 m
de comprimento AO. Determine a intensidade da projeção dessa força ao longo da barra.
VI - Condição de equilíbrio de um Ponto Material

F  0
F
X
0 e
F
Y
0
13 – Exemplo 3.2 – Determine a tensão nos cabos AB e AD para o equilíbrio do motor
de 250 g mostrado na figura .
14 - Determine a força F exercida pelo homem no fio para manter o caixote na posição
mostrada na figura abaixo. Encontre,
também, a tração T no fio superior
(anterior à posição do gancho).
R-
15 - 3.35 - A mola tem rigidez K = 800 N/m e comprimento de 200 mm, sem deformação
. Determine a força nos cabos BC e BD quando a mola é mantida na posição mostrada.
R - FBD = 171 N FBC = 145 N
16 - 3.20 Determine as forças necessárias nos cabos AC e AB da figura para manter a
esfera D, de 20 kg, em equilíbrio . Suponha que F =
300 N e d = 1 m.
R – FAB = 98,7 N FAC = 267 N
VII - Sistemas de Forças Tridimensional
18 - 3.46 Considerando que o cabo AB esteja submetido a uma força de tração de 700
N, determine as força de tração nos cabos AC e AD e a intensidade da força vertical F.
O guincho é usado para puxar a rede de peixe de 200 kg para o píer. Determine a força
compressiva ao longo da barra AB e a tração no cabo do guincho DB. Considere a força
da barra CB de 2,52 kN e que a força em cada barra atua ao longo do seu eixo.
VIII - Momento de uma Força
19 - 4.10 – A chave inglesa é usada para soltar o parafuso. Determine o momento de
cada força em relação ao eixo do parafuso que passa através do ponto O.
M1 = 24,1 N.m
M2 = 14,5 N.m
20 – 4.22 Determine o momento de cada uma das três forças em relação ao ponto A.
Resolva o problema primeiro utilizando cada força com um todo e, depois, o princípio
dos momentos.
21 - 4.12 – Determine o momento no ponto A produzido pelas três forças agindo na
viga.
22 - Uma grua de construção recebe em seu cabo uma tração T = 30 k N. Ao puxar
uma carga da posição C. Calcule no instante da figura o momento produzido por
esta tração em relação à sua base em O.
Mo =( -341,04i + 392,32j – 208,8k ) N.m
23 - 4.80 - Se o momento de binário que atua
nos tubos tem intensidade de 400 N.m,
determine a intensidade F da força vertical
aplicada em cada chave.
IX– Sistema Equivalente e Carga Distribuída
A primeira equação estabelece que a força resultante do sistema é equivalente a soma
de todas as forças, enquanto a segunda indica que o momento da força resultante em
relação ao O (MRo) é igual a soma de todos os momento binários (MC) no sistema mais
os momentos de todas as forças no sistema em relação a O (MO).
FR = F
MRo= MC + MO
24 - 4.113 – Substitua as três forças atuantes no cano por uma única força resultante.
Especifique onde a força atua, tomando a extremidade A como referência.
25 - O material granuloso provoca o carregamento, distribuído sobre a viga como
mostrado na figura abaixo. Determine a intensidade e a localização da força resultante
do material granuloso.
500 N/m
200 N/m
4m
26 - 4.148 – Substitua o carregamento distribuído por uma única força resultante e
especifique a sua localização medida a partir do ponto A.
X - Equilíbrio de um Corpo Rígido
27 - A estante sustenta o motor elétrico da figura, que tem massa de 15 kg e centro de
massa em Gm. A plataforma tem massa 4 kg e centro de massa em GP. Supondo que um
único parafuso B prenda o suporte na parede lisa em A, determine a força normal em A
e os componentes horizontal e vertical da reação do parafuso no suporte.
28 - 5.32 12ª Ed A grua é sustentada por um pino em
C e um cabo AB. Se uma carga possui uma massa de
2t com seu centro de massa localizado em G,
determine as componentes horizontal e vertical da
reação no pino C e a força desenvolvida no cabo AB
sobre a grua quando x = 5 m.
29 - 5.25 – 12ª Ed – O transformador elétrico de 1.500 N
com centro de gravidade em G é sustentado por um pino
em A e uma sapata lisa em B. Determine as componentes
horizontal e vertical da reação no pino A e a reação da
sapata B sobre o transformador.
XI - Reações de Apoio
Nos exercícios 01 à 05 encontrar as reações de apoio nos pontos A e B das vigas Bi
apoiadas.
Ex 01 RhA = 0 RvA = 20 kN M = - 30 kN/m
Ex 02
Resposta:
RA = 40 kN
RB = 20 kN
Ex 03
Resposta:
RA = 60 kN
RB = 20 kN
Ex 04
Resposta:
RA = 12 kN
RB = 28 kN
Resposta:
RA = 12 kN
RB = 28 kN
Ex 05
Resposta:
RA = 46 kN
RB = 64 kN
XII - Treliça
Exemplo 6.1 – Determine a força em cada elemento da treliça mostrado na figura abaixo
e indique se os elementos estão sob tração ou compressão.
AX = 500 N AY = 500 N CY = 500 N FCA = 500 N
FBA = 500 N
FCB = 701,N
Exemplo - Calcule as componentes horizontais e
verticais da reação e determine a força em cada
elemento da treliça.
EX = 600 N EY = 200 N AY = 600 N
FAC = 750 N FAD = 450 N FDC = 250 N FDE
= 200 N FCE = 600 N FCD = 450 N
Ex01 - Utilizando o método dos nós, determine o esforço instalado em cada uma das
barras da treliça representada abaixo.
BX = 1,8 kN BY = 960 N CY = 3,36 kN
FBA = 1,2 kN FBC = 2,52 kN FCA =
3,36 kN FCD = 2,52 kN FDA = 3,48 kN