Física 1 Mecânica Instituto de Física

Física 1
Mecânica
Sandra Amato
Instituto de Física - UFRJ
Cinemática Unidimensional
1/ 45
(Cinemática)
Física 1
1 / 45
Outline
1
Referencial
2
Movimento Uniforme
3
Movimento Acelerado
4
Derivada
5
MRUV
6
Integral
7
Queda Livre
8
Exercícios
2/ 45
(Cinemática)
Física 1
2 / 45
Cinemática
Para descrever o movimento precisamos primeiramente escolher um referencial
(observador), que será representado aqui pelos eixos cartesianos. Devemos
também escolher a origem.
Descrever o movimento significa dizer em que posição o objeto estará em
qualquer instante de tempo, queremos determinar o vetor posição r t .
O vetor r t pode ser escrito em termos de suas componentes:
r t
x t
y t
z t k
3/ 45
(Cinemática)
Física 1
3 / 45
Chamamos de vetor deslocamento da partícula entre os instantes t1 e t2 o
vetor
r
r t2
r t1
x2
x1
y2
y1
z2
z1 k
e definimos o vetor velocidade média como a razão entre o vetor
deslocamento e o intervalo de tempo necessário para realizar o deslocamento
r
t
vmed t1 t2
r2 r1
t2 t1
Qual é a direção do vetor vmed t1 t2 ?
4/ 45
(Cinemática)
Física 1
4 / 45
Movimento Uniforme
O Movimento Uniforme se caracteriza pelo fato de que
percursos iguais ( r ) são realizados em intervalos de tempos
r
iguais. Pela definicão de velocidade vmed t1 t2
vemos que
t
ela não varia:
v t
v0
Como r v0 t ‹ r é um vetor constante ‹ Movimento
Retilíneo.
Sabendo o vetor posição em um instante inicial, r t0 , e a
velocidade v0 , podemos obter o vetor posição em qualquer
instante de tempo:
r
r t
r t0
v
v0
t
t t0
r t
(Cinemática)
r t0
Física 1
v0 t
t0
5/ 45
5 / 45
Movimento Uniforme
Lei Horária do MRU
r t
r t0
v0 t
t0
Como o movimento é retilíneo, é conveniente escolher a direção
de um dos eixos coincidente com a direção do movimento:
v0
v0
r t
como x t
r t
x t
x0
x0
v0 t
v0 t
t0
t0
6/ 45
(Cinemática)
Física 1
6 / 45
Gráficos - MU
Uma forma bastante prática de se visualizar o movimento é
através de gráficos
Gree
Graficamente, a velocidade é o coeficiente angular da reta no
gráfico x t
7/ 45
(Cinemática)
Física 1
7 / 45
Gráficos - MU
Como v
x
t
x2 x1
,
t2 t1
Podemos ter velocidades positivas ou negativas:
Se x2
x1 ‹ movimento no sentido crescente de x ‹ v
Se x2
x1 ‹ movimento no sentido decrescente de x ‹ v
Como ficaria o gráfico x
0
0
t ?
Quanto maior a inclinação maior a velocidade.
8/ 45
(Cinemática)
Física 1
8 / 45
Movimento Acelerado (ainda retilíneo)
Qualquer Movimento Retilíneo que não seja uniforme
(v constante) é chamado acelerado.
x
Da definição de vm
vemos que, graficamente, ela representa
t
o coeficiente angular da corda que liga os extremos P1 e P2 da
curva no gráfico x t .
A velocidade média entre t1 e t2 é equivalente à velocidade de um
movimento uniforme de uma partícula que saindo de x1 em t1
9/ 45
chegasse em x2 no instante t2 .
(Cinemática)
Física 1
9 / 45
Exemplo
Um carro percorre 10 km a 50 km/h até que a gasolina acaba. O
motorista caminha então 4 km em meia hora até um posto.
a) Qual a velocidade média desde que entrou no carro até o
posto?
b) Se, depois disso, o motorista traz o combustível de volta em
35 min, qual a velocidade média desde o instante em que entrou
no carro até o retorno ao posto?
c) Faça o gráfico da posição x em função do tempo.
10/ 45
(Cinemática)
Física 1
10 / 45
Tr
Daft
=
←
at
tueho
1
tech
2
bktot
Btr
Dttot
I
=
!
=
so
=
,
Dtz
0,2k
=
0,2+0,5
=
e
Dtz
+
,
Dye
=
I
Bt
J
e
km
4
lot
=
=
ki
Dkz
Sabena
:
Dttot
D
sabemos
;
h
0,7
i
kmlh
0,7
Note
I
a
que
das
union
±
velocidades
V
,
Vz
t
2-
2
I
Dktot
=
=
÷
DR
At
be
Dttot
=
0.7
(Cinemática)
+
0.58
,
,
+
D
+
=
e
kz
+
Dtz
+
z
8h
.
8
got
=
-
A
k
=
Zq
D
)
Bt }
→
Física 1
I
rkz
=
=
I.
D
-
=
k
7 's
}
hlh
11/ 45
11 / 45
Movimento Acelerado
Suponha que um carro percorra 400km em linha reta em 10
horas. ‹ vm 40km h.
Essa informação descreve bem o movimento?
‹ Precisamos do conceito de velocidade instantânea
12/ 45
(Cinemática)
Física 1
12 / 45
Velocidade Instantânea
A velocidade média dá apenas uma noção de como a partícula se desloca num
dado intervalo de tempo, porém se quisermos uma informação mais precisa
temos que definir a velocidade instantânea da partícula, no instante t ,
como sendo o limite da razão entre x e t quando t
0.
v t
lim
t
0
x
t
lim
t
x t
0
t
x t
t
dx
dt
Lê-se: A velocidade instantânea no instante t é a derivada da posição em
relação ao tempo neste instante.
13/ 45
(Cinemática)
Física 1
13 / 45
Velocidade Instantânea
Se mantivermos o ponto P fixo e considerarmos intervalos de
tempo cada vez menores, vemos que a direção da secante entre os
dois instantes de tempo, vai se aproximando à direção da
tangente no instante t
A velocidade instantânea é o coeficiente angular da reta tangente
à curva do gráfico x t .
14/ 45
(Cinemática)
Física 1
14 / 45
Exemplo
Uma pedra é lançada do topo de um prédio. Suponha que a
função posição seja dada por x t
5t 2 , onde x está em metros e
t em segundos. A origem do eixo x está no topo do prédio e seu
sentido positivo é para baixo. Determine a velocidade da pedra
em função do tempo durante o qual ela está caindo.
15/ 45
(Cinemática)
Física 1
15 / 45
Exemplo
16/ 45
(Cinemática)
Física 1
16 / 45
Gráfico
Podemos obter o gráfico de v
t a partir do gráfico x
t.
17/ 45
(Cinemática)
Física 1
17 / 45
Propriedades das Derivadas
A Derivada de uma função constante é nula.
x t
4
dx
x t1
x t0
4 4
lim
lim
0
t 0
t 0 t1
dt
t1 t0
t0
A derivada da função que é igual à variável independente t é
igual a 1.
x t
dx
dt
lim
t
0
x t1
t1
x t0
t0
t
lim
t
t1
0 t1
t0
t0
1
18/ 45
(Cinemática)
Física 1
18 / 45
Propriedades das Derivadas
A Derivada da função t n , é nt n
t2
x t
dx
dt
x t
dx
dt
1
t4
t
x t
t
t
2
t
lim
t
2
2
2t t
2t t
2t
t
0
t4
t
t
0
t
x t
x t
x t
lim
t
1
dx
dt
dx
dt
4
4t 3
4t
5
4
t5
19/ 45
(Cinemática)
Física 1
19 / 45
Propriedades das Derivadas
A Derivada das somas das funções é igual à soma das
derivadas
x t
t3
t2
t
5
dx
3t 2 2t 1 0
dt
A Derivada de at n , onde a é uma constante, é ant n
x t
x t
6t 2
3t 2
dx
dt
6t
3t 3
dx
dt
12t
1
9t 2
20/ 45
(Cinemática)
Física 1
20 / 45
Exemplo
Uma partícula move-se ao longo do eixo x de modo que sua
posição varia com o tempo de acordo com
x t
8
9t
2t 3
(posição em m e tempo em s)
a) Escreva o vetor posição da partícula em qualquer instante de
tempo. E no instante t 2s.
b) Qual a velocidade da partícula em qualquer instante de
tempo? E no instante t 3s?
21/ 45
(Cinemática)
Física 1
21 / 45
a)
X (
b
)
t=2s
)
(8
=
Flt
)
(
Fe
posiyao
with
l8
+
)
t
ie
-
DI
=
)
I
=
Ict
v.
(
9
=
)
t
=3
(
s
)
T
to
m
I
dt
6+2
-
=
.
D=
=
dt
D=
=(8t9t 2t3
) I
sect
=
9
=
-
6+2 )
I
(9-54)
i
=
-
45
i
ms
)
i
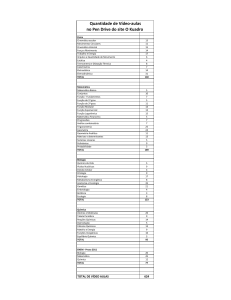
Exercícios
1
Uma partícula se move ao longo do eixo x de acordo com
x 50t 10t 2 (x em m, t em s). Obtenha:
1
2
3
4
2
A vm durante os 3 primeiros segundos
A velocidade instantânea v em t 3s
Faça o gráfico x t e indique como a vm e a v podem ser obtidas
Faça o gráfico v t
O gráfico abaixo representa o movimento de um automóvel
em uma estrada retilínea. Esboce o gráfico v t
correspondente e indique os intervalos em que ele se move (a)
para a frente, (b) para trás e (c) o intervalo em que está parado
22/ 45
(Cinemática)
Física 1
22 / 45
se
To
50£
=
-
D=
=
]
?
lot
-1
k(3)-k(=
50×3+10×325
=
=
t
VI.
b)
3
=
80
3
0
Is
-
D=
v=
-
=
50
+
Lot
dt
OCT
=3
)
=
50+60
=
110
-
Is
3
Aceleração
Uma outra grandeza importante no estudo da cinemática é a
aceleração, que descreve como a velocidade varia com o tempo.
Definimos a aceleração média
am t1 t2
v
t
v2
t2
v t
t
v1
t1
e a aceleração instantânea
a
lim
t
0
v
t
lim
t
0
v t
t
dv
dt
Aceleração instantânea é a derivada da velocidade em
relação ao tempo
dv
a
dt
23/ 45
(Cinemática)
Física 1
23 / 45
Aceleração
Como v
dx
dt
‹a
dv
dt
d
dt
d 2x
dt 2
dx
dt
Aceleração instantânea é a derivada segunda da posição em
relação ao tempo
d 2x
a
dt 2
Ex: Uma partícula move-se ao longo do eixo x de modo que sua
posição varia com o tempo de acordo com
x t
t3
27t
4
(posição em m e tempo em s) . Qual a aceleração em t
Em que instante a velocidade é nula?
2 s?
24/ 45
(Cinemática)
Física 1
24 / 45
Aceleração - através do gráfico v
t
25/ 45
(Cinemática)
Física 1
25 / 45
Gráfico da aceleração através do gráfico v
t
26/ 45
(Cinemática)
Física 1
26 / 45
Caso Particular - Aceleração Constante - MRUV
Aceleração instantânea é igual à aceleração média ‹ Gráfico
v t é uma reta.
a
v
t
escolhendo t1
0 e v1
v0 temos a
v v0
t 0
Equação da velocidade para o MRUV
v
Verifique que
dv
dt
v0
at
a
27/ 45
(Cinemática)
Física 1
27 / 45
MRUV - Variação da posição em função de t
v
x
t
‹x
x0
vt
v0 v
2
Como a é constante ‹ v
Substituindo v
v
v0 v0 at
2
v0
2v0 at
2
(Demonstre)
at nessa:
1
at
2
v0
Substituindo na eq. para x
Equação horária do MRUV
x
x0
v0 t
1 2
at
2
28/ 45
(Cinemática)
Física 1
28 / 45
MRUV
Equações fundamentais do MRUV
1 2
x x0 v0 t
at
2
v
v0
at
Eliminando o tempo entre elas, obtemos a chamada equação de
Torricelli
v2
v02
2a x
que permite determinar, o módulo da velocidade ao fim de um
deslocamento, a partir apenas do módulo da velocidade no início
do deslocamento, sem saber o tempo decorrido.
29/ 45
(Cinemática)
Física 1
29 / 45
Gráficos do MRUV
x
x0
v0 t
1
at 2
2
‹ O gráfico x
t é uma parábola.
30/ 45
(Cinemática)
Física 1
30 / 45
31/ 45
(Cinemática)
Física 1
31 / 45
Exercícios
Um motorista freia seu carro uniformemente de forma que a
velocidade cai de 60
72km/h para 30
6 km/h em 5s. Que
an
distância o carro percorrerá depois disso até parar? Quanto
tempo levará para percorrer essa distância adicional?
os
32/ 45
(Cinemática)
Física 1
32 / 45
O
H
movimentoeimniformementeacelenado.pohantovalemaseqnae.oisiz@oe-xotvotttgateDv-votatDooos.t
20
25
5s
.
.
v.
=
-
=
=
V
km/h
36
10
.
~
Is
.
72km/h
msondo
10
I
=
=
10
-
Podemos
10
O
=
-
mlsdq
2
-
parar
:
Torricelli
2
saber
10
=
V=o
-
para
a
ati
11
@
.
⇒
risen
z
D=
5
a
instant
deste
Vo
eng
a
+
⇒
memos
tempo
o
2
Dk
2
"
v2=
:
t
⇒
t
.
.
of
so
+
Dx
=
Doe
.
my
@
5sq
33/ 45
(Cinemática)
Física 1
33 / 45
Queda Livre
Um exemplo bastante comum de MRUV é a queda livre de uma
partícula próxima à superfície da Terra.
Esse é o movimento de uma partícula com velocidade inicial
vertical; ela realiza um movimento retilíneo com aceleração
constante apontando para baixo e de módulo g 9 8 m s 2 (em
boa aproximação).
Portanto, escolhendo como eixo do movimento, um eixo vertical
OY apontando para cima, obtemos ay
g, de modo que as
equações fundamentais da queda livre são
Equações de queda livre
y
y0
v0y t
1 2
gt
2
vy
v0y
gt
37/ 45
(Cinemática)
Física 1
37 / 45
38/ 45
(Cinemática)
Física 1
38 / 45
39/ 45
(Cinemática)
Física 1
39 / 45
Exercícios
H 2.54 Quando a luz verde de um sinal de trânsito acende, um
carro parte com aceleração constante a 2 2 m/s2 . No mesmo
instante, um caminhão, com velocidade constante de 9,5 m/s,
ultrapassa o automóvel.
1
A que distância após o sinal, o carro ultrapassará o
caminhão?
2
Qual a velocidade do carro nesse instante?
40/ 45
(Cinemática)
Física 1
40 / 45
Antoni
AA
Voa
Tea
vel
=
=
comida
A
E
m|s2
2.2
=
Ve
0
1-
Kc
Aa
£
a
=
9.5
=
-
Is
Vet
=
2
2
x
a
1.2
×
Kc
Va
=
ts
9.5
=
V.
,
Xo
=
2.2
+
=
×
aat
9.5£
8.64
82.0
=
=
t
⇒
2.2
×
=
8.64
s
-
8.64
s
19.0
m/s
41/ 45
(Cinemática)
Física 1
41 / 45
Exercícios
H 2.83 Um paraquedista salta e cai livremente por 50 m. Em
seguida o paraquedas se abre e ele desacelera a 2,0 m/s2 . Quando
chega ao solo, sua velocidade é de 3,0 m/s.
1
Quanto tempo o paraquedista fica no ar?
2
De que altura ele saltou?
42/ 45
(Cinemática)
Física 1
42 / 45
7
|
the
arias
-
Yo
.
Y
f
if
a
V.
=
=
A
Y
y
=
total
-
3i
.
14.2
50
=
gt
=
un
gts
£
t2
4.9
50
-
t
⇒
s
mls
31.4
-
3.2
=
:
{
+
.
4
ts
a
Is
m
4
V
=
mls
3
-
Zt
+
s
31.4
-
295
-
=
at
+
-
=
=
vot
-
.t
3n
-
V.
.
y
-
m1s2
2
-
3
-
2
tv
=O
-
vo
=
:
+
=
eho
=
Vo
Yo
:
V
I
Vo
50
-
The
cho
0
=
×
14.2
+
{
(
14.22
2
.
m
14
.
2
+
3.2
=
17.4
s
43/ 45
(Cinemática)
Física 1
43 / 45
H 2.68 Um modelo de foguete é lançado verticalmente e sobe
com uma aceleração constante de 4,00 m/s2 , por 6,00 s. Seu
combustível então acaba e ele passa a mover-se como uma
partícula em queda livre.
1
Qual a altura máxima atingida pelo foguete?
2
Qual o tempo total decorrido desde o lançamento até sua
queda na Terra?
44/ 45
(Cinemática)
Física 1
44 / 45
|
+
.hn/s2t=6.osV.=o
a
acaba
qdo
-
Vi
y
bmeremos
24
=
Y
Y
'
-
=
toot
yo
72
+
24T
}
.
-
ei
de
.
.
Is
.
4×63=72
n
snsiwdo
com
ele
snbina
tempo
were
ate
's
.co
-
of
.
power
0
0=24
⇒
24
.
esto
quarto
Vi
gt
-
=
ele
Is
-
vo
v=
+Iat2
saber
whocidade
sna
altima
mma
dai
pontin
4×6
=
a
trot
yo
=
a
Y
tat
V.
esta
e
combustive
o
-
9.8T
→
t=
2.451
zgt2
-
{
9.8×2.452
=
101.4
w
45/ 45
(Cinemática)
Física 1
45 / 45
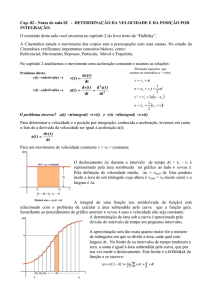
Obtenção de x t a partir de v t
Vimos como obter v t a partir de x t e a t a partir de v t .
Queremos agora fazer o processo inverso: Obter o espaço
percorrido x t2
x t1 a partir de v t .
Vamos começar usando o MRU: v constante ‹ v v v0
v
v0
x
t
x
x t2
x t1
v0 t
34/ 45
(Cinemática)
Física 1
34 / 45
Integral
Vamos considerar uma função v t qualquer. Dividimos o intervalo de tempo
em vários intervalos pequenos de larguras t1 t2 , de forma a poder
considerar v v .
x t2
x t1
vi ti
i
x t2
x t1
lim
t
0
vi ti
i
t2
t1
v t dt
35/ 45
(Cinemática)
Física 1
35 / 45
Obtenção de
x no MRUV
Para o MRUV, o gráfico de v t é uma reta. Podemos calcular a área sob a
curva entre os instantes t1 e t2 para saber o espaço percorrido x nesse
intervalo.
x
escolhendo t1
0 e t2
v1 t
1
a
2
t
2
t esta equação se torna x
x0
v0 t
1
2
2 at
36/ 45
(Cinemática)
Física 1
36 / 45
45/ 45
(Cinemática)
Física 1
45 / 45