Física - Etapa

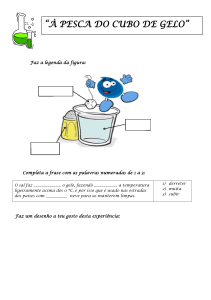
alternativa A
Questão 46
Um automóvel desloca-se a partir do repouso
num trecho retilíneo de uma estrada. A aceleração do veículo é constante e algumas posições por ele assumidas, bem como os respectivos instantes, estão ilustrados na figura abaixo. O gráfico que melhor representa a velocidade escalar do automóvel em função do tempo é:
Como a aceleração é constante, temos um
MRUV. Assim, do primeiro trecho do movimento,
vem:
0
v 0 + v1
∆S1
v
1,0
=
⇒ 1 =
⇒
2
∆t1
2
1,0
⇒ v1 = 2,0 m/s
O único gráfico onde a velocidade no instante
t1 = 1,0 s é v1 = 2,0 m/s é o da alternativa A.
Questão 47
a)
b)
Joãozinho abandona do alto de uma torre,
um corpo a partir do repouso. Durante a queda livre, com g constante, ele observa que nos
dois primeiros segundos o corpo percorre a
distância D. A distância percorrida pelo corpo
nos 4 s seguintes será:
a) 4D
b) 5D
c) 6D
d) 8D
e) 9D
alternativa D
Nos dois primeiros segundos o corpo percorre uma
distância D = g ⋅ 2 2 / 2 = 2 g . Nos seis primeiros
segundos o corpo percorre H = g ⋅ 6 2 / 2 = 18 g .
Assim, a distância percorrida (h) pedida é dada
por:
c)
d)
h = H − D = 18 g − 2 g = 16 g ⇒ h = 8D
Questão 48
e)
Um corpo de 200 g é lançado do solo, verticalmente para cima, com energia cinética
de 30 J. A aceleração gravitacional no local
vale 10 m/s2 e, durante a subida, 20% da
energia mecânica é perdida. A altura máxima
atingida por esse corpo é de:
a) 6 m b) 8 m c) 10 m d) 12 m e) 15 m
alternativa D
Sendo A o ponto de lançamento no solo e B o
ponto onde o corpo atinge altura máxima, do
enunciado, vem:
física 2
B
A
E mec.
= 0,8 E mec.
Adotando E g = 0 no ponto A, a equação anterior
fornece:
E gB = 0,8 E cA ⇒ mghmáx. = 0,8 E cA ⇒
⇒ 0,2 ⋅ 10 ⋅ hmáx. = 0,8 ⋅ 30 ⇒
⇒ hmáx. = 12 m
Questão 49
No conjunto abaixo temos uma barra homogênea, rígida, suspensa pela vertical que passa em seu centro de gravidade. Os corpos C1 e
C2 estão suspensos, respectivamente, nas extremidades A e B da barra. Para mantermos
essa barra em equilíbrio na direção horizontal, dentre outras possibilidades, devemos
suspender, no ponto:
Fazendo a soma dos momentos em relação ao
centro da barra (ponto P), no equilíbrio, temos:
L
ΣM P = 0 ⇒ 4g ⋅ L − 2g ⋅ L − mg ⋅
= 0⇒
2
⇒ m = 4 kg
Assim, para mantermos a barra em equilíbrio, podemos suspender no ponto C um corpo de 4 kg.
Questão 50
a) C, um corpo de 2 kg.
b) C, um corpo de 4 kg.
c) C, um corpo de 8 kg.
d) D, um corpo de 2 kg.
e) D, um corpo de 4 kg.
alternativa B
Para mantermos a barra em equilíbrio, sendo g o
módulo da aceleração da gravidade, uma possibilidade é esquematizada na figura:
Um bloco de massa 0,1 kg repousa sobre uma
superfície plana e horizontal. Em seguida, inclina-se a superfície lentamente até que o
mesmo comece a deslizar. Veja a ilustração a
seguir. A intensidade da força de atrito estático à qual esse bloco esteve sujeito, desde o
instante imediatamente anterior ao do início
da inclinação, até o instante imediatamente
anterior ao do início do deslizamento:
física 3
Dados: sen α = tan α = 0,1
g = 10 m/s2
a) foi constante e igual a 1 N.
b) foi constante e igual a 1 ⋅ 102 N.
c) variou de zero até 0,1 N.
d) variou de zero até 1 N.
e) variou de zero até 1 ⋅ 102 N.
temos visto nenhuma informação de temperaturas em Kelvin. Se o boletim meteorológico informa que no dia as temperaturas mínima e máxima numa determinada cidade serão, respectivamente, 23 oF e 41 oF, a variação dessa temperatura na escala Kelvin é:
a) −7,8 K
b) 10 K
c) 32,4 K
d) 283 K
e) 291 K
alternativa C
alternativa B
Marcando as forças no bloco nas duas situações,
vem:
A variação na escala Fahrenheit é ∆θf =
= 41oF − 23 oF = 18 oF . Da relação entre as variações de temperatura, temos:
∆θf
18
∆T
∆T
=
⇒
=
⇒ ∆T = 10 K
5
9
5
9
Questão 52
Num tubo em U de pequeno diâmetro e aberto em suas extremidades, temos uma quantidade de
água pura (ρA = 1,0 g/cm3 ) em
Para o bloco em repouso, na horizontal, temos
fat. = 0 .
Para o bloco na iminência de deslizamento, temos:
’
f at
. = P ⋅ senα = mg ⋅ senα = 0,1 ⋅ 10 ⋅ 0,1 ⇒
’
⇒ f at
. = 0,1 N
Assim, a intensidade da força de atrito variou de
zero até 0,1 N.
Questão 51
Temos visto ultimamente uma farta divulgação de boletins meteorológicos nos diversos
meios de comunicação e as temperaturas são
geralmente indicadas nas escalas Fahrenheit
e (ou) Celsius. Entretanto, embora seja a unidade de medida de temperatura do SI, não
repouso, como mostra a figura
ao lado. Por uma das aberturas
do tubo introduzem-se 2,0 cm3 de
um líquido não miscível, de densidade absoluta ρL = 0,8 g/cm3 e
espera-se seu estado de repouso. A melhor representação gráfica da situação final da experiência, com VA identificando o volume de água acima da linha horizontal que passa pelo ponto P, é:
a)
b)
física 4
c)
d)
⇒ 1,0 ⋅ VA = 0,8 ⋅ 2,0 ⇒
VA = 1,6 cm 3
Questão 53
Num copo de capacidade térmica desprezível
tem-se inicialmente 170 cm3 de água a 20 o C.
Para resfriar a água colocam-se algumas “pedras” de gelo, de massa total 100 g, com temperatura de −20 o C. Desprezando as perdas
de calor com o ambiente e sabendo que após
um intervalo de tempo há o equilíbrio térmico entre a água líquida e o gelo, a massa de
gelo remanescente no copo é:
e)
Dados:
ρágua
(densidade da água) = 1,0 g/cm3
cágua (calor específico da água) = 1,0 cal/(g.o C)
Lf (gelo) (calor latente de fusão do gelo) =
= 80 cal/g
c gelo (calor específico do gelo) = 0,5 cal/(g.o C)
a) zero
alternativa A
Na situação final, o estado de repouso pode ser
representado pela figura a seguir:
b) 15 g
c) 30 g
d) 38 g
e) 70 g
alternativa E
Sendo m a massa de gelo remanescente, Q A o
calor cedido pela água e QG o calor recebido pelo
gelo (calor latente + calor sensível), da conservação da energia, temos:
QG + Q A = 0 ⇒
⇒ ( mG − m ) ⋅ Lf + mG ⋅ cG ⋅ ( θ − θG ) +
+ mA ⋅ c A ⋅ ( θ − θ A ) = 0 ⇒
⇒ (100 − m) ⋅ 80 + 100 ⋅ 0,5 ⋅ (0 − ( −20)) +
+ 170 ⋅ 1,0 ⋅ (0 − 20) = 0 ⇒ m = 70 g
Questão 54
Pela Lei de Stevin temos:
pP = patm + ρ AghA
pQ = patm + ρLghL ⇒
pP = pQ
⇒ patm + ρ AghA = patm + ρLghL ⇒
⇒ ρ A ⋅ hA = ρL ⋅ hL ⇒ ρ A ⋅
VA
V
= ρL ⋅ L ⇒
A
A
Um pesquisador transferiu uma massa de
gás perfeito à temperatura de 27o C para outro recipiente de volume 20% maior. Para
que a pressão do gás nesse novo recipiente
seja igual à inicial, o pesquisador teve de
aquecer o gás de:
b) 30oC
c) 40oC
a) 20oC
d) 50oC
e) 60oC
física 5
alternativa E
Sendo a transformação isobárica e V2 = 1,2V1 , da
Lei de Charles, temos:
V1
V
V1
1,2 ⋅ V1
= 2 ⇒
=
⇒
T1
T2
(27 + 273)
T2
⇒ T2 = 360 K = 87 o C
Portanto, o pesquisador teve de aquecer o gás de
60 oC .
Questão 55
Sobre uma reta perpendicular a um espelho
plano existem os pontos A e B, situados a
40 cm e 140 cm, à sua frente, conforme ilustra a figura a seguir. Um objeto real é deslocado com velocidade constante de A para B,
sobre esta reta, num intervalo de 2,0 s. Nesse
tempo, a respectiva imagem conjugada:
Obedecendo às condições de simetria para o espelho plano, a imagem afasta-se do objeto com
velocidade v i = 2 ⋅ v o ⇒ v i = 1,0 m/s .
Questão 56
Uma pequena esfera
presa a um fio ideal,
fixo em uma das extremidades, constitui o
pêndulo simples ilustrado na figura ao lado.
Abandonando-se a esfera em A, ela demora
1,6 s para chegar até B.
Se a esfera for abandonada em C, o tempo necessário para chegar ao
ponto D é:
a) 0,20 s
b) 0,40 s
c) 0,80 s
d) 1,6 s
e) 3,2 s
alternativa D
O período independe da amplitude do movimento.
Assim, o tempo necessário para a esfera abandonada em C chegar em D é de 1,6 s.
Questão 57
a) permanece sempre num mesmo ponto.
b) aproxima-se do objeto com velocidade
1,0 m/s.
c) aproxima-se do objeto com velocidade
0,5 m/s.
d) afasta-se do objeto com velocidade
1,0 m/s.
e) afasta-se do objeto com velocidade
0,5 m/s.
de
de
de
Nos pontos A, B e C da figura fixamos corpúsculos eletrizados com carga elétrica idêntica. O corpúsculo colocado em A exerce sobre o colocado em B uma força de intensidade F. A força resultante que age sobre o corpúsculo colocado em B tem intensidade:
de
alternativa D
Para o deslocamento do objeto, temos:
∆So
1
vo =
⇒ vo =
⇒ v o = 0,5 m/s
∆t
2,0
a)
4F
9
b)
4F
5
c)
5F
9
d)
9F
4
e)
9F
5
física 6
alternativa C
As forças sobre B são mostradas a seguir:
Do cálculo da potência dissipada no resistor de
40 Ω, temos:
Pd = R ⋅ i 2 ⇒ 10 = 40 ⋅ i 2 ⇒ i = 0,5 A
5 ⋅ i = 2,5 A .
Assim, a corrente pedida é
Da Lei de Coulomb, vem:
F =
F’ =
k |Q A | ⋅ |QB |
r
2
k |QC | ⋅ | QB |
2
r’
R = F − F’
F =
⇒ F’ =
kQ 2
2
2
kQ 2
2
=
kQ 2
4
Questão 59
=
kQ 2
⇒
9
Quando a intensidade de corrente elétrica
que passa no gerador do circuito elétrico a seguir é 2,0 A, o rendimento do mesmo é de
80%. A resistência interna desse gerador
vale:
3
R = F − F’
F
⇒R =
5F
kQ 2
kQ 2
5 kQ 2
−
=
⋅
⇒ R=
9
4
9
9
4
Questão 58
No trecho de circuito representado a seguir,
a potência dissipada pelo resistor de 40 Ω é
10 W. A intensidade de corrente elétrica que
passa pelo resistor de 2 Ω é:
a) 1,0 Ω
d) 2,5 Ω
c) 2,0 Ω
b) 1,5 Ω
e) 3,0 Ω
alternativa E
Sendo 80% o rendimento do gerador, temos:
U
η=
= 0,8 ⇒ U = 0,8 ε
ε
Da equação do gerador, vem:
ε − ri
⇒ 0,2 ε =
U =
⇒ 0,8 ε =
2r ⇒
ε
ε−r
⋅2⇒
= 10r
Aplicando a Lei de Ohm-Pouillet no sentido horário, obtemos:
a) 2,5 A b) 2,0 A c) 1,5 A d) 1,0 A e) 0,5 A
alternativa A
Como a corrente em uma associação em paralelo
é inversamente proporcional à resistência, sendo
(i) a corrente no resistor de 40 Ω, temos:
ri −
ε + 12i
= 0 ⇒ 2r − 10r + 12 ⋅ 2 = 0 ⇒
⇒ 8r = 24 ⇒ r = 3 Ω
Questão 60
No circuito a seguir temos um gerador elétrico de força eletromotriz 6,0 V e resistência
interna de 0,050 Ω. Quando o amperímetro
ideal assinala 0 A, o voltímetro ideal assinala
_____ V, a carga elétrica do capacitor C1 é
_____ µC e a carga elétrica do capacitor C2 é
_____ µC.
física 7
alternativa A
Quando o amperímetro assinala 0 A, os capacitores
estão carregados e não há corrente elétrica no
circuito. Assim, o voltímetro indica a força eletromotriz do gerador, ou seja, assinala
LV = 6,0 V
.
Para os capacitores, temos:
C ⋅ C2
6,0 ⋅ 4,0
Ceq. = 1
=
= 2,4 µF
C1 + C 2
6,0 + 4,0
Assim, a carga em cada um dos capacitores é
dada por:
Os valores que preenchem correta e respectivamente as lacunas, na ordem de leitura, são:
a) 6,0; 14,4 e 14,4.
b) 5,95; 14,4 e 14,4.
c) 5,95; 9,6 e 14,4.
d) 6,0; 9,6 e 14,4.
e) 6,0; 14,4 e 9,6.
Q = Ceq . ⋅ U = 2,4 ⋅ 6 ⇒
Q = 14,4 µC