CAP 2 Medidas descritivas e gráficos básicos

Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
Capítulo 2. Medidas descritivas e gráficos básicos
Sumário
2.1 Introdução
2.2 Média
2.3 Mediana
2.4 Quartil
2.5 Medida de variabilidade – desvio padrão
2.6 O desvio padrão de Shewhart em Controle estatístico de qualidade
2.7 Desvio quartílico
2.8 Gráficos – Caixa das Medianas e Histograma
2.9 Questões para discussão e exercícios
2.10 Referências
Capítulo 2. Medidas descritivas e gráficos básicos
1
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
Capítulo 2. Medidas descritivas e gráficos básicos
2.1 Introdução
Quando o Gerente de produção mede e analisa uma característica da linha de produção,
uma característica física do produto ou uma medida do desempenho do processo, ele tem
em mente a melhoria do processo. Ele vê um sistema em movimento, uma combinação dos
insumos do processo, a atuação dos operadores juntos com a combinação dos insumos e as
atividades das máquinas, e finalmente o produto final. A visão do gerente é de aspectos
concretos da sua linha de produção e em termos sistêmicos.
O Estatístico por outro lado vai ver esse mesmo processo como algo mais abstrato, como
uma função de gerador de números. Ele vai ver se os números gerados são centrados e
simétricos ao redor de uma tendência central, se existir ou não alguns dados muito
discrepantes dos outros, se tiver ou não relações entre variáveis e dados diferentes.
É fácil ver que o gerente trabalhando sem a ajuda do Estatístico não vai captar todas as
informações disponíveis nos dados, e o Estatístico sozinho não vai saber onde ele deve
concentrar seus esforços para melhorar o processo. Portanto, o Gerente e o Estatístico têm
muito para ganhar trabalhando juntos.
Neste capítulo, noções preliminares sobre algumas medidas importantes que ajudam a
definir uma população de dados são introduzidas junto com alguns gráficos para enxergar
melhor a tendência central dos dados e outras características como a dispersão. No capítulo
anterior, argumentamos que certo nível de variabilidade é inerente a qualquer processo
industrial ou administrativo. Existem uma variabilidade aceitável e outra que extrapola os
limites de qualidade. Em CEQ, tentamos quantificar e identificar esses limites, e é assim
que o estudo de aleatoriedade fica tão importante.
Toda a área de estatística se baseia na pedra fundamental do conceito de variável aleatória.
É uma função que depende da média, da dispersão, da assimetria, e várias outras
características as quais, todas juntas, geram realizações de dados observados. O problema
todo é que nos não vemos a função gerando os dados, vemos apenas os dados. É dos dados
observados que podemos imaginar a forma da função. São as características das variáveis
aleatórias que são a preocupação principal do engenheiro ou administrador de processo.
Estabilizando as características da função da variável aleatória significa médias no alvo,
dispersão mínima, e previsibilidade assegurada. Conseqüentemente, os dados observados
subseqüentemente ficam dentro das especificações, e altos níveis de qualidade são
alcançados. Eventualmente dados observados díspares ocorrem em momentos raros, mas a
estabilidade do processo garante que são facilmente identificados, as causas eliminadas e
processos corrigidos.
2.2 Média
Em qualquer área de investigação onde números aparecem com freqüência, os profissionais
da área estudam maneiras e metodologias gráficas e estatísticas para expressar esses
números mais claramente e mais resumidamente. Isso é um dos objetivos principais do
Capítulo 2. Medidas descritivas e gráficos básicos
2
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
trabalho dos gerentes e estatísticos. Por exemplo, existem várias maneiras de medir a
tendência central dos dados, e nenhuma maneira é necessariamente o melhor, tudo depende
da situação. O cálculo de uma tendência central é importante porque ela consegue
condensar uma série de dados em um único número. Certamente a mais popular é a média
n
X , chamado mesmo de x-barra, a soma de uma série de dados
X
i 1
i
dividida pelo
número n de dados na soma. Em termos matemáticos, então, podemos escrever
n
X
X
i 1
n
i
.
Na tabela 2.1, são colocadas 50 medidas em milímetros do comprimento de uma peça, por
sinal, uma das características essenciais da peça. Uma coluna de números não é nada
interessante para o engenheiro, como a primeira coluna da tabela. Por outro lado, a média
das medidas da primeira coluna da tabela é
100,324 = (102,230 + 99,070 + 99,079 + ... + 98,143)/50,
e o engenheiro agora pode saber se o produto está sendo fabricado centrado no alvo
desejado.
Um problema que pode ocorrer é que a média perde a sua representatividade quando, entre
os números, existem valores muito diferentes dos outros. Esses valores levam a média para
um valor muito longe da tendência central dos dados, e não muito perto dos outros
números. Uma maneira de resolver o problema dessa distorção seria simplesmente eliminar
esses números, no entanto o gerente não recomenda esse caminho por causa de certo grau
de arbitrariedade. Podemos eliminar dados que são realmente errados, por erros de
digitação, ou medição, por sinal. Por exemplo, o gerente pode sentir uma necessidade de
eliminar o valor 102,557 da tabela 2.1 como o maior (e pior) dos números, mas para qual
razão? Não é justificativo tirar um número da amostra porque o chefe não vai gostar vê-lo.
Se não tiver nenhuma boa justificativa para tirá-lo, por exemplo, poderia ter sido o
resultado de uma mensuração mal feita e errada, o número fica. Na próxima seção é
apresentada uma medida de tendência central para dados assimétricos e na presença de
dados suspeitos.
Capítulo 2. Medidas descritivas e gráficos básicos
3
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
Dados
Dados
Comentário Contador
originais ordenados
Ordem
102,230
99,070
99,079
97,818
101,901
102,000
101,797
100,894
98,572
101,259
102,168
99,005
102,557
102,230
102,223
102,170
102,168
102,101
102,090
102,000
101,995
101,990
101,901
101,900
Máximo
1
2
3
4
5
6
7
8
9
10
11
12
Quartil
13
99,073
101,810
101,775
97,962
101,480
101,995
98,477
102,090
98,476
101,780
102,170
100,827
101,990
101,797
101,780
101,775
101,773
101,607
101,480
101,408
101,276
101,259
101,178
100,988
99,182
98,254
100,894
100,827
101,810
98,140
102,557
100,636
100,428
100,410
100,355
101,276
100,355
99,182
102,223
101,773
98,677
101,178
100,428
98,940
99,079
99,073
99,070
99,005
98,940
98,677
101,408
98,572
101,900
98,253
102,101
100,988
98,310
101,607
97,876
100,636
97,968
97,929
100,410
98,477
98,476
98,310
98,254
98,253
98,143
98,140
97,968
97,962
97,929
97,876
98,143
97,818
14
15
16
17
18
19
20
21
22
23
24
Mediana =
100,861
25
26
27
28
29
Média =
100,324
30
31
32
33
34
35
36
37
Quartil
38
39
40
41
42
43
44
45
46
47
48
49
Mínimo
50
Tabela 2.1 – Comprimento de barra de ouro em mm, n = 50.
Capítulo 2. Medidas descritivas e gráficos básicos
4
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
2.3 Mediana
Para resolver a distorção de números discrepantes e assimétricos, utiliza-se da mediana, o
número no meio dos números ordenados (ou a média dos dois números no meio dos
números), nesse caso, na tabela 2.1,
100,861 ( = (100,827 + 100,894)/2).
Vamos explicar melhor. Numa relação de números ordenados do maior para o menor existe
um número que separa todos os números em dois grupos de tamanho igual, os números
maiores que a mediana e os números menores. Na lista dos 50 números, há 25 números
maiores que 100,861 e 25 números menores. Pode notar que quando o número de dados é
ímpar a mediana é exatamente o número no meio dos números ordenados, sem a
necessidade de calcular a média dos dois números no meio. Os analistas argumentam que a
mediana é melhor do que a média para representar a tendência central dos números na
presença de dados muito diferentes que os outros. Isso ocorre porque a mediana é
insensível aos valores muito grandes ou muito pequenos. Se for alterado o valor de 102,557
para 1.025.566,0 o valor da mediana não mudaria, porque com a mediana de 100,861, ainda
tem a metade dos dados por cima e a metade dos dados por baixo da mediana. A diferença
numérica entre a mediana e a média no exemplo da tabela 2.1
(100,861 - 100,324 = 0,537)
poderia ser considerada razoavelmente grande pelo engenheiro, se for considerada pequena
a variabilidade dos números, e significaria que a média é realmente distorcida como medida
de tendência central, levando o engenheiro a utilizar a mediana.
Aqui temos uma lição importante da área de estatística, distancias e tamanhos e outras
mensurações devem ser analisadas em termos da variabilidade dos dados, e não em termos
das unidades originais como milímetros ou gramas. Esse conceito é essencial para as
ferramentas de gráficos de controle nos capítulos seguintes.
2.4 Quartil
Os quartís são calculados, partindo da mediana. Com a mediana os dados ordenados foram
divididos em dois subgrupos, acima e abaixo da mediana. Para cada subgrupo encontra-se
sua própria mediana e essa mediana se chama de quartil. Obviamente tem um quartil
inferior, o primeiro quartil, e um quartil superior, o terceiro quartil. Para completar o
raciocínio, pode chamar a mediana de segundo quartil. Os quartis dividem os dados
ordenados em quatro grupos distintos, cada grupo tem um quarto dos dados. No exemplo
na tabela 2.1, cada um dos quatro subgrupos tem aproximadamente 50/4 elementos. Os
quartís são assinalados na tabela 2.1: quartil inferior de 98,572 e quartil superior de
101,810. A diferença numérica entre os quartís superior e inferior, o desvio quartílico, pode
ser utilizada também para definir a variabilidade dos dados, assunto detalhado na seção 2.7.
2.5 Medida de variabilidade – desvio padrão
Capítulo 2. Medidas descritivas e gráficos básicos
5
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
Igualmente importante com as medidas de tendência central são as medidas de dispersão,
representando como os dados se espalham ao redor da média. Quando os números são
sempre próximos à média, isso significa que a tendência central representa bem os dados.
No entanto, se números ficam longe da média, então a média não representa muito bem
todos os dados. A idéia de variabilidade é importante na área de engenharia de qualidade,
como foi destacado na introdução desse livro, porque oferece uma definição operacional
para qualidade, uma definição que permite medições e análise concretas, e discussões
objetivas. Peças fabricadas que exibem mensurações muito espalhadas não têm qualidade,
pois muitas peças vão acabar rejeitadas e retrabalhadas, significando custos altos de
fabricação e posição fraca em termos da competição empresarial do mercado.
O desvio ao redor da média é definido como a diferença entre um número individual e a
média de todos os dados. Por exemplo, a tabela 2.2 mostra 30 dados de tempo gasto pela
empresa para solucionar problemas dos clientes do momento do recebimento da queixa até
que a solução seja conferida. A média de tempo gasto é 182,89 minutos, um pouco mais
que 3 horas. O primeiro desvio calculado (na terceira coluna) é
-82,89 = 100 – 182,89 = desvio = X i  X .
É uma tradição dos estatísticos de colocar na expressão do desvio a média depois do dado
individual. Assim, quando a média é menor que o dado individual o desvio é positivo e
vice-versa. É muito interessante calcular a média dos desvios que representaria a
variabilidade dos dados. Como fica demonstrada na tabela 2.2, a soma dos desvios é
sempre igual a zero, é uma fatalidade matemática, e, portanto a média dos desvios também
é sempre igual a zero. Então a questão é como calcular a média dos desvios numa maneira
consistente e esclarecedora. A quarta coluna da tabela 2.2 contém os mesmos desvios da
terceira coluna, mas essa vez sem o sinal do desvio, chamada o módulo ou valor absoluto
do desvio. A média dos desvios nessa coluna e 75,83. Intuitivamente isso é a melhor
maneira, sem dúvida, de calcular a variabilidade dos dados, no entanto, na estatística existe
outra maneira mais confusa.
Por razões históricas e por causa de algumas características matemáticas difíceis de
compreender, mas muito importante para o teórico, a média do desvio sem sinal não e
tipicamente utilizado em estudos estatísticos e nem no chão da fábrica. Para resolver o
2
problema do sinal do desvio, é preferível utilizar o quadrado do desvio X i  X  , também
sem sinal, todos somados como antes e a média deles calculada1:
( X i  X )2
= Variância = 
= SQT/(n – 1)
n 1
i 1
n
SX2
A expressão SQT é usada na área de regressão, assunto do capítulo 13. A média dos
quadrados dos desvios leva o nome técnico de variância. Para chegar a uma medida do
desvio médio então é necessário aplicar a raiz quadrada à variância. Esse desvio
O símbolo X é utilizado para representar a média de uma amostra e pode ser calculado, e μ X a média da
população, e geralmente não é calculável porque a população é grande demais ou a mensuração implica em
destruição do objeto mensurado, etc.
1
Capítulo 2. Medidas descritivas e gráficos básicos
6
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
Código da
reclamação
123
872
478
123
301
261
222
182
143
104
164
158
169
179
190
200
211
222
232
243
253
264
275
285
296
306
317
328
338
349
Tempo gasto em
minutos
100,00
216,01
113,42
287,33
221,47
194,95
161,55
325,89
292,62
266,38
106,19
307,56
255,49
203,39
148,71
17,00
66,78
165,34
95,20
102,95
427,43
186,34
82,04
59,00
36,00
168,89
207,95
217,94
225,79
227,19
Desvio ao redor
da média
-82,89
33,11
-69,47
104,43
38,58
12,06
-21,35
142,99
109,73
83,49
-76,70
124,66
72,59
20,50
-34,19
-165,89
-116,11
-17,55
-87,70
-79,94
244,53
3,45
-100,85
-123,89
-146,89
-14,00
25,05
35,05
42,90
44,30
Módulo do desvio (valor
absoluto)
82,89
33,11
69,47
104,43
38,58
12,06
21,35
142,99
109,73
83,49
76,70
124,66
72,59
20,50
34,19
165,89
116,11
17,55
87,70
79,94
244,53
3,45
100,85
123,89
146,89
14,00
25,05
35,05
42,90
44,30
Desvio
quadrado
6871,36
1096,46
4826,37
10906,22
1488,33
145,42
455,70
20447,30
12040,82
6970,70
5882,76
15541,31
5269,52
420,24
1168,83
27520,70
13481,55
308,07
7690,68
6390,97
59796,28
11,91
10171,11
15349,64
21577,74
195,97
627,58
1228,18
1840,23
1962,51
Soma da coluna
5486,8
0,00
2274,84
261684,46
Media =
182,89
0,00
75,83
8722,82
Amplitude Total
410,43
Raiz da média do desvio
quadrado =
93,40
Desvio padrão =
94,99
Tabela 2.2 - Minutos corridos até solucionar a reclamação do cliente, e desvios.
médio tem outro nome em estatística, o desvio padrão (SX = √SX2). Para os dados da tabela
2.2, o desvio padrão é 94,99. Nota-se que para formar o desvio padrão a soma dos
quadrados não é dividida pelo número de dados na coluna (n = 30), mas sim por um
Capítulo 2. Medidas descritivas e gráficos básicos
7
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
número chamado de grau de liberdade, aqui igual a (n -1 = 29), um conceito discutido mais
tarde. Muitas vezes é enfatizado que este desvio padrão se baseia em valores individuais,
um conceito retomado na apresentação do desvio padrão de Shewhart.
Um conceito muito importante para os gráficos de controle estudados na segunda parte do
livro é o desvio padrão de uma coleção de médias, e leva o nome erro padrão. É quase igual
ao desvio padrão, mas a diferença é que é dividido pela raiz quadrada do tamanho da
amostra n .
S
erro padrão = S X  X
n
O desvio padrão das médias é pelo menos igual ao desvio padrão dos dados individuais,
quer dizer, quando o tamanho n da amostra é maior que um, o desvio padrão das médias é
menor. No final, é para esperar menor variação nas médias que efetivamente eliminam
valores muito altos acima da média com os valores muito abaixo da média. Por exemplo, o
desvio padrão do peso de uma turma de alunos pode ser 30 quilogramas, mas se for
analisado o conjunto de médias de várias turmas o desvio padrão das médias seria bem
menor refletindo o fato que médias variam menos que os valores individuais. E mais, a
variação das médias diminui quando o tamanho da amostra aumentar. Esta relação é
ilustrada na figura 2.1 para o caso da distribuição normal, assunto prioritário do próximo
capítulo. Veja como a distribuição fica cada vez mais apertada nos valores centrais, e
caudas mais finas, demonstrando precisão maior. Portanto, amostras maiores fornecem um
erro padrão menor e conseqüentemente mais segurança na representação da população,
diminuindo o risco de obter estimativas de estatísticas como a média longe dos parâmetros
da população.
Distribuição normal com tamanhos da amostra diferentes
n = 16
n=9
n=4
n=1
Figura 2.1 – A distribuição normal para médias para vários tamanhos amostrais
Capítulo 2. Medidas descritivas e gráficos básicos
8
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
No final, voltando para os dados de tabela 2.2, considerando o tamanho da média (182,89),
a diferença entre o desvio absoluto médio (75,83) e o desvio padrão (94,99) é relativamente
grande. Isso sugere que a escolha entre as duas medidas levanta uma dúvida para medir a
variabilidade dos dados, mas como já foi colocado acima, o desvio padrão é preferível, se
não pela lógica então sim pela tradição. Consistência é a palavra chave, os dois conceitos
não devem ser misturados no mesmo procedimento. Uma vez utilizado um conceito p0ara
medir variabilidade, não deve ser trocado por outro.
2.6 O desvio padrão de Shewhart em controle estatístico de qualidade
Na área de controle estatístico de qualidade há mais uma maneira de calcular o desvio
padrão, através de uma fórmula desenvolvida pelo próprio Shewhart para facilitar o
cálculo no chão da fábrica. Lembre-se que ele estava trabalhando nesses procedimentos na
década de 1930 sem informática e automação, e precisava de procedimentos fáceis, mas
cuidadosos, para monitorar a qualidade da fabricação. Como será visto na segunda parte
do livro sobre ferramentas de controle e monitoramento do processo, a utilização de
amostras muito pequenas é a regra para um grande conjunto de gráficos de controle. Por
exemplo, o operador pode monitorar o processo com bastante segurança praticando
mensurações de apenas 5 peças por hora (tamanho da amostra n = 5) de lotes muito
maiores de centenas ou milhares de peças. Para simplificar o calculo do desvio padrão, o
operador calcula a amplitude (valor máximo menos o valor mínimo) de cada amostra e
disso calcula a média das amplitudes ( R ). Shewhart desenvolveu uma tabela de
coeficientes d2, mostrados na tabela 2.3, com o poder de transformar R em desvio padrão,
R
. Nota-se que o valor de d2 aumenta com o tamanho da amostra.
d2
Tamanho da amostra = n
n=
d2
B3
B4
D3 (R) D4 (R)
A2 ( X )
2
1,128
0
3,267
0
3,267
1,880
3
1,693
0
2,568
0
2,575
1,023
4
2,059
0
2,266
0
2,282
0,729
5
2,326
0
2,089
0
2,115
0,577
6
2,534 0,03
1,97
0
2,004
0,483
7
2,704 0,118 1,882 0,076
1,924
0,419
8
2,847 0,185 1,815 0,136
1,864
0,373
9
2,970 0,239 1,761 0,184
1,816
0,337
10 3,078 0,284 1,716 0,223
1,777
0,308
11 3,173 0,321 1,679 0,256
1,744
0,285
12 3,258 0,354 1,646 0,284
1,716
0,266
13 3,336 0,382 1,618 0,308
1,692
0,249
14 3,407 0,406 1,594 0,329
1,671
0,235
15 3,472 0,428 1,572 0,348
1,652
0,223
20 3,735 0,51
1,49
0,414
1,586
0,180
25 3,931 0,565 1,435 0,459
1,541
0,153
Capítulo 2. Medidas descritivas e gráficos básicos
9
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
Tabela 2.3 - Coeficientes de Shewhart para os gráficos de controle
Os outros coeficientes nas outras colunas da tabela 2.3 são também muito importantes e
serão utilizados na segunda parte do livro na construção de gráficos de controle.
Para ilustrar o cálculo do desvio padrão de Shewhart, os dados da tabela 2.2 foram
arranjados em seis subgrupos de tamanho 5. Veja tabela 2.4. Este tamanho de 5 é comum
nas fabricas para monitoramento de processos. Subgrupos amostrais são levantados em
períodos regulares, hora em hora, ou uma vez por turno, ou uma vez por dia, por exemplo.
Na tabela fica claro que cada subgrupo tem uma média e uma amplitude. A média das
amplitudes R é 187,308. Então uma estimativa do desvio padrão seria,
R
= 187,308/2,326 = 80,528.
d2
Temos que lembrar que os coeficientes e cálculos de Shewhart são aproximações
matemáticas desenvolvidas para facilitar a análise da variabilidade da produção
especialmente nos momentos críticos sofridos no chão da fábrica. As aproximações nunca
representam perfeitamente bem os conceitos mais corretos, mas quando tempo gasto numa
operação é essencial, a aproximação serve muito bem, nesse caso já comprovado por mais
que 70 anos de prática no mundo real.
Observação
Amostral
1
Subgrupo
1
2
3
4
5
6
168,890
161,550
307,560
66,780
186,340
207,950
2
207,950
325,890
255,490
165,340
82,040
217,940
3
217,940
292,620
203,390
95,200
59,000
225,790
4
5
225,790
266,380
148,710
102,950
36,000
227,190
227,190
106,190
17,000
427,430
168,890
182,890
Média
das
médias =
Média
subgrupo
209,552
230,526
186,430
171,540
106,454
212,352
Amplitude
subgrupo
58,300
219,700
290,560
360,650
150,340
44,300
182,89
Amplitude
média =
Desvio
padrão
Shewhart =
187,308
80,528
Tabela 2.4 - Minutos corridos até solucionar a reclamação do cliente, dados arranjados em
6 subgrupos amostrais com 5 observações em cada grupo.
O desvio padrão de Shewhart é menor que o desvio padrão calculado na base de valores
individuais, considerando que no de Shewhart é utilizada a variação dentro de subgrupo e
não entre subgrupos. Ou seja, o desvio padrão de Shewhart elimina a variação de medias
dos subgrupos e, portanto é menor que o desvio padrão de valores individuais que aceita
toda variação, dentro do subgrupo e entre subgrupos. Na tabela 2.4, nota-se a grande
Capítulo 2. Medidas descritivas e gráficos básicos
10
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
diferença entre medias de cada subgrupo, a média menor é 106,4 e a maior é 230,5. O
desvio padrão de Shewhart não inclui esta diferença entre subgrupos.
2.7 Desvio quartílico
Outra medida de variabilidade é o desvio quartílico, a diferença entre o quartil inferior e o
quartil superior já estudado anteriormente na seção sobre a mediana. Voltando para a tabela
2.1 sobre o comprimento em mm, pode ser visto que o desvio quartílico é igual a
3,238 = 101,810 – 98,572.
Como a mediana, o desvio quartílico tem a vantagem de não ser afetado por valores muito
discrepantes. No entanto, a sua utilização na estatística aplicada não é muito comum,
constando em alguns pacotes de software especializado, mas na prática desprezado a favor
do desvio padrão. No entanto, no famoso gráfico da caixa das medianas (box-plot, em
inglês) a sua presença é essencial. Veja a próxima seção.
Resumindo em termos do exemplo sobre as reclamações, o gerente da empresa possui pelo
menos duas medidas para analisar o desempenho da empresa frente aos clientes com
queixas: a média do tempo gasto para solucionar a reclamação e o desvio padrão desse
tempo. Um procedimento prático pode ser colocado nos manuais da empresa, onde
semanalmente médias e desvios padrões são calculados e tendências analisadas e
providências tomadas se forem necessárias. Por exemplo, a média das reclamações
tendendo a subir ou o desvio padrão aumentando através do tempo são sinais claros de
deterioração do desempenho, e deve causar preocupação na parte da gerência. Os dados
individuais devem sofrer também uma análise detalhada, especialmente dados que se
destacam longe dos outros.
2.8 Gráficos – Caixa das Medianas e Histograma
Sem dúvida, a melhor maneira de analisar uma série de dados é graficamente. A tentativa
de ver padrões e tendências em uma relação de dados escritos em uma tabela certamente
resultará em confusão especialmente quando o número de dados é grande. A figura 2.2
mostra os dados da tabela 2.2, o tempo gasto em resolver problemas dos clientes. Entre
vários outros pontos, pelo menos dois são destacados, o ponto máximo no dia 21 e o ponto
mínimo no dia 16. O que aconteceu nesses dois dias? Será que os eventos que ocorreram no
dia 16 são controláveis e que podem ser repetidas nos outros dias para tirar proveito da
situação? E os eventos do dia 21 que causaram um péssimo desempenho, será que eles
podem ser evitados no futuro?
Capítulo 2. Medidas descritivas e gráficos básicos
11
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
450,00
400,00
350,00
300,00
250,00
200,00
150,00
100,00
50,00
0,00
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
Dias do mes
Figura 2.2 - Tempo gasto em resolver problemas dos clientes
Um gráfico que reúne as informações da mediana e dos quartis em uma maneira fácil para
entender é a caixa das medianas, figura 2.3.
Figura 2. Caixa de medianas dos dados de tempo gasto na tabela 2
450,00
400,00
350,00
300,00
250,00
200,00
150,00
100,00
50,00
0,00
Figura 2.3 - Caixa de medianas para o tempo gasto nas reclamações na tabela 2.2
As duas linhas extremas horizontais representam os valores mínimos e máximos de toda a
série, ou em outras palavras, a distância entre elas é a amplitude geral dos dados. A caixa
no meio da figura representa o quartil inferior e o superior, ficando agrupadas a metade
Capítulo 2. Medidas descritivas e gráficos básicos
12
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
central dos dados, e a distância entre esses valores é o desvio quartílico. Finalmente, a linha
dentro da caixa é a mediana. Pode ver pela localização da caixa que os dados estão
distribuídos com assimetria, tendo mais valores relativamente baixos que altos. Os valores
altos são menos freqüentes, mas merecem uma investigação cuidadosa para apurar suas
causas especiais. Nesse caso, esses valores altos, que representam um péssimo desempenho
da empresa em solucionar problemas dos clientes, são críticos para o relacionamento da
empresa com o seu público, e a gerência deve garantir que insatisfações não acontecem no
futuro.
Muitas empresas montam essa figura para importantes características operacionais em uma
base mensal ou semanal facilitando o monitoramento da característica. É fácil ver se a
característica está no alvo ou evoluindo numa maneira satisfatória, e se a variabilidade dos
dados está aumentando (piorando) ou diminuindo (melhorando). Veja figura 2.3, onde se
apresenta uma série temporal de caixas de medianas mostrando o perfil de uma máquina em
períodos seqüenciais funcionando ou parada durante um intervalo de três meses. Veja todos
esses dados no anexo do capítulo 12. A primeira caixa mostra que a mediana dos tempos da
máquina em funcionamento é em torno de 15 horas. Quer dizer, quando a máquina está
trabalhando fica funcionando direto durante aproximadamente 15 horas. Este valor é menos
que o alvo da fábrica o qual é 16 horas (dois turnos de 8 horas). O quartil inferior em 8
horas e o quartil superior em 16 horas significam assimetria nos números com observações
muito abaixo da mediana de 15, e um desvio quartílico relativamente grande de 8 horas.
Nota-se que o segundo mês tinha o melhor desempenho. A mediana do tempo funcionando
é levemente mais alta e o desvio muito menor. Nesse mesmo mês, tempo parado tem o
menor desvio. Enfim, a empresa deve estudar os números do segundo mês para identificar
os fatores responsáveis para esta estabilidade tão marcante. Na realidade, foi iniciado no
segundo mês um programa de manutenção preventiva para a máquina em questão que
praticamente eliminou paradas inusitadas por causa de quebra de ferramentas.
Finalmente, na caixa de medianas, notam-se as estrelinhas (*) acima e abaixo de algumas
caixas. Esses dados são considerados como suspeitos, e merecem investigação concentrada.
Eles são estranhamente distantes das medianas, muito mais distantes que o esperado, nesse
caso mais que dois desvios quartílicos. Aberrações dessa natureza possuem muita
informação para melhorar os respectivos processos.
Capítulo 2. Medidas descritivas e gráficos básicos
13
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
Caixa de medianas - tempo funcionando e tempo parado - 3 meses
20
Horas
15
10
5
0
tempo func 1
tempo parado 1
tempo func 2
tempo parado 2
tempo func 3
tempo parado 3
Figura 2.3 - Caixa de medianas para o tempo de máquina funcionando e parado2
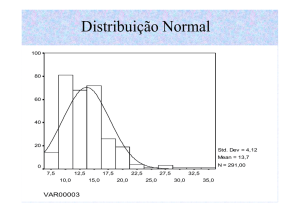
Finalmente apresenta-se o histograma, um gráfico que tem todas as boas características da
caixa de medianas, mas exibe muito mais informação sobre a distribuição dos dados. Foram
amostrados em um laticínio 150 sacos de leite contendo por lei 1 litro do alimento. O
histograma é um retrato dos dados na tabela 2.5, logo em seguida.
2
Figura 2.3 foi desenhada com o apoio do software Mini-tab, versão gratuita. www.minitab.com/downloads
Capítulo 2. Medidas descritivas e gráficos básicos
14
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
Histograma
F
r
e
q
u
e
n
ci
a
30
120,00%
25
100,00%
20
80,00%
15
60,00%
10
40,00%
5
20,00%
0
0,00%
856 878 900 922 945 967 989 1011 1033 1055 1078 1100 maior
Figura 2.4 - Histograma de medidas de sacos de leite de um litro.
Classes até
Freqüência
856,44
878,61
900,77
922,94
945,10
967,27
989,43
1011,60
1033,77
1055,93
1078,10
1100,26
maior
1
1
1
3
19
19
25
21
23
19
10
4
4
Cumulativa
%
0,67%
1,33%
2,00%
4,00%
16,67%
29,33%
46,00%
60,00%
75,33%
88,00%
94,67%
97,33%
100,00%
Tabela 2.5 - Freqüências de medidas em ml de sacos de leite de um litro. 3
Na primeira linha da tabela 2.5, entre os 150 sacos investigados um saco entra na classe de
pesos de zero a 856,44 ml. Na próxima linha, a classe de sacos entre 856,44 ml a 878,61 ml
tem de novo somente um saco. A freqüência mais popular onde caíram 25 sacos de leite é a
de 967,27 a 989,43. Cada classe possui o mesmo tamanho de aproximadamente 22 ml.
3
Ishikawa, Kaoru (1990) escreveu que existem 7 importantes ferramentas de qualidade: gráficos de controle
(neste livro capítulo 7), histograma, ficha de verificação, gráfico de causas (espinha de peixe), fluxograma,
diagrama de dispersão (terceira parte neste livro) , e gráfico de Pareto.
Capítulo 2. Medidas descritivas e gráficos básicos
15
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
Pode haver uma pequena diferença comparando tamanhos das classes em função de
pequenos erros de arredondamento. A última coluna da tabela 2.4 mostra a percentagem
cumulativa de freqüências até o limite máximo daquela classe. Por exemplo, de todos os
sacos amostrados, 16,67% tem volume até 945,10 ml, o limite mínimo permitido por lei
(950 ml). Em outras palavras quase 17% da produção do laticínio é exposta a multas. É
claro que isso significa que aproximadamente 83% dos sacos têm tamanho maior que o
limite mínimo.
Toda essa informação também consta na figura 2.4, o histograma, mas numa maneira mais
clara e mais fácil compreender, graficamente. Por sinal, a forma do histograma, com
freqüências altas no meio do gráfico e freqüências mais baixas (mais raras) para números
distantes da tendência central é muito comum. Essa constatação é a base da famosa
distribuição normal, e dizem os Estatísticos que sem a distribuição normal não existiria a
área de estudo chamado Estatística. O histograma apresenta um diagrama simples para ver
a tendência central dos dados e a variabilidade melhor que a caixa das medianas. Essa
ferramenta é utilizada para analisar dados através do tempo. Por exemplo, um engenheiro
trabalhando na linha de produção utilizaria o histograma periodicamente para verificar se a
característica está no alvo e a dispersão dos dados não está escapando de um controle
adequado. Os gráficos de controle na sua essência são construídos supondo que os dados
seguem a distribuição normal. Se ocorrer discrepâncias, quer dizer, se dados aparecem
longe da média nas caudas da distribuição, elas devem ser investigadas e o processo
corrigido.
Muitas vezes o analista não utiliza a freqüência absoluta no eixo vertical como foi mostrado
na figura 2.4, mas sim a freqüência em termos percentuais. Assim, cada coluna do
histograma representa uma percentagem da amostra, e, se a amostragem for bem-feita e
consequentemente for representativa, as classes e suas respectivas percentagens devem
refletir a mesma estrutura na população. É importante enfatizar que a soma das
percentagens de todas as classes é naturalmente 100%. Isso fica claro também na última
coluna da tabela 2.5.
Nos próximos dois capítulos, serão elaboradas as distinções entre varias distribuições de
probabilidade, matéria essencial para todos os capítulos subseqüentes, mas especialmente
para a utilização de gráficos de controle da segunda parte do livro.
2.9 Questões para discussão e exercícios
1. A qualidade de uma mercadoria depende essencialmente das suas características
quantitativas, como peso e comprimento, e não das características qualitativas e intuitivas.
No final, para uma operação ser rentável, o consumidor tem que gostar da mercadoria
oferecida e isso depende totalmente da objetividade e não da subjetividade da soma das
características.
2. Os coeficientes de Shewhart são apenas aproximações às formulas exatas, mas ainda
assim com PCs e laptops em todo lugar, até hoje são utilizados estes coeficientes em
fábricas no mundo inteiro. Teria alguma idéia por quê?
Capítulo 2. Medidas descritivas e gráficos básicos
16
Controle Estatístico de Qualidade (CEQ)
Robert Wayne Samohyl Ph.D.
3. Sabemos que ambos os gráficos, a caixa de medianas e o histograma, são excelentes
para monitorar a tendência central e a dispersão de mensurações de características
importantes do processo e produto. No entanto, o histograma possui mais informações do
que a caixa de medianas. Se for visitar uma fábrica, a probabilidade de ver a caixa de
medianas em utilização é bem maior do que o histograma. É um paradoxo ou existe
alguma razão para usar a ferramenta menos informativa?
4. No seu lugar de trabalho, faça mensurações de alguma característica importante do
processo onde você mesmo se insere. Se fosse linha de produção, poderia ser alguma
característica do produto, ou se estivesse em escritório administrativo, poderia ser alguma
medida de desempenho talvez em termos de horas e minutos para completar determinada
tarefa. Coloque os dados numa ficha de verificação, e tentar coletar pelo menos 8 amostras
por dia de tamanho 9, um total de 72 mensurações por dia e em 5 dias um total de 360
mensurações. Com esses dados, construir um histograma e uma caixa de medianas dia a
dia. Certamente vai ver ciclos e padrões na seqüência dos gráficos durante a semana.
Comentar sobre a variabilidade da média e a dispersão dos dados. Encontrou alguma causa
para explicar esses movimentos?
2.10 Referências
MONTEIRO, M., Coordenação. Gestão da Qualidade, Teoria e Casos, Editora
Elsevier/Campus, 2006.
Ishikawa, K. (tradução: John H. Loftus). Introduction to quality control 3ª. Ed. Tokyo:
3A Corporation, 1990.
Capítulo 2. Medidas descritivas e gráficos básicos
17