mruv sobre um plano inclinado

Física Experimental I
EXPERIMENTO 02:
1.
Prof. Robinson
MOVIMENTO RETILINEO UNIFORMEMENTE VARIADO
OBJETIVO
Este experimento tem como objetivo caracterizar o MRUA; estudar as equações e os
diferentes gráficos do MRUA e interpretá-los;
2.
INTRODUÇÃO
A característica fundamental do movimento retilíneo uniformemente variado (MRUV) é de
fato a aceleração ter um valor constante ao longo de todo o movimento. Desde ótica, vamos
descrever e estudar esse movimento através de um móvel se deslocando sobre a superfície de um
plano inclinado, figura 1. Por tanto, o primeiro passo é mostrar do movimento efetivamente do tipo
MRUV. Diante disto, utilizamos o diagrama de corpo isolado descrito na figura e aplicamos a
Segunda Lei de Newton:
=
=
= O módulo da componente da força aplicada, paralela ao plano, sobre o móvel é:
= ∙ = ∙ ∙ Onde P representa o peso do móvel. Portanto, a aceleração do móvel que se desloca em linha reta
sobre o plano inclinado é:
= ∙ (eq.1)
Observamos que a aceleração do móvel é constante desde que e o ângulo de inclinação do plano
continue fixo. Também devemos observar que esta equação é válida para casos de moveis que estão
se deslocando e não estão rodando. Para corpos que estão deslocando-se por rotação pura sobre o
plano, o movimento também é MRUV, porém a equação anterior não é válida para esse tipo de
movimento.
Figura 1. Representação esquemática de um móvel de massa m deslocandose sobre um plano inclinado com ângulo . São mostradas a força
gravitacional P e sua componente na direção paralela ao plano.
Física Experimental I
3.
Prof. Robinson
FUNDAMENTAÇÃO TEORICA
Neste experimento será utilizado um plano inclinado com baixo ângulo (~ 5º) para simular um
movimento retilíneo de um móvel com aceleração constante. Considerando o esquema da figura 2,
podemos observar de modo geral que a velocidade média , entre dois pontos (n e n+1) esta
dado pela equação:
∆
, = ∆ = (eq. 2)
De forma similar, a aceleração média , entre os pontos n e n+1 é determinado pela equação:
, =
∆
∆
=
(eq. 3)
Devemos ressaltar que quando a aceleração é constante, a aceleração média e a aceleração
instantânea ( = ) são iguais. Portanto:
1 − ( ∙ " − #)
− = " − # + '
2 − (eq. 4)
, = " + #
)
Considerando que o móvel inicia seu movimento desde o repouso, com as equações podemos
calcular a velocidade instantânea da sequencia de pontos , ) , * , ... etc.
Figura 2. As posições do móvel são representadas como x1, x2, x3, x4 e x5.
4.
ATIVIDADE EXPERIMENTAL
Considerando o experimento do plano inclinado na figura xx, realize os seguintes passos:
4.1 Meça o ângulo de inclinação do trilho.
4.2 O experimentador deve realizar, no mínimo, cinco deslocamentos do móvel (x1, x2, x3, x4
e x5) e partindo do mesmo ponto, x0,veja tabela 01.
4.3 Para medição do tempo utilizado pelo móvel em cada posição xi (i = 1, 2, 3, 4, 5), a partir
de x0=0, os experimentos devem ser repetidos no mínimo cinco vezes. Desta forma
estaríamos reduzindo os erros inevitáveis na medição do tempo.
4.4 Calcule o valor médio do tempo, para cada deslocamento do disco, e seu respectivo erro.
4.5 A tabela 01 deve estar preenchida com todos os valores calculados.
4.6 Determine a velocidade media em diferentes deslocamentos (+, , ,) , ),* , *,, , e ,,-) e
preencha os valores calculados segundo descrito na tabela 02.
4.7 A partir da velocidade media obtida em cada intervalo, determine a velocidade
instantânea em x1, x2, x3, x4, x5. Apresente seus resultados de acordo com a tabela 03.
Física Experimental I
Prof. Robinson
4.8 Considerando as grandezas deslocamento (d) e seu respectivo tempo (t), cada um com
seu respectivo desvio padrão, faça o gráfico de x versus t.
4.9 Faça o gráfico x versus t2.
4.10 Determine a aceleração do disco.
5.
DISCUSSÃO E ALGUMAS QUESTÕES
5.1. DISCUSSÃO
5.1.1
Neste tipo de experimento, o experimentador teve controle dos erros em suas
medições?
5.1.2
O valor encontrado da aceleração da gravidade está de acordo com os valores
encontrado pelo pêndulo simples?
5.1.3
Se o corpo tivesse outra forma como seriam os resultados?
5.1.4
O ângulo de inclinação influencia o valor da aceleração do objeto? Explique.
5.1.5 Qual o significado físico da tangente de qualquer ponto da curva do gráfico x versus
t?
5.2. QUESTÕES
5.2.1
A velocidade de uma partícula que se encontra na posição 20m em t = 0, varia
segundo a tabela mostrada abaixo:
velocidade (m/s)
tempo (s)
30
10
50
12
70
14
90
16
Sendo o movimento retilíneo, determine:
(a) a aceleração; b) A velocidade e do espaço em função do tempo; (c) a velocidade em t =
50s; (d) a velocidade média entre 10s e 14s; (e) o instante em que a velocidade é 400 m/s
5.2.2
A velocidade de uma partícula aumenta de 36km/h para 108km/h em 5 segundos em
linha reta. Calcule:
(a) a sua aceleração; (b) a distância percorrida em 40 segundos desde o repouso; (c) a sua
velocidade em t = 25 segundos partindo do repouso; (d) o instante onde a sua velocidade é
50m/s
5.2.3
A velocidade de um móvel que parte da origem dos espaços e move-se em linha reta,
varia com o tempo segundo o gráfico v = f(t) abaixo.
Calcule:
Física Experimental I
Prof. Robinson
(a) a aceleração; (b) a velocidade em t = 30 segundos; (c) o instante em que a velocidade é
100 m/s;
d) a posição em t = 10 segundos; (e) a posição em t = 50s; (f) a distância percorrida entre t =
5 s e t = 20 s
6.
CONCLUSÕES
Coloque seus resultados finais.
7.
BIBLIOGRAFIA
[1]
Serway e Jewett, Principios de Física, Vol. 2, 3ª edição, Thomson Learning Edições Ltda,
2002.
Moyses Nussenzveig, Curso de Física Básica, Vol. 2, 4ª Edição, Editora Edgard Blucher,
2005.
Halliday e Resnick, Fundamentos de Física, Vol 2, 8ª Edição, Livros Técnicos e Científicos
Editora S.A., 2009.
[2]
[3]
Física Experimental I
Prof. Robinson
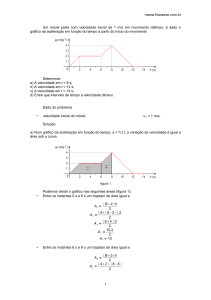
FOLHA DE DADOS EXPERIMENTAIS
Experimento 01: Teoria de Erros
UNIDADE 2 – CINEMATICA
Metodologia Experimental
Tabela 01: Dados
ados experimentais obtidos de um disco se deslocando no plano inclinado.
Distância
x0 = 0
x1 = 10 cm
x2 = 20 cm
x3 = 30 cm
x4 = 40 cm
x5 = 50 cm
t0=
t1=
t2=
t3=
t4=
t5=
t0=
t1=
t2=
t3=
t4=
t5=
Medida do tempo
[s]
t0=
t0=
t1=
t1=
t2=
t2=
t3=
t3=
t4=
t4=
t5=
t5=
Valor médio do
tempo
Erro da
medida
t0=
t1=
t2=
t3=
t4=
t5=
Tabela 02: Velocidade media em diferentes deslocamentos.
1º deslocamento
∆01= x1 – x0
x1 – x0
t1 – t 0
(m)
(s)
0,1.
.
2º deslocamento
∆12= x2 – x1
x2 – x1
t 2 – t1
(m)
(s)
0,1.
.
3º deslocamento
∆23= x3 – x2
x3 – x2
t3 – t 2
(m)
(s)
0,1.
.
4º deslocamento
∆34= x4 – x3
x4 – x3
t4 – t 3
(m)
(s)
0,1.
.
(m/s)
.
(m/s)
.
(m/s)
.
(m/s)
.
+, =
1− /
1 − /
,) =
2− 1
2 − 1
),* =
0− 2
0 − 2
*,, =
1− 0
1 − 0
5ºº deslocamento
∆45= x5 – x4
x5 – x4 (m)
t 5 – t4
(s)
0,1
0,1.
.
,, =
,
2− 1
2 − 1
(m/s)
.
móvel, calculado a partir da
Tabela 03: Dados de distancia, tempo e velocidade instantânea do móvel,
equação , = " + #.
)
Medida
Nº
0
1
2
3
4
5
Distância
(m)
x0 = 0
x1 = 10
x2 = 20
x3 = 30
x4 = 40
x5 = 50
Valor médio do
tempo
(s)
t0 = 0
t1 =
t2 =
t3 =
t4 =
t5 =
Velocidade
instantânea
(m/s)
v0 = 0
v1 =
v2 =
v3 =
v4 =
v5 =
Física Experimental I
Prof. Robinson
CURIOSIDADES
Qual é o animal mais rápido do planeta?
O guepardo (ou chita) é o mamífero mais rápido do mundo. Pode atingir
uma velocidade de 110 km/hora. Já o homem atinge um máximo de 43
km/hora.
ANIMAL
Guepardo
Antílope indiano
Leão
Gazela
Cavalo
Raposa
Zebra
Hiena
Coelho
Girafa
Veado nobre
Gato doméstico
Rinoceronte
Elefante
Pinguim
Porco
KM/HORA
110
98
80
80
75
67
65
65
55
50
48
48
45
40
37
17
Qual é o trem-bala mais rápido que existe?
Experimentalmente, um trem-bala da linha francesa TGV já chegou à velocidade máxima de 515
km/h. Na prática, porém, no dia-a-dia de viagens, o modelo que anda mais rápido vai de Lyon a
Aix-en-Provence a uma velocidade média de 263,3 km/h. Ele também é um TGV francês, sigla de
Train à Grande Vitesse - "Trem de Alta Velocidade". Andando a quase 300 km/h, os trens-bala são
um meio de transporte mais rápido que o avião para percorrer distâncias de até 650 quilômetros.
Apesar de os aviões voarem a cerca de 800 km/h, os passageiros perdem muito mais tempo para
embarcar num aeroporto do que numa estação de trem. Se houvesse um TGV entre Rio de Janeiro e
São Paulo, por exemplo, o tempo de viagem seria de 1 hora e 38 minutos. Um vôo entre as duas
cidades não chega a 1 hora, mas perde-se pelo menos uns 50 minutos nos procedimentos de checkin e embarque no aeroporto. Curiosamente, a tecnologia dos trens-bala não tem nada de espetacular.
Eles são puxados por uma espécie de locomotiva elétrica, da mesma forma que os metrôs, só que
abastecidos por correntes até nove vezes maiores. As linhas também são planejadas para alta
velocidade, apresentando poucas curvas, estações distantes entre si e ausência de tráfego de trens
mais lentos. O primeiro trem de alta velocidade foi o japonês Shinkansen, que estreou em 1964 na
linha Tóquio-Nagoya- Kyoto-Osaka.