RACIOCÍNIO LÓGICO DIAGRAMAS PROF PEDRÃO 1 } vogal éx/x

RACIOCÍNIO LÓGICO
DIAGRAMAS
PROF PEDRÃO
CONJUNTOS
É
um
agrupamento
de
elementos,
NÚMEROS RACIONAIS (Q)
e
são
Um número racional Q pode ser definido como:
representados por letras maiúsculas do alfabeto latino
Q
e seus elementos são dispostos entre chaves.
Ex: A = {vogais} = {a,e,i,o,u}
Existem duas outras formas de representação:
Z
Z*
Portanto, nos números racionais, além dos
inteiros, estão as “frações” e os decimais obtidos
como resultado das mesmas (exatos e não exatos
Compreensão
A
periódicos).
NÚMEROS IRRACIONAIS (I)
{ x / x é vogal}
Diagramas
São os decimais não exatos e não periódicos.
Ex:
3,14 , e
2,7 , 2
1,4 , 3
1,7
NÚMEROS REAIS (R)
Ao “juntarmos” os números racionais (Q) com os
irracionais (I), obtemos o conjunto dos números reais
(R).
CONJUNTOS NUMÉRICOS
Por diagramas:
NÚMEROS NATURAIS (N)
São aqueles que a “natureza” nos ensina:
N = {0, 1, 2, 3, 4, 5,...}
NÚMEROS INTEIROS (Z)
PERTINÊNCIA ( ou
)
São os Naturais e seus opostos:
Z = {..., –3, –2, –1, 0, 1, 2, 3,...}
Obs: Z* = números inteiros menos o zero
A pertinência (pertence ou não pertence) será
utilizada quando relacionarmos elemento e conjunto.
Z+ = inteiros não negativos
SUBCONJUNTO (
(Z+ = {0, 1, 2, 3,...})
ou
e
ou
)
Z – = inteiros não positivos
(Z – = {...,–3,–2,–1,0})
Quando a relação for entre conjuntos, diremos
que um conjunto está ou não contido em outro, ou
ainda que um conjunto contém ou não outro.
O número de subconjuntos de um conjunto é
n
dado por 2 , onde n é o número de elementos do
conjunto
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
1
RACIOCÍNIO LÓGICO
DIAGRAMAS
PROF PEDRÃO
EXERCÍCIOS
INTERSECÇÃO (
)
Consideramos apenas os elementos “em comum”.
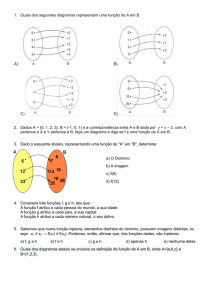
01) Dado o conjunto A = { 1,2,3,{3},4}, complete os
Por diagramas:
A
espaços em branco a seguir:
a) 1
B
A
b) {2}
c) 3
A
A
d) {3}
A
e) {{3}}
f) A
A
A
g) A
02) Seja o conjunto A = {0, {0}, 1, {1}, {0, 1}}
É correto afirmar que:
a) 0
A
DIFERENÇA (–)
b) {0,1}
A
c) {0,1}
A
São os elementos que “aparecem” no primeiro
conjunto e que “não aparecem” no segundo conjunto.
d) os elementos de A são 0 e 1
Por diagramas:
e) o número de subconjuntos de A é 22 = 4
A–B
OPERAÇÕES ENTRE CONJUNTOS
UNIÃO (U)
Como o próprio nome diz: vamos unir os
conjuntos, ou seja, “juntar” os elementos dos dois
conjuntos.
Obs: Quando houver elementos repetidos, apenas
um deles “aparecerá” no conjunto.
Por diagramas:
EXERCÍCIOS
03) Sejam os conjuntos:
A
x N/3
x 8
B
x R/3 x 8
e
Assinale o que for correto.
2
2009
a )A
B
b )A
B
c )A
B
d )A
B
B
e )A
B
A
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
RACIOCÍNIO LÓGICO
DIAGRAMAS
04) Em uma turma de 60 alunos, 21 praticam natação
05) 120
e futebol, 39 praticam natação e 33 praticam futebol.
06) 26 000
a)Qual a porcentagem de alunos que praticam um, e
07) 300
PROF PEDRÃO
somente um, desses esportes?
b)Qual a porcentagem de alunos que não praticam
DIAGRAMAS LÓGICOS
nenhum desses esportes?
O estudo da Teoria dos Conjuntos e dos
05) Na escola do professor Golias, são praticadas
Diagramas de Venn são ferramentas importantes na
duas modalidades de esportes: o futebol e a natação.
resolução de questões de Raciocínio Lógico, sendo
Exatamente 80% dos alunos praticam futebol e 60%,
que devemos destacar três situações:
natação. Se a escola tem 300 alunos e todo aluno
pratica pelo menos um esporte, então o número de
alunos que praticam os dois esportes é:
Conjuntos que não possuem elementos em
comum (disjuntos – (A
B
) – “Nenhum A é
B”
06) Em uma cidade com 40.000 habitantes há três
clubes recreativos: Colina, Silvestre e Campestre.
Feita uma pesquisa, foram obtidos os seguintes
resultados: 20% da população freqüenta o Colina;
16% o Silvestre; 14% o Campestre; 8% o Colina e o
Silvestre; 5% o Colina e o Campestre; e 4% o
Silvestre e o Campestre. Somente 2% freqüentam os
três clubes. O número de habitantes que não
Conjuntos
que
possuem
elemento em comum (A
freqüentam nenhum destes três clubes é:
B
ao
menos
um
) – “Algum A é B”
e “Algum A não é B”
07) Um instituto de pesquisas entrevistou 1.000
indivíduos, perguntando sobre sua rejeição aos
partidos A e B. Verificou-se que 600 pessoas
rejeitavam o partido A; que 500 pessoas rejeitavam o
partido B e que 200 pessoas não tem rejeição alguma.
O número de indivíduos que rejeitam os dois partidos
é:
Conjunto contido em outro conjunto (A
GABARITO
01) a)
“Todo A é B”
b)
c)
e)
f)
03) a) V
b) F
c) V
d) V
e) V
d)
ou
B) –
ou
g)
02) b)
04) a) 50%
2009
b) 15%
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
3
RACIOCÍNIO LÓGICO
DIAGRAMAS
PROPOSIÇÕES CATEGÓRICAS
PROF PEDRÃO
PRINCIPAIS NEGAÇÕES
# Todo A é B (V), então:
Nenhum A é B (F)
"TODO É"
"PELO MENOS UM NÃO"
"EXISTE UM QUE NÃO É"
"ALGUM NÃO É"
"NENHUM É"
"PELO MENOS UM É"
"EXISTE UM QUE É"
"ALGUM É"
"ALGUM É"
"NENHUM É"
Algum A é B (V)
Algum A não é B (F)
# Nenhum A é B (V), então:
Todo A é B (F)
Algum A é B (F)
Algum A não é B (V)
"ALGUM NÃO É" "TODO É"
# Algum A é B (V), então:
Nenhum A é B (F)
Todo A é B (indeterminada)
Algum A não é B (indeterminada)
A negação da frase: "Todo Gremista é
inteligente" é:
"Pelo menos um Gremista não é inteligente"
"Existe um Gremista que não é inteligente "
"Algum Gremista não é inteligente "
# Algum A não é B (V), então:
Todo A é B (F)
Nenhum A é B (indeterminada)
Algum A é B (indeterminada)
# Todo A é B (F)
Algum A não é B (V)
Nenhum A é B (indeterminada)
A negação da frase: "Nenhum Gremista é
inteligente " é
"Pelo menos um Gremista é inteligente "
"Existe um Gremista que é inteligente "
"Algum Gremista é inteligente "
A negação da frase: "Algum Gremista é
inteligente " é
Algum A é B (indeterminada)
"Nenhum Gremista é inteligente "
# Nenhum A é B (F)
A negação da frase: "Algum Gremista não
é inteligente " é
Algum A é B (V)
Todo A é B (indeterminada)
Algum A não é B (indeterminada)
"Todos Gremistas são inteligente "
# Algum A é B (F)
Todo A é B (F)
Nenhum A é B (V)
Algum A não é B (V)
# Algum A não é B (F)
Todo A é B (V)
Nenhum A é B (F)
Algum A é B (V)
4
2009
Neste curso os melhores alunos estão sendo preparados pelos melhores Professores
This document was created with Win2PDF available at http://www.win2pdf.com.
The unregistered version of Win2PDF is for evaluation or non-commercial use only.
This page will not be added after purchasing Win2PDF.