Lista 2 - Prof. Benfica

Data:
Série:
LISTADEEXERCÍCIOS
OlimpíadasCientíficas
Prof.MarcosBenfica
MRUVeLançamentos
1.(Ime2016)
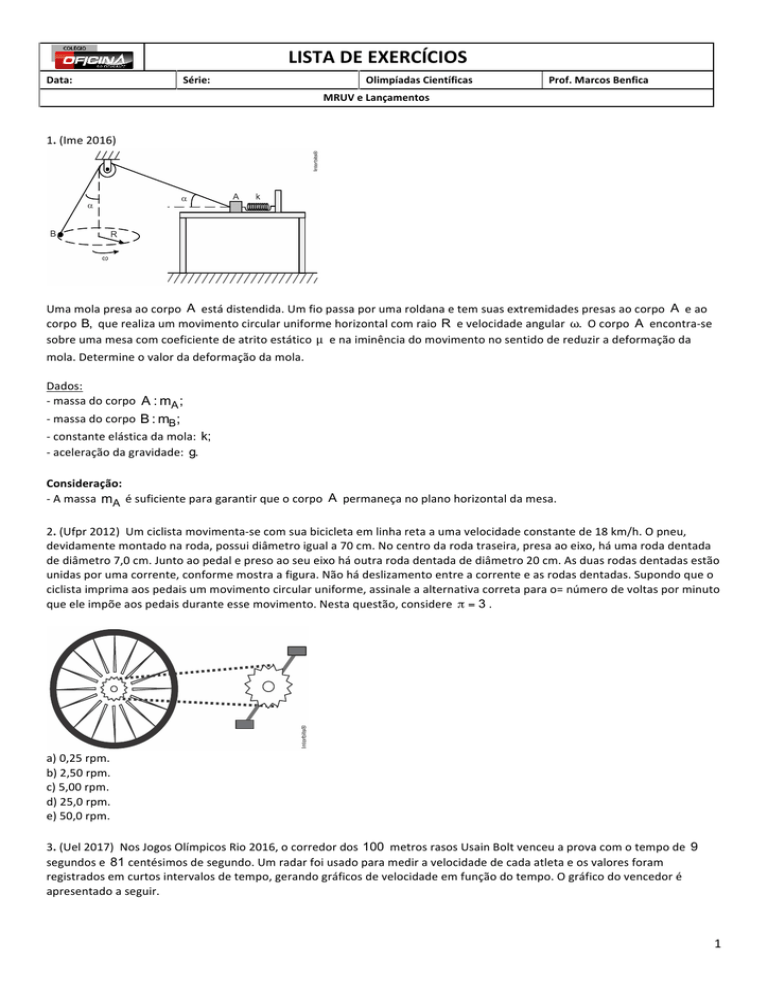
Umamolapresaaocorpo A estádistendida.Umfiopassaporumaroldanaetemsuasextremidadespresasaocorpo A eao
corpo B, querealizaummovimentocircularuniformehorizontalcomraio R evelocidadeangular ω. Ocorpo A encontra-se
sobreumamesacomcoeficientedeatritoestático µ enaiminênciadomovimentonosentidodereduziradeformaçãoda
mola.Determineovalordadeformaçãodamola.
Dados:
-massadocorpo A : mA ; -massadocorpo B : mB ; -constanteelásticadamola: k; -aceleraçãodagravidade: g. Consideração:
-Amassa mA ésuficienteparagarantirqueocorpo A permaneçanoplanohorizontaldamesa.
2.(Ufpr2012)Umciclistamovimenta-secomsuabicicletaemlinharetaaumavelocidadeconstantede18km/h.Opneu,
devidamentemontadonaroda,possuidiâmetroiguala70cm.Nocentrodarodatraseira,presaaoeixo,háumarodadentada
dediâmetro7,0cm.Juntoaopedalepresoaoseueixoháoutrarodadentadadediâmetro20cm.Asduasrodasdentadasestão
unidasporumacorrente,conformemostraafigura.Nãohádeslizamentoentreacorrenteeasrodasdentadas.Supondoqueo
ciclistaimprimaaospedaisummovimentocircularuniforme,assinaleaalternativacorretaparao=númerodevoltasporminuto
queeleimpõeaospedaisduranteessemovimento.Nestaquestão,considere π = 3 .
a)0,25rpm.
b)2,50rpm.
c)5,00rpm.
d)25,0rpm.
e)50,0rpm.
3.(Uel2017)NosJogosOlímpicosRio2016,ocorredordos 100 metrosrasosUsainBoltvenceuaprovacomotempode 9 segundose 81 centésimosdesegundo.Umradarfoiusadoparamediravelocidadedecadaatletaeosvaloresforam
registradosemcurtosintervalosdetempo,gerandográficosdevelocidadeemfunçãodotempo.Ográficodovencedoré
apresentadoaseguir.
1
Considerandoográficode V versus t, respondaaositensaseguir.
a)CalculeaquantidadedemetrosqueBoltpercorreudesdeoinstante 2,5 s atéoinstante 4,5 s, trechonoqualavelocidade
podeserconsideradaaproximadamenteconstante.
b)CalculeovaloraproximadodaaceleraçãodeUsainBoltnosinstantesfinaisdaprova,ouseja,apartirde 9 s. TEXTOPARAAPRÓXIMAQUESTÃO:
Considereomódulodaaceleraçãodagravidadecomo g = 10,0 m s2 eaconstantedagravitaçãouniversalcomo
G = 6,7 × 10−11 m3 kg−1 s−2 eutilize π = 3. 4.(Upe-ssa12017)Emumtreinodecorrida,avelocidadedeumatletafoiregistradaemfunçãodotempo,conformeilustraa
figuraaseguir.
Adistânciatotalpercorridapelocorredor,emmetros,duranteoperíododetempoemqueelepossuíaaceleraçãodiferentede
zero,é
a) 4 b) 7 c) 8 d) 14 e) 22 5.(G1-ifce2016)Avelocidadehorizontalmínimanecessáriaparaumapessoapulardoponto X eatingiroponto Y, como
mostraafiguraabaixo,deveserde
2
(Desprezearesistênciadoareconsidereaaceleraçãodagravidadecomosendo g = 10 m s2 ) a) 1m s. b) 5 m s. c) 4 m s. d) 8 m s. e) 9 m s. 6.(Ita2016)Apartirdorepouso,umfoguetedebrinquedoélançadoverticalmentedochão,mantendoumaaceleração
constantede 5,00 m s2 duranteos 10,0 primeirossegundos.Desprezandoaresistênciadoar,aalturamáximaatingidapelo
fogueteeotempototaldesuapermanêncianoarsão,respectivamente,de
a) 375 m e 23,7 s. b) 375 m e 30,0 s. c) 375 m e 34,1s. d) 500 m e 23,7 s. e) 500 m e 34,1s. 7.(Fac.AlbertEinstein-Medicin2017)Namodalidadeesportivadosaltoàdistância,oesportista,parafazeromelhorsalto,
deveatingiravelocidademáximaantesdesaltar,aliando-aaomelhorângulodeentradanomomentodosaltoque,nessa
modalidade,éo 45°. Considereumasituaçãohipotéticaemqueumatleta,nomomentodosalto,alcanceavelocidadede
43,2 km h, velocidadepróximadorecordemundialdos 100 metrosrasos,queéde 43,9 km h. Desprezeoatritocomoar
enquantoeleestáem“vôo”econsidereosaltadorcomoumpontomaterialsituadoemseucentrodegravidade.
Nessascondições,qualseria,aproximadamente,adistânciaalcançadanosalto?
Adoteomódulodaaceleraçãodagravidadeiguala 10 m s2 . Dados: sen 45° = cos 45° = 0,7 a) 7 m b) 10 m c) 12 m d) 14 m 8.(Ufpr2017)NasParalimpíadasrecentementerealizadasnoBrasil,umadasmodalidadesesportivasdisputadasfoio
basquetebol.Emumdeterminadojogo,foiobservadoqueumjogador,parafazeracesta,arremessouabolaquandoocentro
demassadessabolaestavaaumaalturade 1,4 m. Otempotranscorridodesdeoinstanteemqueaboladeixouamãoao
jogadoratéteroseucentrodemassacoincidindocomocentrodoarofoide 1,1 s. Nomomentodolançamento,ocentrode
3
massadabolaestavaaumadistânciahorizontalde 4,4 m docentrodoarodacesta,estandoessearoaumaalturade 3,05 m,
conformepodeserobservadonafiguraaseguir.
Considerandoqueamassadabolaéiguala 600 g, quearesistênciadoarédesprezívelequeovalorabsolutodaaceleração
gravidadeéde 10 m s2 , determine,utilizandotodasasunidadesnoSistemaInternacionaldeUnidades:
a)Avelocidadehorizontaldabolaaoatingirocentrodoarodacestadebasquete.
b)Avelocidadeinicialverticaldabola.
c)Aenergiacinéticadabolanomomentodolançamento(considerandooexatoinstanteemqueaboladeixaamãodoatleta).
Gabarito:
Respostadaquestão1:
kΔx = µ ⋅ mA g − mBω2R + mBg ⇒ Δx =
(
)
1 ⎡
⋅ µ ⋅ mA g − mBω2R + mBg⎤⎥ ⎦
k ⎢⎣
(
)
Respostadaquestão2:
[E]
Respostadaquestão3:
a)20,8m.
2
b)–8,2m/s .
Respostadaquestão4:
[D]
Respostadaquestão5:
[B]
Respostadaquestão6:
[A]
Respostadaquestão7:
[D]
Respostadaquestão8:
a)4m/s
b)7m/s.
c)19,5J.
4