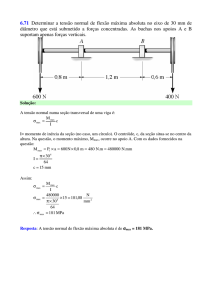
SALA: 68- C Animais
Cálculo Diferencial e Integral 2
Quarta Feira
4a Aula
Aplicações de Integrais Definidas:
Centróide e Volume
Turma: BCT
Prof. Walter Martins
Versão: 2o Semestre de 2010
Prof. Walter Martins
Notas de aula
Calculo 2
Aplicações das Integrais Definidas
A integral definida para cálculo do Centróide
O problema de determinar o centróide de uma região planar (R) é definido como
o centro de massa da região. O centro de massa é o ponto pelo qual esta região R pode
ser suspensa sem girar. As coordenadas ( x , y ) do centróide são dadas por
x
1 2
x [ f ( x) g ( x)] x dx
A x1
x
1 2 2
y
[ f ( x) g 2 ( x)] dx
2 A x1
Exemplo: Achar as coordenadas do centróide da região limitada pela curva y2 = 2x e
o eixo x, no intervalo [0,3].
y
y2 = 2x
y=
1
2
3
2x
(só a parte positiva)
x
Solução: Acha-se a área A
3
A
3
3
2 x dx 2 x
0
1/ 2
0
x
3
xA
27
3 3
x3 / 2
dx 2
2 2
2 6
2 2
3
3
3 2 0
2 x 0 dx
3
2
0
3
yA=
0
x
0
y2
2 0
2x
3
1
dx =
2
18
6
18
5
x =
=
= 1,8
10
2 6
0
3/ 2
dx
18
6
5
2
2 x dx = 1 . 2 . x
2
2
y =
3
=
0
9/2
2 6
=
9
2
9
= 0,92
4 6
1
Prof. Walter
Assunto: Centróide
Exemplo: Determinar o centróide da figura entre as duas curvas y x 3 e y x .
y x3
Y
(1,1)
y
x
X
1
A
x x 3 dx
0
1
xA x
5
12
x x 3 dx
0
1
5
1
1
1
1 x2 x7
1 1 1 1 7 2
5
6
yA x x dx
20
2 2
7 0 2 2 7 2 14
28
x
2
5 12 0,48
5
25
12
5
5 12
3 4
12
3
=
=
= = 0,43
y = 28 =
5
28
7
5 28
47
12
Exemplo: Determinar o centróide de uma semicircunferência positiva.
Solução:
A equação da circunferência e x 2 y 2 r 2 , onde r raio . Então, y r 2 x 2 é a
semicircunferência.
Y
y r 2 x2
r
r
X
2
Prof. Walter Martins
A
Notas de aula
Calculo 2
r2
2
u r 2 x2
du
dx
2x
du 2 xdx
r
xA
x
r 2 x 2 dx
r
r
xA x . u
r
1/ 2
r
x
2
2 r 2
du
1
1 2u 3 / 2
1/ 2
.
u du
2x
2 r
2 3
4 x
r
2 3
r
1 2
r r2
r 2
3
r
2
r
r
u3/ 2
3
r
r
3
r 2 0 ,
como já era esperado.
r
r
1
1
x3
1
r3
r3
r 3 2r 3
yA r 2 x 2 dx r 2 x r 3
r 3 r 3
2 r
2
3 r 2
3
3
3
3
y
2 2r 3 4 r
3
r2 3
Exercício:
Calcule o centróide de uma semicircunferência. A equação da
circunferência e x2 + y2 = r2 , onde r = raio, r = 2. Então y =
semicircunferência.
4 x2
é a
Y
y 4 x2
2
2
X
r2 4
A
2
2
2
2
xA
x
2
4 x dx
2
u 4 x 2
du
du 2 xdx
dx
2x
3
Prof. Walter
Assunto: Centróide
2
x .u
2
1/ 2
2
du
1
1 2u 3 / 2
1/ 2
.
u du
2x
2 2
2 3
4 x
1
2
2
2
u 3/ 2
3
2
2
2
2 3
0 (como já era esperado)
2
4 x
2
1
yA =
2
yA =
2
2
16
3
2
3
dx = 1 4 x x = 1 8 8 8
3 2 2
2
3
16
16
16
=
= 0,8488
y = 3 =
3A
6
A
8 16
=
3 3
Exercício: Determinar o centróide da área delimitada pelas parábolas y 2 20 x ,
x 2 4 y 16 0 e o eixo X .
x 2 4 y 16 0
y
16 x 2 16 x 2
x2
4
4
4
4
4
Y
y f x
1
0
4
A
4
X
1
4
x2
x3
64
64
4
dx 4 x
16
16
4
12 4
12
12
A 32
32 96 32 64
3
3
3
4
4
4
3
x2
3
x3
3 2 x4
2x
x
x
4
dx
4
x
dx
64 4
4
64 4
4
64
16 4
4
3
44
2
24 2
x
2 4
64
16
16
4
0 (como já era esperado)
4
Prof. Walter Martins
4
x2
3
2
2
y
4
2
x
128 4
4
Notas de aula
2
4
3
dx
128 4
Calculo 2
x4
2
16
2
x
dx
16
4
3
2x3 x5
3
128 1024
128 1024
y
64
64
16 x
128
3
80 4 128
3
80
3
80
y
3
256 2048
256 768
3 53 8
128
3
32
1,6
128
3
80
128 1280
5
5
5
Aplicações das Integrais Definidas
Volume de sólidos de revolução
Uma região tridimensional (S) que possui as propriedades (a) e (b) a seguir é um sólido:
a) A fronteira de S consiste em um número finito de superfícies lisas que se
interceptam num número finito de arestas que por sua vez, podem se interceptar
num número finito de vértices.
b) S é uma região limitada.
Sólidos de Revolução - Método do Disco
Dada uma região R plana e uma linha reta, ou eixo, que pode tocar (a) ou não (b) em
R e que esteja no mesmo plano de R . Girando-se R em torno deste eixo, forma-se um
região no espaço tridimensional denominada sólido de revolução.
a)
S
R
Área plana
Sólido gerado pela Rotação.
5
Prof. Walter
Assunto: Centróide
b)
S
R
Área plana
Sólido gerado pela Rotação.
Girando o gráfico de uma função f x tem-se:
Y
r f x y
y f x
Y
dV r 2 dx
2
dV f x dx
Área plana
a
X
b X
V f x dx
b
2
a
a
b
Cálculo do elemento de volume
Exemplo: Usando o método do disco circular, calcule o volume do sólido gerado pela
revolução da região sob a função y f x x 3 , no intervalo 1, 2 .
(2,8)
Y
(2,8)
y x3
(1,1)
(1,1)
R
1
Área plana
r
x
2X
Elemento de volume
6
Prof. Walter Martins
2
2
Notas de aula
2
V [ f ( x)] dx [ x ] dx x 6 dx
2
3 2
1
1
1
Calculo 2
2 7 17 127
x7 2
18,143 56,99 u.v.
7 1
7
7 7
Exemplo: Achar o volume gerado pela função f x a 2 x 2 em a, a
Y
Y
y a2 x2
a
X
a
X
Sólido gerado pela rotação do
semi-círculo
Semi-círculo em rotação
2
x3 a
V [ f ( x)] dx [ a x ] dx [a x ]dx a x
3 a
a
a
1
a
a
2
2
2
2 2
2
2
3 2a 3
a3
a 3
a3
a3
V a 3 a 3 a 3
a3
2a
3
3
3
3
3
6a 3 2a 3 4
3
V
a
3
3
que é o volume da esfera gerada!
Exemplo: Uma região plana pode ser girada em torno do eixo y ao invés do eixo x , e
novamente um sólido de revolução será gerado.
7
Prof. Walter
Assunto: Centróide
y
y
b
r = x = g(y)
x = g(y)
R
dy
dV
x
a
x
Área plana girando em y
Sólido de revolução da área plana em
torno de y
b
b
V = [g( y)] 2 dy = r 2 dy
a
que é o volume do sólido
a
Exemplo: Calcule o volume gerado pela parábola y = x2 girando em torno do eixo de
y, no intervalo [0,4].
y
y
x= y
4
y = x2
0
2
x
x
Sólido gerado pela Parábola de revolução
Seção plana parábola girando em y
b
b
4
4
V [ g ( y)] 2 dy r 2 dy [ y ]2 dy ydy
a
a
0
0
y 2 4
2 0
42
0 8
2
V 8 25,13 u.v.
8
Prof. Walter Martins
Notas de aula
Calculo 2
O Método do Disco pode ser estendido para o Método dos Anéis Circulares. Este
método surge quando a área de revolução é limitada por duas funções f(x) e g(x), tal que
f(x) > g(x), para todo x[a,b].
y
f(x)
y
Anel projetado
dx
g(x)
g(x)
x
a
b
x
f(x)
Área plana em revolução
dV
Sólido gerado pela revolução
O elemento de volume do anel é dado por:
dV f x dx g x dx
2
2
f x
2
g x dx
2
de forma que o volume todo é dado por:
b
b
a
a
V dV [ f ( x)] 2 [ g ( x)] 2 dx
Note que o vão interno é descontado pela subtração dos dois volumes.
Exemplo: Calcular, usando o método dos anéis circulares, o volume formado pela
rotação da região entre y x 2 e y x 2 .
y x2
Y
(-1,1)
(2,4)
Y
R
X
X
Área entre parábola e reta.
Sólido de revolução
9
Prof. Walter
Assunto: Centróide
Solução: Faz-se f x x 2 e g x x 2 (pois f x g x )
Pontos de Interseção: f x g x x 2 x 2 , isto é:
x 1 y1 1
x2 x 2 0 1
x2 2 y 2 4
b
2
a
1
2
V dV ( x 2) 2 ( x 2 ) 2 dx ( x 2 4 x 4) ( x 4 ) dx
1
x 3 4x 4
x5
V x 4 x 4 x dx
4 x
2
5
3
1
2
2
4
2
1
2 3
2 5 (1) 3
(1) 5
2
2
V 2.2 4.2
2(1) 4(1)
3
5
3
5
8
8
32 1
1
32 1
1
V 8 8 2 4 16 2
5 3
5
5 3
5
3
3
40 240 96 5 30 3
184 32
216 72
V
15
15
15
5
15 15
logo V
72
45,2389 u.v.
5
Exercício: Se a revolução for em torno do eixo y, como por exemplo para as funções
x f y e x g y , tem-se:
dV [ f ( y)] 2 [ g ( y)] 2 dy
Y
x f y
Y
x gy
dy
dV
X
Área entre curvas, em
revolução
X
Sólido gerado pela área em
revolução
de forma que o volume todo é dado por:
10
Prof. Walter Martins
b
b
a
a
Notas de aula
Calculo 2
V dV [ f ( y)] 2 [ g ( y)] 2 dy
As vezes, o sólido de revolução é gerado em torno de um eixo externo que pode ser
paralelo a " x " ou a " y ". O método dos anéis circulares, pode ser aplicado, desde que se
identifique o raio do giro.
Exercício: Achar o volume do sólido gerado pela revolução da região R em torno do
eixo x 6 . R é limitada pelos gráficos de y 2 4 x e x 4 .
6 y2 4
Y
6 y2 4
4, 4
Y
dV
dy
R
6
X
x y2 4
4, 4
y 2 4x
6
Parábola girando em torno de um
eixo externo
Parabolóide gerado pela rotação
Solução: Para isolar-se x faz-se: y 2 4 x x
Também, se tem que: se x 4
2
y2
.
4
y 2 4 4 16 y 4
Observação: re raio externo 6 y 2 4 e ri raio interno 2
V
y 4
4
dV re2 ri 2 dy
y 4
4
11
Prof. Walter
Assunto: Centróide
2
4
4
y4
y2
y4
2
2
V 6 2 dy 36 3 y
4dy 3 y 2 32dy
4
16
16
4
4
4
4
y5
4
45
(4) 5
3
3
V y 32 y
4 32 4
(4) 3 32(4)
80
4
80
80
384 384 768
V
153,6 482,548 u.v. (unidades de volume)
5
5 5
12