SLC543 Física I (2002) – Prof

FCM0101 Física I (2015) – Prof. Javier
Lista 2: Vetores - Movimento em varias Dimensões
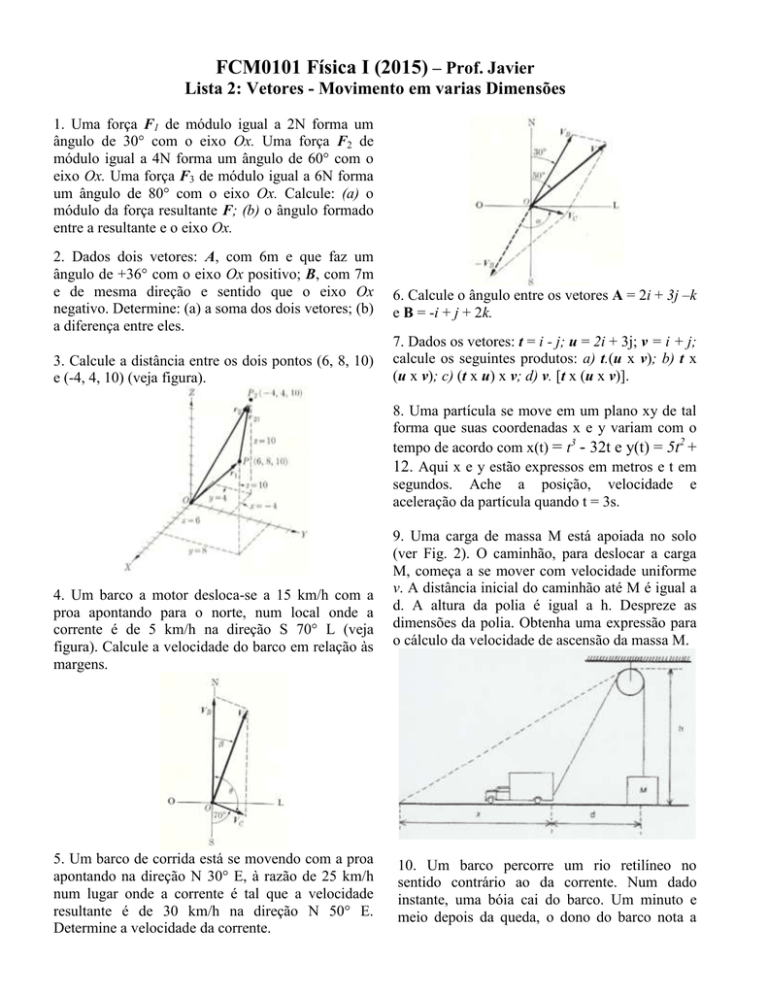
1. Uma força F1 de módulo igual a 2N forma um
ângulo de 30° com o eixo Ox. Uma força F2 de
módulo igual a 4N forma um ângulo de 60° com o
eixo Ox. Uma força F3 de módulo igual a 6N forma
um ângulo de 80° com o eixo Ox. Calcule: (a) o
módulo da força resultante F; (b) o ângulo formado
entre a resultante e o eixo Ox.
2. Dados dois vetores: A, com 6m e que faz um
ângulo de +36° com o eixo Ox positivo; B, com 7m
e de mesma direção e sentido que o eixo Ox
negativo. Determine: (a) a soma dos dois vetores; (b)
a diferença entre eles.
3. Calcule a distância entre os dois pontos (6, 8, 10)
e (-4, 4, 10) (veja figura).
6. Calcule o ângulo entre os vetores A = 2i + 3j –k
e B = -i + j + 2k.
7. Dados os vetores: t = i - j; u = 2i + 3j; v = i + j;
calcule os seguintes produtos: a) t.(u x v); b) t x
(u x v); c) (t x u) x v; d) v. [t x (u x v)].
8. Uma partícula se move em um plano xy de tal
forma que suas coordenadas x e y variam com o
tempo de acordo com x(t) = t3 - 32t e y(t) = 5t2 +
12. Aqui x e y estão expressos em metros e t em
segundos. Ache a posição, velocidade e
aceleração da partícula quando t = 3s.
4. Um barco a motor desloca-se a 15 km/h com a
proa apontando para o norte, num local onde a
corrente é de 5 km/h na direção S 70° L (veja
figura). Calcule a velocidade do barco em relação às
margens.
5. Um barco de corrida está se movendo com a proa
apontando na direção N 30° E, à razão de 25 km/h
num lugar onde a corrente é tal que a velocidade
resultante é de 30 km/h na direção N 50° E.
Determine a velocidade da corrente.
9. Uma carga de massa M está apoiada no solo
(ver Fig. 2). O caminhão, para deslocar a carga
M, começa a se mover com velocidade uniforme
v. A distância inicial do caminhão até M é igual a
d. A altura da polia é igual a h. Despreze as
dimensões da polia. Obtenha uma expressão para
o cálculo da velocidade de ascensão da massa M.
10. Um barco percorre um rio retilíneo no
sentido contrário ao da corrente. Num dado
instante, uma bóia cai do barco. Um minuto e
meio depois da queda, o dono do barco nota a
ausência da bóia e volta para resgatá-la. A bóia é
resgatada a 900 m a jusante do ponto onde ela caiu.
Calcule a velocidade da corrente do rio.
11. Um esquiador está se movendo para baixo numa
rampa plana de uma montanha. A inclinação (nortesul) faz um ângulo de 10° com a horizontal. O vento
sopra do oeste e dá ao esquiador uma aceleração
lateral de 0,54 m/s2 (veja Fig. 3). O esquiador
começa a descer do lado noroeste do alto da rampa,
com uma componente de velocidade de 9,0 m/s para
baixo e zero na componente lateral. A rampa, sem
atrito, tem 125 m de comprimento e 25 m de largura.
(a) Onde o esquiador sairá da rampa? (b) Qual a
velocidade do esquiador nesse ponto? (Sugestão: A
aceleração gravitacional ao longo de um plano
inclinado de um ângulo  é a = gsen .)
13. Em um jogo de beisebol o rebatedor acerta a
bola à altura de 1,40 m acima do chão, de modo
que seu ângulo de lançamento é de 52,0° com a
horizontal. A bola cai na platéia, à distância de
12,0 m acima do início da arquibancada. A
inclinação da arquibancada é de 28,0° e os
primeiros assentos ficam a 109 m da base do
rebatedor. Calcule a velocidade com que a bola
foi lançada pelo bastão. (Ignore a resistência do
ar.)
14. A Lua órbita em tomo da Terra, fazendo uma
revolução completa em 27,3 dias. Considere que
a órbita seja circular e tenha raio de 238.000
milhas. Qual é o módulo da aceleração da Lua
em direção à terra?
15. Um satélite da Terra se move em órbita
circular, a 640 km acima da superfície terrestre.
O tempo de uma revolução é de 98,0 min. (a)
Qual é a velocidade do satélite? (b) Qual é o
módulo da aceleração do satélite em direção à
terra?
Respostas:
12. Um avião tem velocidade de 290 km/h e
mergulha sob o ângulo de 27° abaixo da horizontal e
solta uma peça metálica para enganar o radar. A
distância horizontal entre aquele ponto e o ponto
onde a peça atingirá o solo é de 700 m. (a) Quanto
tempo a peça ficou no ar? (b) Qual a altura do avião
quando a peça foi largada?
1. (a) 11,41N; (b) 65,3°
2. (a) módulo= 4,13m, ângulo= +121° com o eixo Ox
positivo; (b) módulo de 12,31m, ângulo= +196,5° com o
eixo Ox positivo
3. 10,77 Unidades
4. módulo= 14,1km/h, ângulo= N +19,4° E
5 . módulo= 10,74 km/h, ângulo= S +77,28° E
6.  = 96,3°
7. (a) 0; (b) v; (c) -5t; (d) 2
8. r = -69i+57j; v = -5i+30j; a =18i+10j
2
2 1/2
9. v= (d+x)v/[(d+x) +h ]
10. 5 m/s
11. (a) 17,0 m; (b) v= 22,5 m/s i + 4,3 m/s j.
12. (a) 9,8s; (b) 830m
13. 35m/s
2
14. 0,00271 m/s
2
15. (a) 7,49 km/s; (b) 8,00 m/s