Sistemas de Controle Digital

ADL 24
Cap 13
Sistemas de Controle Digital
Vantagens dos Computadores Digitais
O uso de computadores digitais na malha leva às seguintes vantagens sobre os
sistemas analógicos: (1) custo, (2) flexibilidade para realizar mudanças de projeto, e
(3) imunidade a ruído. Os sistemas de controle modernos requerem o controle
simultâneo de numerosas malhas — pressão, posição. velocidade e tensão, por
exemplo.
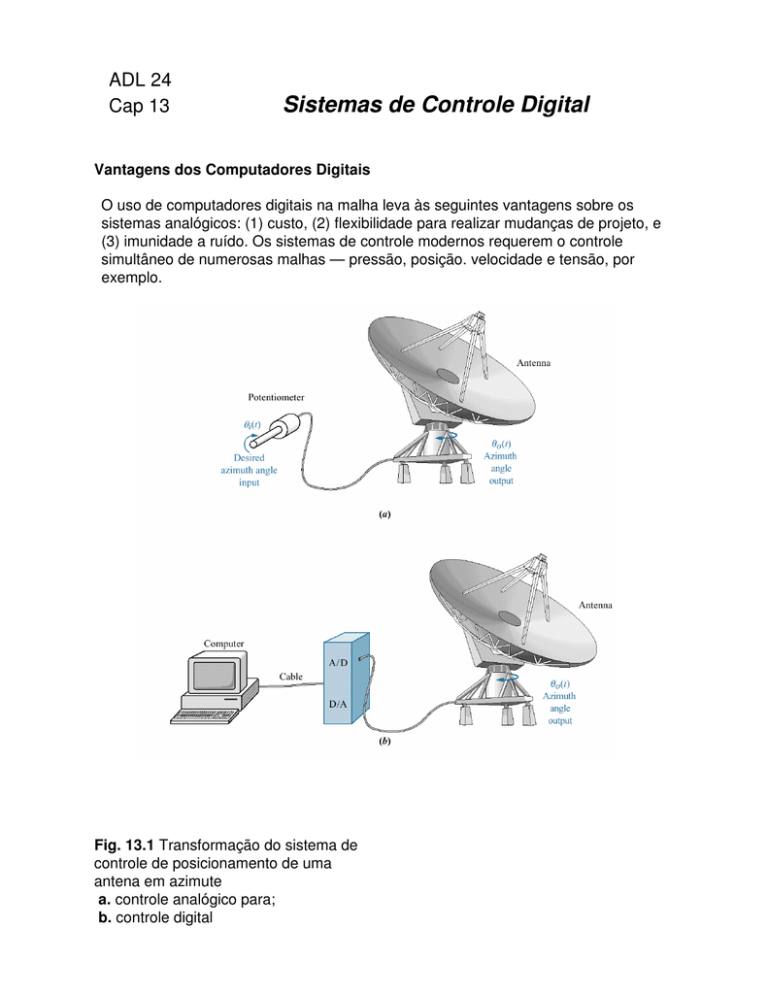
Fig. 13.1 Transformação do sistema de
controle de posicionamento de uma
antena em azimute
a. controle analógico para;
b. controle digital
Fig. 13.2
a. Posicionamento do computador digital na malha;
b. diagrama de blocos detalhado mostrando o posicionamento dos conversores
A/D e D/A
Conversão Digital-Analógica
A conversão digital-analógica é simples e efetuada de forma instantânea. Somamse tensões elétricas ponderada de forma adequada para produzir a saída
analógica. Por exemplo, na Fig. 13.3 são somadas três tensões pondera-das com
os pesos 1, 2 e 4. 0 código binário de três bits é representado pelas chaves.
Dessa forma, se o núm. binário for 110, as chaves do centro e inferior estão
ligadas, e a saída analógica é de 6 volts. Na tecnologia atual as chaves são
eletrônicas e acionadas pelo código binário de entrada.
Fig. 13.3 Conversor digital-analógico
Conversão Análogo-Digital
A conversão análogo-digital, por outro lado, é um processo de duas etapas e não é
instantâneo. Existe uma defasagem entre a tensão analógica de entrada e a palavra
digital de saída. Na conversão análogo-digital, o sinal análogo é primeiro convertido
em um sinal amostrado e depois transformado em uma seqüência de números
binários, o sinal digital.
A taxa de amostragem deve ser pelo menos duas vezes a banda passante do sinal, ou
ocorrerá distorção. Esta freqüência mínima de amostragem é chamada de taxa de
amostragem ou freqüência de Nyquist.
Etapas na conversão análogo-digital:
a. sinal analógico;
b. sinal analógico depois do amostrador-extrapolador de ordem zero (sample-and-hold);
c. conversão dos valores das amostras em valores digitais
13.2 Modelando o Computador Digital
Modelando o Amostrador
Considere os modelos de amostragem apresentados na Fig. 13.5. 0 modelo na Fig.
13.5(a) é uma chave ligando e desligando segundo uma taxa de amostragem
uniforme. Na Fig. 13.5(b) a amostragem também pode ser considerada como o
produto da forma de onda no domínio do tempo a ser amostrada. f(t), por uma
função de amostragem, s(t). Se s(t) for uma seqüência de pulsos de largura Tw,
amplitude constante e taxa uniforme, como mostrado, a saída amostrada, f*Tw(t),
consistirá numa seqüência de segmentos de f(t) nos intervalos regulares. Esta visão
é equivalente ao modelo de chave da Fig. 13.5(a).
Fig. 13.5 Duas vistas da amostragem com taxa uniforme:
a. abertura e fechamento da chave;
b.Produto do sinal no domínio tempo pelo sinal de amostragem
Usando o modelo mostrado na Fig. 13.5(b), temos
(13.1)
onde k é um número inteiro entre é a largura de cada pulso.
e + . T é o período do trem de pulsos, e Tw
Como a Eq. (13.1) é o produto de duas funções do tempo, aplicar a transformada
de Laplace para obter urna função de transferência não é simples. Uma
simplificação pode ser feita se admitirmos que a largura uniforme dos pulsos, Tw, é
pequena em comparação como período, T, de modo que f(t) possa ser considerada
constante durante o intervalo de amostragem. Durante o intervalo de amostragem.
Então, f(t) = f(kT). Portanto,
(13.2)
para Tw pequeno.
A Eq. (13.2) pode ser mais simplificada através da visão fornecida pela
transformada de Laplace. Aplicando a transformada de Laplace à Eq. (13. 2),
temos
(13.3)
Substituindo
por sua expansão em série, obtemos
(13.4)
Para Tw pequeno, a Eq. (13.4) se torna
(13.5)
Finalmente, retomando ao domínio de tempo, temos
(13.6)
onde
são funções delta de Dirac.
Por conseguinte, o resultado da amostragem com pulsos retangulares pode ser
vista como uma série de funções delta das quais a área é o produto da largura
do pulso retangular pela amplitude da forma de onda amostrada, ou seja,
Tw.f(kT).
A Eq. (13.6) é retratada na Fig. 13.6. 0 amostrador é dividido em duas partes:
(1) um amostrador ideal descrito pela parte da Eq. (13.6) que não é dependente
das características da forma de onda de amostragem e (2) a parte dependente
das características da forma de onda de amostragem, Tw
(13.7)
Fig. 13.6 Modelo de amostragem com trem de pulsos retangulares uniformes
Modelando o Extrapolador de Ordem Zero
Se admitirmos um amostrador ideal (equivalente a fazer Tw = 1), então f*(t) é
representada por uma seqüência funções delta. O extrapolador de ordem zero fornece
uma aproximação em escada para f(t) Portanto, a saída do extrapolador é uma
seqüência de funções degrau cuja amplitude é f(t) no instante de amostragem, ou
seja, f(kT). Uma vez que um impulso único do amostrador resulta em um degrau
durante o intervalo de amostragem, a transformada de Laplace deste degrau de saída,
Gh(s). que é a resposta do extrapolador ao impulso, é função de transferência do
extrapolador de ordem zero. Usando um impulso aplicado no instante zero, a
transformada do degrau resultante que inicia em t = 0 e termina em t = T é
(13.8)
Num sistema físico, os valores das amostras do sinal de entrada, f(kT), são mantidos
constantes durante o intervalo de amostragem. Podemos ver, com base na Eq.
(13.8), que o circuito extrapolador integra a entrada e retém seu valor durante o
intervalo de amostragem. Como a área sob as funções delta provenientes do
amostrador ideal é f(kT), podemos então integrar a forma de onda amostrada ideal e
obter o mesmo resultado obtido para o sistema fisico. Em outras palavras, se o sinal
amostrado ideal, f*(t), for seguido de um extrapolador, podemos usar a forma de
onda amostrada ideal como entrada, no lugar de
Fig. 13.7 Amostragem ideal e extrapolador de ordem zero (z.o.h.)
13.3 A Transformada z
A Eq. (13.7) é o sinal amostrado ideal. Aplicando a transformada de Laplace a este
sinal amostrado obtemos
(13.9)
Agora, fazendo z = eTs podemos escrever a Eq. (13.9) como
(13.10)
A Eq. (13.10) define a transformada z. Isto é, uma F(z) pode ser transformada
em. f(kT) ou uma f(kT), pode ser transformada em F(z)
Exemplo 13.1
Transformada z de uma função do tempo
Problema Determine a transformada z de uma rampa unitária
amostrada.
Solução Para a rampa unitária, f(kT) = kT. Portanto, o degrau
amostrado ideal pode ser escrito a partir da Eq. (13.7) como
(13.12)
Aplicando a transformada de Laplace obtemos
(13.13)
Aplicando a transformada z admitindo z-k = e-kTs temos
(13.14)
Multiplicando a Eq. (13.14) por z, obtemos
(13.15)
Subtraindo a Eq. (13.14) da Eq. (1.3.15), obtemos
(13.16)
Mas,
(13.17)
Substituindo a Eq. (13.17) na (13.16) e resolvendo para F(z), resulta
(13.18)
Tabela 13.1
Tabela parcial de transformadas z e de Laplace