EQUAÇÃES NORMALIZADAS PARA ANÊLISE DE CHOPPERS

EQUAÇÕES NORMALIZADAS PARA ANÁLISE DE CHOPPERS
APLICADOS EM ACIONAMENTOS
Kazuo Nakashima
Luiz E. B. da Silva
Valberto F. da Silva
Escola Federal de Engenharia de Itajubá
Departamento de Eletrônica
Abstract: This paper persents the normalized equations and graphics wich determine
the ripple of current and the limit of operations in the continous conduction mode of
pulse width modulated choppers.
Q1
D1
D2
I-INTRODUÇÃO
Q2
O chopper é um conversor estático que
converte diretamente uma tensão contínua
fixa em outra tensão contínua variável através da técnica de modulação em largura de
pulsos (PWM).
Como qualquer conversor estático o chopper é uma matriz de chaves eletrônicas
(diodos retificadores, tiristores, GTOs e transistores) que liga e desliga periodicamente a
carga na alimentação [1]. Este conversor
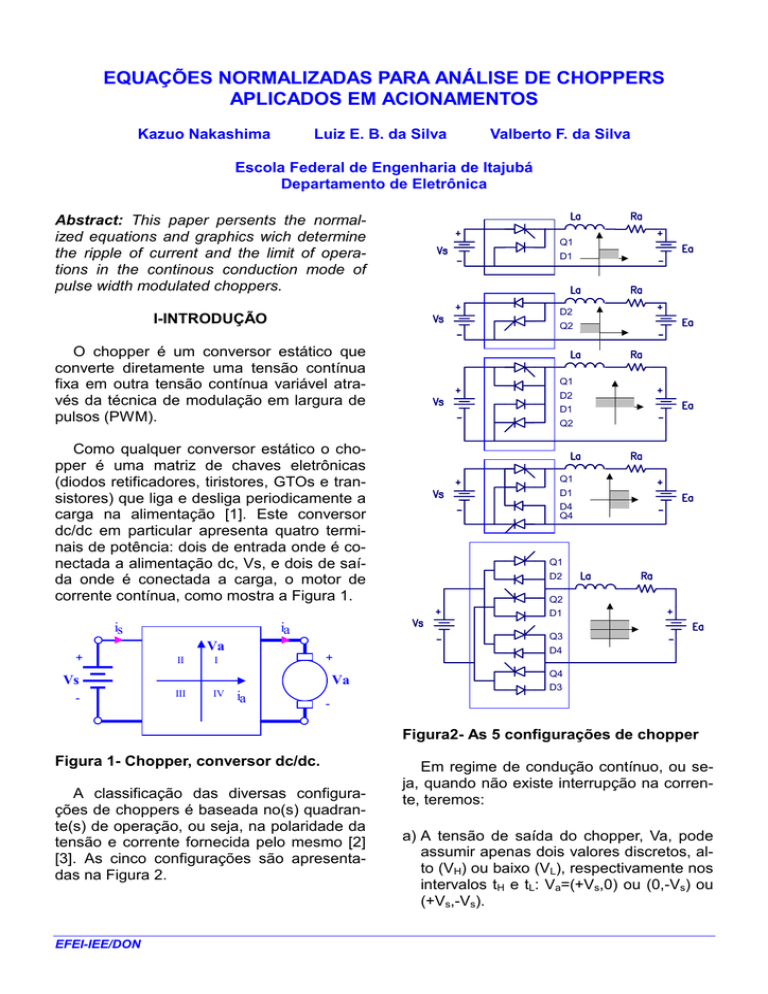
dc/dc em particular apresenta quatro terminais de potência: dois de entrada onde é conectada a alimentação dc, Vs, e dois de saída onde é conectada a carga, o motor de
corrente contínua, como mostra a Figura 1.
Q1
D2
D1
Q2
Q1
D1
D4
Q4
Q1
D2
Q2
D1
is
+
ia
Va
II
Q3
+
I
Vs
-
Va
III
IV
ia
D4
Q4
D3
-
Figura2- As 5 configurações de chopper
Figura 1- Chopper, conversor dc/dc.
A classificação das diversas configurações de choppers é baseada no(s) quadrante(s) de operação, ou seja, na polaridade da
tensão e corrente fornecida pelo mesmo [2]
[3]. As cinco configurações são apresentadas na Figura 2.
EFEI-IEE/DON
Em regime de condução contínuo, ou seja, quando não existe interrupção na corrente, teremos:
a) A tensão de saída do chopper, Va, pode
assumir apenas dois valores discretos, alto (VH) ou baixo (VL), respectivamente nos
intervalos tH e tL: Va=(+Vs,0) ou (0,-Vs) ou
(+Vs,-Vs).
Equações normalizadas para análise de choppers
b) Qualquer configuração de chopper pode
ser modelado em um dos três circuitos
equivalentes apresentados na Figura 3,
onde a carga (La, Ra e Ea) é o modelo de
uma máquina de corrente contínua de excitação independente.
c) Em regime permanente a corrente oscila
entre o pico mínimo Ia1 e o pico máximo
Ia2. No intervalo tH a tensão de saída Va
assume o valor alto (+Vs ou 0 dependendo da configuração) e a corrente de saída
aumenta de Ia1 para Ia2. No intervalo tL a
tensão de saída é baixo (0 ou -Vs) e a
corrente diminui de Ia2 para Ia1.
d) O valor médio da tensão na saída do
chopper, aplicada no motor, é função o ciclo de trabalho do chopper (duty cycle) d.
d = tH / (tH+tL) = tH / T
Va=(0; -VS)⇒Va(av)=(d-1).VS
Va=(-VS; +VS)⇒Va(av)=(2d-1)VS
La
Ea
X a (∞) = (1 − a )
Ea
Va=0
b)
X a (∞ ) = − a
Ea
Va= -Vs
X a (∞) = −(1 + a )
c)
VH
I a2
VL
tH
I a1
tL
Figura 3- Os três circuitos equivalentes e
as formas de onda de tensão e corrente.
EFEI-IEE/DON
I a(av) = [Va(av) - E a ] / R a
II-EQUAÇÃO NORMALIZADA
As equações do comportamento da corrente para os três circuitos equivalentes são:
va (t ) = vLa (t ) + vRa (t ) + Ea
[V]
d
va (t ) = La ia (t ) + Ra .ia (t ) + Ea [V]
dt
[A]
Va − Ea d
1
= ia (t ) + ia (t ) [A/s]
Ta .Ra
dt
Ta
T a=
Ra
Va=+Vs
a)
No modo de condução descontínuo a tensão no motor assume mais um valor durante
o intervalo onde a corrente é nula, Ea. O
cálculo do valor médio da tensão se torna
muito trabalhoso uma vez que devemos calcular este intervalo de tempo. Em ambos
casos, a corrente média no motor é:
Va − Ea
d
= Ta ia (t ) + ia (t )
Ra
dt
Va=(0; +VS)⇒Va(av)=d.VS
.2
La
Ra
(1)
(2)
(3)
(4)
[S]
(5)
VS..................Tensão de alimentação
Ra...............Resistência da armadura
La.................Indutância da armadura
Ea............................Tensão induzida
Ta..........Constante de tempo elétrica
T...Período de comutação do chopper
Tq....Período de comutação do tiristor
tH.................Intervalo de tempo "alto"
tL...............Intervalo de tempo "baixo"
ia(t)......Corrente de saída do chopper
Ia1................Pico inferior de corrente
Ia2..............Pico superior de corrente
Va..........Tensão de saída do chopper
[V]
[Ω]
[H]
[V]
[S]
[S]
[S]
[S]
[S]
[A]
[A]
[A]
[V]
A equação (4) é uma equação diferencial
de primeira ordem muito conhecida e apresenta uma solução do tipo
ia (t ) = I (∞) − [I (∞) − I (0)]ε −t / Ta
onde:
[A]
(6)
Equações normalizadas para análise de choppers
I (∞) =
Va − Ea
valor final
(7)
Ra
I (o) = I a1 ou I a 2 valor inicial
(8)
Ea = a . VS
Durante o intervalo tH o tiristor Q1 opera
como uma chave fechada e o diodo D1 como uma chave aberta resultando no circuito
equivalente apresentado na Figura 3(a).
Neste intervalo a corrente varia de Xa1 para
Xa2 tendendo ao valor final X(∞)=(1-a) segundo a Equação (10).
Va = +VS, 0 ou -VS.
xa (t )=(1 − a )−[(1−a )− X a1 ]ε −t / Ta
A equação (6) pode ser normalizada tomando-se como base:
No instante t=tH, (tH/Ta)=d.S, xa(tH)=Xa2
VB = VS
V
Ia = S
Ra
TB = Ta
[V]
tensão base
[A]
corrente base
[S]
tempo base
X a 2 =(1−a)−(1−a− X a1 )ε − d .S
obtendo:
xa (t )=[ X (∞ )− X (0)]ε −t / Ta
(9)**
onde as grandezas normalizadas, adimensionais, são:
xa (t ) =ia (t ) / I B ..........corrente no motor
X a1 = I a1 / I B ......pico inferior de corrente
X a 2 = I a 2 / I B ...pico superior de corrente
rpp = X a 2 − X a1 ......ondulação pico a pico
(10)
(11)
Durante o intervalo tL o tiristor Q1 é bloqueado forçando a circulação de corrente
via D1 resultando no circuito equivalente da
Figura 3(b). Neste intervalo a corrente é
mantida pela energia armazenada em La e
varia de Xa2 para segundo a equação (12) .
X(∝)=-a
xa (t ' )=(−a )−[(−a )− X a 2 ]ε −t ' / Ta
(12)
No instante t’=tL, tL/Ta=(1-d)S, xa(tL)=Xa1
X a1 =− a +(a + X a 2 )ε −(1−d ) S
(13)
t '=t −t H
(14)
X a (∞) =(1−a),− a,− (1+a ) .......valor final
X (0) = X a1 ou X a 2 ...................valor inicial
Resolvendo (11) e (13) obtemos (15) e (16)
a = Ea / Vs ......................tensão induzida
X a1 =
ε d .S −1
−a
ε S −1
S =T / Ta ..............período de comutação
d =t H / T ....ciclo de trabalho do chopper
d q =ton / Tq ...ciclo de trabalho do tiristor
III-CHOPPER CLASSE A (Q1)
Este chopper, apresentado na Figura 2(a),
o
opera apenas no 1 quadrante e a MCC opera apenas como motor, modo tração, para
Ea> 0.
EFEI-IEE/DON
.3
X a2 =
1− ε − d .S
1−ε − S
−a
(15)
(16)
A ondulação pico a pico da corrente no
regime de condução contínuo, rpp = (Xa2Xa1), é obtida pela Equação (17) cuja solução gráfica e apresentada na Figura 4(a).
1−ε − dS ε d .S −1
−
r pp =
1− ε − S ε S −1
(17)
Equações normalizadas para análise de choppers
A ondulação máxima rppmax ocorre para
d=0,5 e pode ser obtida pela Equação (18)
cuja solução gráfica á apresentada na Figura 4(b).
r pp max
[ε
=
0 ,5 S
]
−1
2
(18)
ε S −1
Para S<1, muito comum na prática, a equação (19) apresenta um bom resultado
aproximado.
rpp max ≅ 0,25S p / S < 1
ε d .S −1
ε S −1
a<alim → condução contínua.
alim =
.4
(20)
cuja solução gráfica é apresentada na Figura 5. A região hachurada é a região de operação no modo de condução contínuo. Este
gráfico apresentado por Dewan [2] será utilizado para análise dos demais choppers e,
portanto, reapresentado com mais detalhe
na Figura 8.
VH = +VS
(19)
I a2
rpp
1.0
S=10
I a1 = 0
S=5
VL = 0
1
s=0
0.5
a
continuo
S=2
S
limite
0
0
S=1
d
0
0
0.2
0.4
0.6
0.8
d
1
Figura 5- Limite de operação no modo de
condução contínuo do chopper classe A.
1.0
A equação (20) será reapresentada conforme (21).
rpp
1.0
A=
ε D.S −1
= f (S .D )
ε S −1
(21)
IV-CHOPPER CLASSE B (QII)
0.5
d=0.5
Este chopper, apresentado na Figura 2(b),
opera apenas no II quadrante pois Ea > 0 e
Ia<0 e a MCC opera como gerador, no modo
frenagem regenerativa, uma vez que a energia é devolvida à fonte de alimentação VS.
S
0
0
2
4
6
8
10
Figura 4- Ripple de corrente.
O limite de operação no modo de condução contínuo é obtido de (15) fazendo
Xa1=0
EFEI-IEE/DON
Durante a condução do tiristor Q2, no intervalo tL, o chopper pode ser representado
pelo circuito equivalente 3(b) e durante o
bloqueio de Q2, no intervalo tL, pelo circuito
equivalente 3(a). Como o comportamento do
circuito é semelhante ao do chopper classe
Equações normalizadas para análise de choppers
A, a ondulação de corrente é determinada
igualmente pela (18) ou (19).
A corrente fornecida pelo chopper é negativa e o ciclo de trabalho do chopper não coincide com o ciclo de trabalho do tiristor. O
limite de operação no modo de condução
contínuo é determinado através da (16) com
Xa2 = 0 obtendo-se a equação (22) cuja solução gráfica é apresentada na Figura 6.
alim =
1− ε
− d .s
(22)
1−ε −S
a > alim → condução contínua
(
d = 1 − dq2
V-CHOPPER CLASSE C (QI-II)
O chopper apresentado na Figura 2(c)
opera nos quadrantes I e II. Dependendo de
como os tiristores são disparados este chopper pode operar em 3 modos:
C1 - Q2 bloqueado (dq2 = 0) e Q1 chaveado
(0 < dq1 < 1); d=dq1.
Neste modo de operação o chopper opera
exatamente como o chopper classe A.
C2 - Q1 bloqueado (dq1 = 0) e Q2 chaveado
(0 < dq2 < 1); d=(1-dq2).
)
(23)
Neste modo de operação o chopper opera
exatamente como o chopper classe B.
C3 - Q1 e Q2 disparados e bloqueados alternadamente dq2 = 1-dq1; d=dq1.
VH = +VS
Neste modo de operação o chopper opera
sempre no modo de condução contínuo. A
passagem do modo “tração” para o modo
“frenagem regenerativa” é muito rápida porém é um conversor caro por utilizar duas
chaves eletrônicas de potência.
VL = 0
I a2 = 0
.5
I a1
1
VI-CHOPPER CLASSE D (QI-IV)
a
0
d
O chopper apresentado na Figura 2(d)
opera no I e IV quadrante uma vez que a
corrente é unidirecional, sempre positiva.
1
Figura 6- Limite de operação no modo de
condução contínua no chopper classe B.
Para utilizarmos o gráfico da Figura 8 são
necessárias duas mudanças de coordenadas (24) e (25). Substituindo (24) e (25) em
(22) obtemos novamente (21) que por sua
vez é representada pelo gráfico da Figura 8.
A= (1−a )
(24)
D =1−d =d q 2
(25)
EFEI-IEE/DON
Dependendo de como os tiristores são
disparados e bloqueados este chopper apresenta 6 modos de operação. Nesta configuração faremos as duas considerações
possíveis Ea>0 e Ea<0 não mencionados
nos choppers anteriores.
Ea > 0
D1 - Q1 sempre conduzindo (dq1 = 1) e Q4
chaveado (0<dq4<1). d=dq4.
Neste modo de disparo o chopper opera
exatamente como o chopper classe A. Durante a condução simultânea de Q1 e Q4 o
chopper pode ser representado pelo circuito
equivalente 3(a). Ao bloquearmos apenas
Equações normalizadas para análise de choppers
.6
uma chave, Q4, a livre circulação de corrente, free-wheeling, é feita através de Q1 e D4;
quando o chopper pode ser representado
pelo circuito equivalente 3(b). Portanto, no
intervalo tH Va=+VS e no intervalo tL, Va=0,
como no chopper classe A.
O limite de operação no modo de condução contínuo é determinado pela (34) obtido
de (30) com Xa1=0.
A freqüência de operação do chopper é
igual à freqüência de chaveamento de Q4,
não aproveitando uma virtude desta configuração mostrada no modo D3.
a<alim → condução contínua
D2 - Q1 e Q4 disparados e bloqueados simultaneamente d=dq1=dq4, 0<d<1
a Lim =2
ε d .S −1
−1
ε S −1
(34)
Para utilizarmos a equação (21) ou o gráfico da Figura 8, é necessário a mudança de
coordenada (36).
alim = 2. f (S.D )−1
(35)
Durante a condução simultânea dos tiristores, no intervalo tH, o chopper pode ser representado pelo circuito equivalente 3 (a).
A=
xa (t )=(1−a)−[(1−a) − X a1 ]ε −t / T
D3 - Q1 e Q4 chaveado com defasamento
de 180o; dq1=dq4=dq; 0,5<dq<1
(26)
No instante t=tL,
X a 2 =(1−a )−(1−a − X a1 )ε − d .S
(27)
Durante o bloqueio simultâneo dos tiristores, a corrente é forçada a circular através
dos dois diodos resultando no circuito equivalente da Figura 3(c) onde I(∞)=-(1+a)
xa (t ' ) = −(1 + a) − [−(1 + a) − X a2 ]ε
X a1 = − (1 + a ) + (1 + a + X a 2 )ε
− S (1− d )
−t '/ Ta
(28)
(29)
Resolvendo (27) e (29) obtemos (30) e
(31):
X a1 = 2
d .S
ε −1
− a −1
ε S −1
X a2 =2
1−ε − d .S
1− ε −.S
− a −1
(30)
(31)
1− ε − dS
ε dS − 1 
r pp = 2 
−

−S
ε S − 1
 1−ε
(32)
rpp ≅ 0,5S p / S < 1
(33)
(a +1)
(36)
2
Durante a condução simultânea dos dois
tiristores, no intervalo tH, temos o circuito
equivalente 3(a). Durante o bloqueio de um
tiristor, intervalo tL, o outro tiristor e um diodo
conduzem obtendo o circuito equivalente da
3(b). O comportamento deste chopper é semelhante ao chopper classe A, porém a freqüência de operação do chopper é o dobro
da freqüência de chaveamento dos tiristores,
ou seja T=Tq/2.
Com este artifício conseguimos reduzir a
ondulação de corrente sem aumentarmos a
freqüência de chaveamento das chaves eletrônicas que provocaria aumento nas perdas
por chaveamento.
S=
Tq
(38)
2.Ta
d = 2.d q −1
`
(39)
Ea<0
D4 - Q1 bloqueado (dq1=0) e Q4 chaveado
(0<dq4<1)
Durante a condução Q4 no intervalo tH a
tensão de saída é zero conforme o circuito
EFEI-IEE/DON
Equações normalizadas para análise de choppers
equivalente 3(b). Xa(tH)=Xa2 Lembrando que
“a” é negativo.
xa (t ) = −a − (− a − X a1 )ε −t / Ta
(40)
X a 2 = − a − (− a − X a1 )ε − d .S
(41)
.7
Observe que a tensão de saída é negativa
o que significa inversão no sentido de rotação do motor.
+Vs
D1
+Vs
Durante o bloqueio de Q4 no intervalo tL a
tensão de saída é -Vs devido à condução de
D1 e D4 conforme o circuito equivalente
3(c). Xa(tL)=Xa1
xa (t ' ) = −(1 + a) + (1 + a + X a 2 )ε −t '/ T
(42)
X a1 = −(1 + a) + (1 + a + X a 2 )ε − S (1−d )
(43)
Resolvendo (41) e (43) obtemos (44) e
(45)
ε d .S −1
− a−1
X a1 = S
ε −1
1− ε −dS
X a2 =
−a−1
1−ε −S
1−ε −dS ε d S −1
r pp =
− S
1− ε −S
ε −1
(44)
D2
D5
-Vs
D4
-Vs
Q1
Q4
+Vs
D3
Q1
(45)
Q4
D6
-Vs
(46)
0
1
rppmax ≅ 0,25.S p / S < 1
(47)
D1 D3
D4 D6
a
O limite de operação no modo de condução contínuo é determinado por (48) obtido
de (44) para Xa1=0. A solução gráfica de
(48) é apresentada na Figura 7.
a
0
-1
0
d
1
d
1
0
d
1
1
D2 D5
d .S
ε −1
−1
(48)
ε S −1
a<alim ou a>alim→condução contínua
alim =
Para utilizarmos o gráfico da Figura 8 é
necessário a mudança de coordenada (49).
A = (a+1)
EFEI-IEE/DON
(49)
a
-1
0
Figura 7- Chopper classe D. Limite de operação no modo de condução contínuo
e formas de onda.
D5 - Q1 e Q4 chaveados simultaneamente.
dq1=dq4=dq=d; 0<d<1.
Equações normalizadas para análise de choppers
A ondulação e o limite de operação no
modo de condução contínuo são determinados exatamente como no chopper D2, lembrando apenas que a<0. Neste modo de operação o chopper fornece potência à MCC
operando como gerador no modo de operação conhecido como “plug in”, um recurso
para manter corrente, e consequentemente
o conjugado frenante, em altos valores nas
baixas rotações.
D6 - Q1 e Q4 chaveamento com defasamento de 180o dq1=dq4=dq; 0<dq<0,5
Neste modo de operação o comportamento do chopper é semelhante ao chopper D4,
porém, a freqüência de operação do chopper é dobro da freqüência de chaveamento
dos tiristores. Um recurso interessante para
obter baixos valores de ondulação.
T=
S=
O limite de operação no modo de condução contínuo das cinco configurações de
chopper pode ser determinado pela equação
(20) ou pelo gráfico da Figura 8, bastando
uma simples mudança de coordenadas.
A ondulação pico a pico pode ser determinada através da equação (17) no caso de
tensão de saída unipolar Va=(+Vs,0) ou (0,Vs) ou pela equação (32) no caso de tensão
bipolar Va=(+Vs,-Vs).
1
S=0
1
(50)
2
2
5
Tq
10
(51)
2.Ta
d = 2.d q
(52)
VII-CHOPPER CLASSE E (QI-II-III-IV)
Este chopper de quatro quadrantes pode
operar em qualquer um dos modos anteriores; pode operar em apenas um quadrante
(I, II, III ou IV), em dois quadrantes regenerativo (I-II ou III-IV), em dois quadrantes com
velocidade bidirecional (I-IV ou II-III), nos
quatro quadrantes (aceleração, frenagem
regenerativa e inversão) e também como inversor monofásico.
VIII - CONCLUSÃO
Qualquer chopper, nos vários modos de
operação, pode ser representado por um
dos três circuitos equivalentes da Figura 3
que por sua vez pode ser equacionado através de uma única equação normalizada (9).
A equação exata para cada intervalo é obtida pela definição do valor final X(∞)=(1-a), -a
EFEI-IEE/DON
ou -(1+a) e pelo valor inicial X(o)=Xa1 ou
Xa2.
A
Tq
.8
0
0
D
1
Figura 8- Gráfico para determinação do
limite de operação no modo de condução
contínuo.
REFERÊNCIAS:
[1] W. Moto Jr- "Introduction to Power Eletronics" Westinghouse, 1977.
[2] S. B. Dewan and A. Straughen- “Power
Semiconductor Circuits"; Wiley, 1975.
[3] S. B. Dewan, G. R. Slemon and A. Straughen- "Power Semiconductor Drives",
Wiley, 1984.
[4] P. C. Sen- "Thyristor D. C. Drives", Wiley,
1981.
Artigo apresentado no II SEMINÁRIO DE
ELETRÔNICA DE POTÊNCIA, SEP-89,
pp. 215-220. Florianópolis, 11-15 de Dezembro de 1989.