ESTRUTURA DO GRUPO SU(2)

ESTRUTURA DO GRUPO SU(2) EM SISTEMAS DISCRETOS.
Alexandre Drinko (PIBIC/Fundação Araucária/UEPG), Antonio Sérgio Magalhães de
Castro (Orientador), e-mail: [email protected].
Universidade Estadual de Ponta Grossa/Departamento Física.
1.05.00.00-6 / 1.05.01.02-9 Física / Física Clássica e Física Quântica; Mecânica
e Campos
Palavras-chave: Simetria SU(2), spin 1/2, sistema discreto.
Resumo:
Faz-se um breve estudo sobre simetrias, com destaque na estrutura do
grupo SU(2). Consideramos sua aplicação na descrição da dinâmica de spin 1/2
interagindo com um campo magnético, com ênfase na técnica de Ressonância
Magnética nuclear (RMN). Apresenta-se uma análise desta dinâmica por meio do
vetor de Bloch, representando a precessão do spin em torno de um dado eixo.
Introdução
Tanto na Física Clássica quanto na Quântica, simetrias estão associadas ao
conceito de grupo e álgebra de Lie (ARFKEN, WEBER, 2007). Define-se um grupo
abstrato como um conjunto de elementos, munido de uma operação de fechamento
com a existência do elemento identidade e elementos inversos correspondentes a
cada elemento do Grupo. O conceito de álgebra de Lie está associado à existência
de um espaço vetorial tangente ao grupo de Lie (grupo topológico) na identidade.
Os geradores da álgebra de Lie são elementos de um espaço vetorial complexo.
Neste trabalho revisamos o grupo unitário SU(2), associado a rotações em
um espaço de Hilbert bidimensional da Mecânica Quântica (SAKURAI,
NAPOLITANO. 2013). A simetria pode ser detectada na Mecânica Quântica
analisando a estrutura do operador Hamiltoniano ̂ Conhecendo a forma do
operador Hamiltoniano, é possível detectar sua correspondente simetria e também
construir o operador de evolução temporal que descreve a dinâmica do estado
quântico de acordo com a simetria dinâmica do Hamiltoniano.
Revisão de literatura
Com base no estudo de simetrias, compreendidas como um conceito
fundamental da Física analisa-se como um grupo pode estar associado à evolução
temporal de um sistema quântico discreto a partir da simetria expressa pelo
Hamiltoniano.
De início, verificou-se a utilização do conceito de simetria e suas implicações
na Mecânica Clássica, depois, analisar sua manifestação na Mecânica Quântica
seguindo o desenvolvimento elaborado por Cius (CIUS, De CASTRO, 2016).
Assim, o objetivo central deste trabalho é compreender o conceito de grupo
e suas aplicações em sistemas quânticos discretos nos quais os seus operadores
Hamiltonianos podem ser escritos em termo dos elementos da álgebra SU(2). Além
disso, explorar a sua relação com o operador de evolução temporal.
Resultados e Discussão
A compreensão da simetria para sistemas clássicos tem como ponto de
partida a análise da invariância de determinados parâmetros ou quantidades, tendo
implicação na redução de graus de liberdade de um sistema, permitindo uma
simplificação na análise da sua evolução dinâmica. Pode-se explorar as simetrias
na Mecânica Clássica através do Lagrangiano do sistema físico em questão e,
consequentemente do correspondente Hamiltoniano (MARTINS, 1999).
Ideia similar pode ser estendida para sistemas quânticos, onde o foco
principal consiste na análise da invariância de quantidades mensuráveis,
representadas por operadores definidos no espaço de Hilbert e não mais por
funções escalares dependentes de variáveis clássicas. O elemento central para o
estudo das simetrias dinâmicas de sistemas quânticos consiste em estudar a forma
do operador Hamiltoniano e os invariantes associados, tema a ser considerado em
mais detalhes em estudos futuros. Neste trabalho o interesse está em analisar
como a simetria dinâmica SU(2) se manifesta por meio da forma do operador
Hamiltoniano e considerar a análise de um exemplo prático.
Enquanto em sistemas clássicos, rotações no espaço físico são expressas
pelo grupo SO(3,R), no espaço de Hilbert da mecânica quântica tem-se o grupo
SU(2) como o seu análogo (isomorfo), responsável por rotações dos vetores de
estados do sistema quânticos isolados (ARFKEN, WEBER, 2007). O grupo SU(2) é
um grupo de matrizes unitárias de ordem 2 e determinante 1, cuja parametrização
está definida em termos dos parâmetros complexos
e
, de acordo com
(
)
e os geradores da correspondente álgebra são representados pelas matrizes de
Pauli. Já os elementos do grupo SU(2) podem ser escritos na forma (3), onde ,
,e
são números reais.
(
)
(
)
(
)
Na descrição da dinâmica quântica, a evolução temporal do estado de um
sistema quântico é descrita pela equação de Schrödinger
⟩
̂
⟩
⟩ representa o estado do sistema físico e ̂
onde o vetor
é o operador
Hamiltoniano do sistema, gerador de translação temporal do sistema. A solução
desta equação fornece a evolução do estado inicial em um instante de tempo inicial
, a um estado final em um instante de tempo qualquer. Logo, o estado inicial e
final do sistema estão relacionados através de um operador de evolução temporal
̂
de acordo com a equação
̂
⟩
⟩
Pode-se explorar um problema de interesse prático em RMN com simetria
dinâmica SU(2), que consiste na dinâmica de um spin 1/2 interagindo com um
campo magnético sobre um referencial fixo, por exemplo. O Hamiltoniano de
interção entre o spin e o campo magnético ⃗
pode ser escrito em termos de
elementos da álgebra do SU(2), cuja forma se expressa por
̂
⃗
̂
onde
e é a razão giromagnética do núcleo e
sendo a frequência
de Larmor (frequência de precessão do spin em torno do eixo). Os dois
autoestados de ̂ correspondem às energias
para spin down ⟩
e
para spin up ⟩
. O operador de evolução temporal escrito na forma
dos elementos SU(2),
̂
̂
(
)
̂
aplicando o operador de evolução temporal (7) a um estado inicial na forma
⟩
⟩
⟩, onde é o ângulo entre o vetor de estado e o eixo
e o ângulo azimutal, observa-se a evolução do estado inicial para o estado final:
⟩
(
⟩
)(
⟩)
⟩ precessiona em torno do eixo com um ângulo
Desta forma o estado
fixo e frequência angular
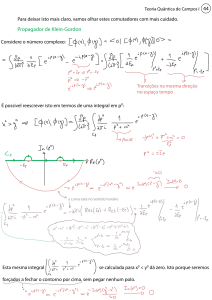
. Para visualizar este comportamento do vetor de
estado, utiliza-se da representação da esfera de Bloch (NIELSEN; CHUANG,
2010). Escrevendo a matriz densidade em termos das matrizes de Pauli
⟩⟨
Sendo
o
vetor
,
(verde) e
e tempo
(azul).
de
Bloch,
que
para
este sistema é na forma
, ilustrado na Figura 1, com
, para os casos em que
(vermelho),
Figura 1 - Evolução do vetor de Bloch para um referencial fixo. (Fonte: CIUS.D; DE CASTRO.A.S.M,
2016)
Conclusões
No seu aspecto mais simples, o conceito de simetria em sistemas físicos
clássicos, está associado a transformações de coordenadas e seus respectivos
invariantes ou quantidades conservadas. Tais transformações podem ser definidas
por meio de translação temporal, espacial e rotação. Este aspecto é importante
para entender o papel do estudo da simetria em física.
No caso de um sistema quântico, conhecendo a álgebra associada ao
operador Hamiltoniano é possível saber a forma do operador de evolução temporal,
pois ele é um elemento do grupo associado. As propriedades de simetria
pertinentes a um dado operador Hamiltoniano estão relacionadas à parametrização
do operador de evolução temporal. Tem-se neste aspecto uma motivação para o
estudo das propriedades gerais das simetrias e grupos, devido a muitos grupos de
Lie serem conhecidos e suas parametrizações estão definidas a priori. Para casos
mais gerais onde o Hamiltoniano depende do tempo, encontrar solução analítica
para os parâmetros dos elementos do operador de evolução temporal nem sempre
é possível, mesmo que ele tenha uma dada simetria. No entanto, o fato de possuir
uma simetria, implica na possibilidade de construir métodos analíticos, permitindo
classificar sistemas analiticamente solúveis com simetria definida, similares ao
método de Messina-Nakazato (MESSINA,NAKAZATO,2014), para sistemas de Nníveis com simetria SU(2) aplicável a sistemas de spins por meio de RNM.
Agradecimentos
Ao PIBIC/FUNDAÇÃO ARAUCÁRIA pelo apoio financeiro. Ao Prof. Dr.
Ruben Auccaise e Danilo Cius pelas valiosas discussões sob os temas
desenvolvidos.
Referências
ARFKEN e WEBER, Física Matemática: Métodos Matemáticos para Engenharia e
Física. Rio de Janeiro: Elsevier, 2007.
CIUS. D; DE CASTRO.A.S.M, Estudo de Sistemas Quânticos Discretos com
Simetria SU(2), Ponta Grossa, DEFIS-UEPG, 5 de Abril de 2016.
GOLDSTEIN. H, POOLE. C, SAFKO. J, Classical Mechanics, 3ªed, 2000.
GROSS. D. J, The role of symmetry in fundamental physics, Vol.93, p.14256-14259,
December, 1996.
MARTINS. A. S, Simetrias e leis de conservação na Mecânica Clássica, Revista
Brasileira de Ensino de Física, Vol.21, nº1, pág 33-39, Março 1999.
MESSINA. A; NAKAZATO. H, Analytically solvable Hamiltonians for quantum twolevel systems and their dynamics. Journal of Physics A: Mathematical and
Theoretical Vol.47, 445302, 2014.
NIELSEN. M. A; CHUANG. I. L, Quantum Computation and Quantum Information,
Cambridge, 2010.
ROSEN. J, Fundamental Manifestations of Symmetry in Physics, Foundations of
Physics, Vol. 20, Nº3, pág 283-307, 1990.
SAKURAI, J. J., NAPOLITANO, J. Mecânica quântica moderna. 2. ed. Porto Alegre:
Bookman, 2013.