O MMC e o MDC

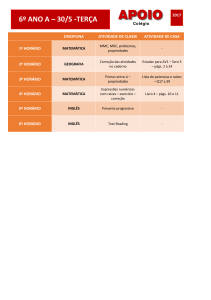
O MMC e o MDC
A matemática tem se mostrado cada vez mais uma ferramenta importante e necessária em nosso
cotidiano, mas por algumas razões as pessoas têm dificuldade de associar o conteúdo com um
problema proposto. Entre estas dificuldades, pode-se destacar a aplicação do Mínimo Múltiplo
Comum (MMC) e do Máximo Divisor Comum (MDC).
Vamos ver, separadamente, o que significa e aonde se aplica cada um destes termos.
1. MMC (Mínimo Múltiplo Comum) e suas aplicações:
Para entendermos o que é MMC, primeiramente vamos estudar como se obtém o múltiplo de um
número.
Para obtermos o múltiplo de um número qualquer, basta realizarmos a multiplicação
desse número por qualquer número natural.
Exemplo:
Múltiplos de 12:
{0, 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132,...}
Múltiplos de 16:
{0, 16, 32, 48, 64, 80, 96, 112, 128,...}
Ao analisar os múltiplos de 12 e 16, podemos dizer que o MMC entre eles é o 48, pois com
exceção do zero, o MENOR valor que é múltiplo entre 12 e 16 ao mesmo tempo é o 48.
Mas como extrair o MMC sem precisar encontrar os múltiplos de cada um dos valores
separadamente? Basta efetuar a fatoração simultânea. Veja:
Fatorar é dividir um número em fatores primos e em ordem crescente, ou seja, começando
sempre pelo menor fator possível.
Mas como a maior dificuldade é encontrar em quais situações se aplicam o MMC, geralmente o
utilizamos em problemas que precisamos saber de quanto em quanto tempo dois veículos se
encontrarão, ou seja, de quanto em quanto tempo ocorrerá um evento.
Exemplo:
Três automóveis disputam uma corrida em uma pista circular. O mais rápido dá uma volta em 2
minutos, o outro completa a volta em 2 minutos e meio, e o mais lento completa a volta em 3
minutos. No fim de quanto tempo os três automóveis voltarão a se encontrar no início da pista se
todos partiram exatamente no mesmo instante? E quantas voltas cada um terá dado após se
reencontrarem?
Bem, como nem todos os valores são inteiros (2 minutos e meio), e estão em minutos, para
facilitar os cálculos é interessante transformá-los em segundos:
2 minutos = 120 segundos
2,5 minutos = 120 + 30 = 150 segundos
3 minutos = 180 segundos
Encontraremos agora o MMC entre 120, 150 e 180 segundos.
Isto significa que os três automóveis voltarão a se encontrar ao mesmo tempo no início da pista
após 1800 segundos, ou seja, 30 minutos após o início da corrida.
Agora para saber quantas voltas cada carro terá dado na pista ao se reencontrarem, basta dividir
o MMC encontrado pelo tempo gasto por cada para completar uma volta:
1800 : 120 = 15 voltas
1800 : 150 = 12 voltas
1800 : 180 = 10 voltas
Tendo isto bem fixado em mente, qualquer outra pergunta que for feita é possível responder com
facilidade.
2. MDC (Máximo Divisor Comum) e suas aplicações:
Da mesma forma que foi feito com o MMC, faremos com o MDC.
Obter o divisor de um número é obter todos os valores inteiros pelos quais este número pode ser
dividido.
Exemplo:
Divisores de 12:
{1, 2, 3, 4, 6, 12}
Divisores de 16:
{1, 2, 4, 8, 16}
Ao analisar os divisores de 12 e 16, pode-se dizer que o MDC entre eles é o 4, pois é o MAIOR
valor que divide 12 e 16 ao mesmo tempo.
É possível também extrair o MDC entre dois ou mais números através da fatoração simultânea.
Veja:
Porém, os fatores que utilizaremos para encontrar o MDC entre eles serão apenas aqueles que
os dividem ao mesmo tempo. Observe que a partir do terceiro fator apenas um dos números era
dividido. Logo MDC (12, 16) = 4.
Geralmente, o MDC é aplicado em problemas que precisamos encontrar o maior pedaço possível,
ou a quantidade máxima de componentes de cada grupo. São problemas que envolvem termos
como “quantidade máxima” ou “maior possível”.
Exemplo:
Uma pessoa comprou para decorar sua festa 120 bombons de coco, 180 do tipo trufas e 200
bombons de cereja. Quantos bombons de cada sabor deverão ser colocados em cada caixa
decorada, sabendo que essas quantidades deverão ser as maiores possíveis?
O primeiro passo é encontrar o MDC entre 120, 180 e 200, que representará a quantidade de
caixas a serem decoradas, de forma que as quantidades sejam valores inteiros e os maiores
possíveis.
Isso significa que serão decoradas 20 caixas. Logo a quantidade de bombom de cada sabor
dentro da caixa será:
Bombom de coco: 120 : 20 = 6 bombons
Trufas: 180 : 20 = 9 trufas
Bombom de cereja: 200 : 20 = 10 bombons
Ou seja, em cada caixa haverá 6 bombons de coco, 9 trufas e 10 bombons de cereja.
Entendendo este processo, qualquer outra pregunta feita é possível ser respondida facilmente.
3. Algumas observações sobre o MMC:
1) O MMC entre dois ou mais números primos é sempre a multiplicação entre eles;
2) Se A é múltiplo de B, o MMC entre A e B é igual a A;
3) Se multiplicarmos dois ou mais números por um número natural não nulo, o MMC também
ficará multiplicado por este número natural.
4. Algumas observações sobre o MDC:
1) O MDC entre dois ou mais números primos vale 1;
2) Se A é múltiplo de B, o MDC entre A e B é igual a B;
3) Se multiplicarmos dois ou mais números por um número natural maior que zero, o MDC
entre eles também ficará multiplicado por esse número;
4) Quando o MDC entre dois números, não necessariamente primos, for 1 eles são chamados
de primos entre si.