introdução ao mhs - Prof. Frederico Mercadante

MINISTÉRIO DA EDUCAÇÃO
SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE GOIÁS
Campus Itumbiara
Docente: Prof. Frederico Mercadante
Aluno(a):_____________________________________________________________________ Técnicos Integrados
Itumbiara, ____ de março de 2013
Duração: 1h 30min
FÍSICA III
ATIVIDADE SOBRE M.H.S. – INTRODUÇÃO
INSTRUÇÕES
1ª. A cada dois erros ortográficos será descontado um (01) ponto;
2ª. Faça letra legível e com capricho para garantir a correção;
3ª. Use somente caneta de tinta azul ou preta. Prova respondida a lápis ou rasurada perderá o direito de reclamações posteriores;
4ª. Se ocorrer falha ao escrever, passe um traço sobre a palavra errada. NÃO UTILIZE PARÊNTESES NEM CORRETIVO;
5ª. Sua resposta deve ser completa, clara; caso contrário, perderá na pontuação;
6ª. Seu texto deverá ser registrado de acordo com a norma padrão da língua portuguesa;
7ª. Evite empregar em sua resposta palavras ou expressões que funcionem como "gancho" atado à pergunta. Textos iniciados com PORQUE, ISTO É, POIS,
QUE, entre outros conectivos, cometem falhas neste aspecto;
8ª. Não empregue abreviações, a não ser que esteja se referindo a uma sigla. Não repita em demasia a mesma palavra;
9ª. Quando opinar, evite expressões como: “eu acho que”, “eu penso que”. FUNDAMENTE SUAS RESPOSTAS COM ARGUMENTOS VÁLIDOS;
10ª. Se a pergunta implicar em respostas do tipo SIM ou NÃO, procure elaborar sentenças integrando esses advérbios dentro da frase;
11ª. Escrever ETC. ou E OUTROS pode ser compreendido como falta de argumentação.
Caros companheiros, esta atividade tem por finalidade verificar/aperfeiçoar seus conhecimentos sobre os conceitos
iniciais sobre M.H.S., bem como suas aplicações corriqueiras.
Faça-a com calma e muita atenção lembrando que cada uma das questões deverá ser justificada conforme o estudado
em sala de aula sob a orientação de seu professor na folha pautada que você recebeu em anexo sendo que as questões
deverão ser claramente identificadas.
Esta atividade deverá ser desenvolvida em equipes de duas pessoas ou individualmente sendo que cada integrante da
equipe entregará sua folha de resposta impreterivelmente no próximo encontro de Física (assim que adentrar em sala).
QUESTÕES
TEÓRICAS
Questão 00 – Defina o que é movimento oscilatório/vibratório e o que é movimento periódico. Cite exemplos de cada caso.
Questão 01 – Diga, com suas palavras, o que você entende por um oscilador harmônico simples (M.H.S.)?
Questão 02 – O que é amplitude, período e frequência em um M.H.S.? Faça um esquema ilustrativo.
Questão 03 – Que relação matemática há entre período e frequência?
Questão 04 – Descreva o que é um pêndulo simples e determine a equação para seu cálculo.
Questão 05 – Descreva o que é um pêndulo cônico e determine a equação para seu cálculo.
Questão 06 – Descreva o que é um sistema massa-mola, como ele funciona e determine a equação para seu cálculo?
Questão 07 – O que ocorrerá com o período de oscilação de um pêndulo simples se quadriplicar seu comprimento?
Questão 08 – O que ocorrerá com o período de um sistema massa mola se sua amplitude ficar reduzida em 16 vezes?
Questão 09 – O que é um sismógrafo? Para que ele serve?
Questão 10 – Um corpo executa um movimento harmônico simples, preso à extremidade de uma mola. Diga se o tempo gasto
pelo corpo para efetuar uma vibração completa aumentará, diminuirá ou não sofrerá alteração, em cada um dos
seguintes casos:
a) o corpo é substituído por outro de massa maior;
b) a mola é substituída por outra mais macia;
c) o corpo é colocado a oscilar com uma amplitude menor.
Questão 11 – Suponha que um astronauta levasse um relógio de pêndulo para a Lua nas mesmas condições de temperatura.
a) O período aumentaria ou diminuiria?
b) E a frequência do pêndulo?
c) Então o relógio se adiantaria ou se atrasaria?
d) Para acertar o relógio, o astronauta deveria aumentar ou diminuir o comprimento do pêndulo?
Questão 12 – Sabendo-se que um pêndulo simples tem comprimento de 1,00 metro e possui período de 2,00 segundos. Determine
o valor da aceleração gravitacional local. Considere que o único campo que influencia esse movimento seja o
gravitacional.
Questão 13 – Proponha uma maneira de se determinar a aceleração gravitacional média de um local através de um pêndulo
cônico.
PROBLEMAS – TESTES
Questão 01 – Uma garota decide brincar em um balanço
suspenso por uma corda de comprimento L. Ela parte da
posição em que a corda faz um ângulo de 60o com a
vertical, como mostra a figura abaixo, com velocidade
inicial nula.
Dados: cos 60o = 1/2; sen 60o = 3 / 2
segundo uma trajetória retilínea, em torno de uma
posição de equilíbrio (posição 0), isto é, entre os pontos
A e B. A energia cinética máxima atingida é 0,1 J.
Julgue os itens abaixo:
m
A
I.
II.
III.
IV.
V.
a)
Deduza uma expressão que permita calcular a
velocidade com que a garota passa pela posição B
(posição mais baixa), em função de g e de L.
b) Sendo 60kg a massa da garota, 2,5m o
comprimento da corda e 900 newtons a máxima
tensão suportável pela corda, determine a
velocidade que terá no ponto C (30o com a
vertical), caso chegue a este ponto. Adote g = 10
m/s2..
Questão 02 – Deseja-se determinar a aceleração da
gravidade em Goiânia. Para isto dispõe-se de: fita
métrica, balança, cronômetro, transferidor e um pêndulo
simples, que é um sistema constituído por uma partícula
de massa m, suspensa por um fio ideal. Sabendo-se que
o período de um pêndulo simples é dado por 2π L / g ,
descreva, resumidamente, um procedimento para
determinar esta aceleração.
Questão 03 – Um pêndulo é constituído por uma casca
esférica muito fina de metal, cheia de água. Na parte
inferior da esfera existe um furo de modo tal que a água
vai saindo enquanto o pêndulo oscila.
Com relação ao período deste pêndulo pode-se afirmar
que:
a) Não se altera porque o período do pêndulo
independe da massa.
b) Diminui até um certo valor porque está perdendo
massa.
c) Diminui até um certo valor e depois aumenta
novamente voltando ao período inicial.
d) Aumenta até um certo valor e depois diminui
voltando ao período inicial.
e) Aumenta até um certo valor porque está perdendo
massa.
0
B
A energia mecânica do corpo no ponto 0 é 0,1 J.
O período do movimento é 0,4 s.
A energia potencial elástica no ponto A é 0,1 J.
A amplitude do movimento é 0,2 m.
A energia mecânica do corpo nos pontos a e B é
exclusivamente cinética.
São corretas:
a) I, II e III
b) I, III e V
c) I, III e IV
d) I, II, IV e V
e) I, II, III, IV e V
Gab: C
Questão 05 – SOBE, DESCE, SOBE, DESCE, SOBE,
DESCE, SOBE, DESCE...
Seja uma partícula em Movimento Harmônico Simples
regido pela função: x = 0,1 cos (2πt) para x em metros e
t em segundos. Responda:
a) O que representam as constantes 0,1 e 2π?
b) Qual a freqüência, em hertz, do movimento?
c) Em que posição se encontra a partícula em t = 0s?
Qual a velocidade neste instante?
d) Em que posição a energia cinética é máxima? Em
que instante isto acontece?
Gab:
a)
b)
c)
d)
0,1 representa a amplitude do movimento (em metros); 2 π
representa a freqüência angular (em radianos por segundos)
1Hz
0,1m; 0 m/s
em x = 0; isto ocorre nos instantes 1,3,5,7......
Questão 06 – Quando um pêndulo simples de massa 2,0 kg
e comprimento 0,5 m oscila, a energia cinética nos
pontos mais altos da trajetória é:
a) -1,0 J
b) 0,0 J
c) 0,25 J
d) 1,0 J
e) 2,0 J
Gab: D
Gab: B
Questão 04 – A figura mostra um sistema ideal massa-mola,
apoiado sobre uma superfície horizontal sem atrito. O
corpo de massa m = 0,2kg está preso à mola de
constante elástica k = 5N/m e oscila horizontalmente,
Questão 07 – Um pêndulo simples oscila, num local onde a
aceleração da gravidade é 10m/s², com um período de
oscilação igual a pi/2 segundos. O comprimento deste
pêndulo, em metros é:
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 2 de 11
a)
b)
c)
d)
e)
x(m)
1,6
0,16
62,5
6,25
0,625
2
Gab: E
0
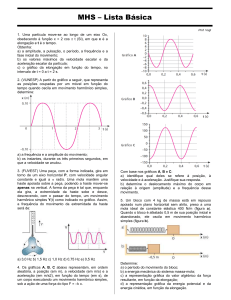
Questão 08 – Um bloco oscila harmonicamente, livre da
resistência do ar, com uma certa amplitude, como
ilustrado na figura abaixo.
1
2
3
t(s)
4
-2
A equação da posição em função do tempo para este
movimento harmônico é dada por x = A cos(ωt
+
φ). A partir do gráfico, encontre as constantes A, ω e φ
.
Gab:
A = 2m
Ao aumentar sua amplitude de oscilação, pode-se
afirmar que:
a) a constante elástica da mola não se altera,
aumentando o período e a velocidade máxima do
oscilador.
b) o período aumenta, a velocidade máxima diminui e
a constante elástica da mola não se altera.
c) o período, a velocidade máxima do oscilador e a
constante elástica da mola aumentam.
d) o período e a constante elástica da mola não se
alteram, aumentando apenas a velocidade máxima
do oscilador.
e) o período, a velocidade máxima do oscilador e a
constante elástica da mola não se alteram.
π
rad / s
2
φ = π/2
ω=
Questão 11 – O gráfico representa a elongação de um corpo
em movimento harmônico simples (MHS) em função
do tempo. A amplitude, o período e a freqüência para
este movimento são dados, respectivamente, por:
0
Gab: D
-5
Questão 09 – Um pêndulo, constituído por um fio ideal e
uma esfera de peso P, oscila entre duas posições
extremas A e B, conforme ilustra a figura acima. Nessas
extremidades, a relação correta entre os módulos do
peso e da tração (T) no fio é:
.
X(m)
5
a)
b)
c)
d)
e)
2
.
. .
4
6
8
t(s)
10m, 4s, 1/8Hz
5m, 4s, 1/4Hz
10m, 8s, 1/4Hz
5m, 8s, 4/9Hz
0, 8s, 1/8Hz
Gab: D
α α
A
a)
b)
c)
d)
e)
B
P = T.cosα
P = T.tgα
T = P.tgα
T = P.cosα
T = P.senα
Gab: D
Questão 10 – O gráfico abaixo mostra a posição em função
do tempo de uma partícula em movimento harmônico
simples (MHS), no intervalo de tempo entre 0 e 4 s.
Questão 12 – Comenta-se que o célebre físico e matemático
Galileo Galilei, ao observar a oscilação do lampadário
da catedral de Pisa, na Itália, concluiu tratar-se de um
movimento periódico, semelhante ao que hoje
chamaríamos de pêndulo simples. Para tal conclusão,
teria medido o período do movimento, utilizando, como
unidade de medida para o tempo, seu próprio batimento
cardíaco. Se considerarmos um grande pêndulo simples,
de comprimento 10 m, oscilando num local onde g = 10
m/s2, e que a freqüência dos batimentos cardíacos é de
86 batidas por minuto, o período do movimento desse
pêndulo será de aproximadamente:
a) 3 batidas
b) 6 batidas
c) 9 batidas
d) 12 batidas
e) 15 batidas
Gab: C
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 3 de 11
Questão 13 – Um corpo de 50 g, preso à extremidade de
uma mola ideal (constante elástica = 3,2 N/m)
comprimida de 30 cm, é abandonado do repouso da
posição A da figura. A partir desse instante, o corpo
inicia um movimento harmônico simples. Despreze os
atritos e adote o eixo x com origem no ponto de
equilíbrio do corpo (ponto O) e sentido para a direita. A
função que mostra a velocidade desse corpo em função
do tempo, no Sistema Internacional, é:
A
O
B
X
Origem
a)
v = –2,4 sen (8.t + π)
b) v = –0,3 sen (3,2.t +
a)
b)
c)
d)
e)
3,0Hz
1,5Hz
1,0Hz
0,75Hz
0,5Hz
Gab: B
Questão 16 – Um corpo apoiado sobre uma superfície
horizontal lisa e preso a uma mola ideal, comprimida de
20 cm, é abandonado como mostra a figura. Esse corpo
realiza um m.h.s. de freqüência 5 Hz, sendo O o seu
ponto de equilíbrio. A velocidade (v) adquirida pelo
corpo, no SI, varia com o tempo (t) obedecendo à
função:
π
)
2
c) v = –7,2 sen (4.π.t + π)
d) v = –2,7 sen (4.t + π)
e)
v = –1,2 sen (2.t +
π
)
4
Gab: A
Questão 14 – Um corpo realiza um movimento harmônico
simples
(MHS),
conforme
a
equação:
π

X = 6 . cos 12t + 
2

Pode-se afirmar que a velocidade angular do corpo que
realiza esse MHS, é:
a) 6 rad/s
b)
π
rad/s
2
3π rad/s
c)
d) 72 rad/s
e) 12 rad/s
Gab: E
Questão 15 – Uma peça, com a forma indicada, gira em
torno de um eixo horizontal P, com velocidade angular
constante e igual a π rad/s. Uma mola mantém uma
haste apoiada sobre a peça, podendo mover-se apenas
na vertical. A forma da peça é tal que, enquanto ela
gira, a extremidade da haste sobe e desce, descrevendo,
com o passar do tempo, um movimento harmônico
simples Y(t) como indicado no gráfico.
a)
b)
c)
d)
e)
v = -2 senπ (10π .t + π )
v = + 2π cos(10π. t + π)
v = - π sen (10π .t +π /2)
v = + π cos (10π .t + π /2)
v = -2π sen(10π. t + 2π/3)
Gab: A
Questão 17 – Um corpo oscila em torno de um ponto com
M.H.S. de amplitude 30 cm. O valor absoluto da
elongação do movimento do corpo, no instante em que
3
a energia cinética é igual a
da energia mecânica, é:
4
a) 25 cm
b) 20 cm
c) 18 cm
d) 15 cm
e) 12 cm
Gab: D
Questão 18 – Um corpo C, de massa 1,0 . 10–1 kg, está
preso a uma mola helicoidal de massa desprezível e que
obedece à Lei de Hooke. Num determinado instante, o
conjunto se encontra em repouso, conforme ilustra a
figura 1, quando então é abandonado e, sem atrito, o
corpo passa a oscilar periodicamente em torno do ponto
O. No mesmo intervalo de tempo em que esse corpo vai
de A até B, o pêndulo simples ilustrado na figura 2
realiza uma oscilação completa. Sendo g = 10 m/s2, a
constante elástica da mola é:
Assim, a freqüência do movimento da extremidade da
haste será de
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 4 de 11
a)
b)
c)
d)
e)
0,25 N/m
0,50 N/m
1,0 N/m
2,0 N/m
4,0 N/m
Gab: B
Questão 19 – A função horária da posição de uma partícula
que realiza um M.H.S. é x = A . cos ( ϕo + ω . t ). Sabese que x representa a posição assumida pela partícula
em função do instante t, a partir de to = 0, A representa a
amplitude do movimento, ϕo, sua fase inicial e ω, sua
pulsação. Na figura dada, temos o gráfico da função
horária da posição de uma partícula que descreve um
M.H.S., segundo um certo referencial.
A função horária da posição dessa partícula, com dados
no S.I., é:
π π
a) x = 0,10. cos ( + .t )
2 2
π π
b) x = 0,20. cos ( + .t )
2 2
π
c) x = 0,10. cos ( .t )
2
π
d) x = 0,20. cos ( .t )
2
3π π
e) x = 0,10. cos ( + .t )
2
2
Questão 21 – Um jovem estudante resolve construir um
relógio usando uma mola de constante elástica
k=72N/m. Para que cada oscilação corresponda a um
segundo, o estudante deve prender à mola uma massa
de:
Considere π = 3
a) 1 kg
b) 2 kg
c) 3 kg
d) 4 kg
e) 5 kg
Gab: B
Questão 22 – Os ponteiros de um relógio antigo se movem
à base do movimento de um pêndulo. Esse relógio, que
funcionada corretamente, sem atrasar ou adiantar, numa
cidade X de temperaturas muito baixas, quase
negativas, foi levado para uma cidade tropical, Y, com
temperaturas bem altas, beirando os 40ºC.
Nessa cidade Y, o período do pêndulo:
a) aumentará e o relógio passará a atrasar.
b) aumentará e o relógio passará a adiantar.
c) diminuirá e o relógio passará a atrasar.
d) diminuirá e o relógio passará a adiantar.
e) não será modificado e o relógio funcionará sem
atrasar ou adiantar.
Gab: A
Questão 23 – O gráfico abaixo representa a amplitude de
um movimento harmônico simples efetuado por uma
partícula, em função do tempo.
Gab: E
Questão 20 – Experimentalmente, verifica-se que o período
de oscilação de um pêndulo aumenta com o aumento do
comprimento deste. Considere um relógio de pêndulo,
feito de material de alto coeficiente de dilatação linear,
calibrado à temperatura de 20 ºC. Esse relógio irá:
a) atrasar quando estiver em um ambiente cuja
temperatura é de 40 ºC.
b) adiantar quando estiver em um ambiente cuja
temperatura é de 40 ºC.
c) funcionar de forma precisa em qualquer
temperatura.
d) atrasar quando estiver em um ambiente cuja
temperatura é de 0 ºC.
e) atrasar em qualquer temperatura.
Gab: A
O período e a freqüência desse movimento são,
respectivamente,
a) 0,25 s e 4,0 Hz
b) 0,5 s e 2,0 Hz
c) 1,0 s e 1,0 Hz
d) 1,5 s e
e)
2
Hz
3
1,5 s e 3,0 Hz
Gab: C
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 5 de 11
Questão 24 – Uma criança de massa 30,0 kg é colocada em
um balanço cuja haste rígida tem comprimento de 2,50
m. Ela é solta de uma altura de 1,00 m acima do solo,
conforme a figura abaixo. Supondo que a criança não se
auto-impulsione, podemos considerar o sistema
"criança-balanço" como um pêndulo simples.
Desprezando-se a resistência do ar, é correto afirmar:
01. O intervalo de tempo para que a criança complete
uma oscilação é de π s.
02. A energia potencial da criança no ponto mais alto
em relação ao solo é de 150 J.
04. A velocidade da criança no ponto mais próximo do
solo é menor que 4,00 m/s.
08. Se a massa da criança fosse maior, o tempo
necessário para completar uma oscilação
diminuiria.
16. A freqüência de oscilação da criança depende da
altura da qual ela é solta.
Gab: VFVFF
Questão 25 – A elongação de um oscilador em M.H.S. varia
com o tempo, segundo o gráfico da figura 08.
(Informação para as proposições 00. e 01.)
superfícies em contato é desprezível. Estica-se a mola,
com o corpo, até o ponto A, e abandonase o conjunto
nesse ponto, com velocidade zero. Em um intervalo de
1,0 s, medido a partir desse instante, o corpo retornará
ao ponto A:
a)
b)
c)
d)
e)
uma vez.
duas vezes.
três vezes.
quatro vezes.
seis vezes.
Gab: C
Questão 27 – Em um movimento harmônico simples, a
elongação (x) é dada por x=Acos(ωt + φ). Desejando-se
percentualizar a grandeza elongação, definiu-se
%x=100x/xmax onde xmax representa o máximo valor que
a elongação pode assumir. Os percentuais (%v) e (%a)
das grandezas velocidade e aceleração, respectivamente,
receberam definições semelhantes. O gráfico desses
percentuais, em função do tempo, t(s), está representado
abaixo, com legenda posicionada na parte superior.
00. O período e a freqüência do movimento são,
respectivamente, 4s e 0,25Hz.
π 
2 
01. A função horária do movimento é x = 0,2 ⋅ sen  t 
onde x(m) e t(s).
02. A velocidade de propagação de uma onda numa
corda de 2m de comprimento, 500g de massa e sob
tração de 200N, é de 20m/s.
03. Aumentando a freqüência de uma fonte de ondas
num dado meio, o comprimento de onda diminui.
04. A ultrassonografia, muito usada na medicina para
diagnóstico
de
muitas
doenças
e
o
acompanhamento do desenvolvimento do feto
numa gestação, se baseia na propriedade que a
onda sonora tem de sofrer difração.
Gab: VVFVF
Questão 26 – Um corpo de 250 g de massa encontra-se em
equilíbrio, preso a uma mola helicoidal de massa
desprezível e constante elástica k igual a 100 N/m,
como mostra a figura ao lado. O atrito entre as
Considere as afirmativas:
I.
II.
III.
IV.
V.
O período do movimento é de 10 segundos.
A freqüência do movimento é de 0,1 hertz.
A pulsação do movimento é de π/6 rad/s.
O ângulo inicial de fase (φ) é de π/6 radianos.
A velocidade do objeto é nula no instante t=4s.
É correto afirmar que:
a) apenas a afirmativa I está correta.
b) as afirmativas I e II estão corretas.
c) apenas a afirmativa III é correta.
d) as afirmativas III e V estão corretas.
e) todas as afirmativas estão corretas.
Gab: D
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 6 de 11
Questão 28 – Uma mola de constante elástica k = 50 N/m e
massa desprezível tem uma extremidade fixa no teto e a
outra presa a um corpo de massa m = 0,2 kg. O corpo é
mantido inicialmente numa posição em que a mola está
relaxada e na vertical. Ao ser abandonado, ele passa a
realizar um movimento harmônico simples, em que a
amplitude e a energia cinética máxima são,
respectivamente,
Dado: g = 10 m/s2
a) 4 cm e 0,04 J
b) 4 cm e 0,08 J
c) 8 cm e 0,04 J
d) 8 cm e 0,08 J
e) 8 cm e 0,16 J
Gab: A
–
Questão 29 – Com relação a um pêndulo simples,
constituído por uma pequena esfera de metal de massa
m, suspensa por um fio inextensível de comprimento L
e que oscila com pequena amplitude, considere as
seguintes afirmativas:
I.
O período desse pêndulo depende da massa da
esfera.
II. A freqüência aumentará se o comprimento do fio
for aumentado.
III. Se o pêndulo completar 100 oscilações em 50 s, sua
freqüência será 2 Hz.
IV. Medindo-se o período de oscilação do pêndulo, é
possível determinar a aceleração da gravidade
local.
Assinale a alternativa correta.
a) Somente as afirmativas III e IV são verdadeiras.
b) Somente a afirmativa I é verdadeira.
c) Somente a afirmativa II é verdadeira.
d) Somente as afirmativas I e III são verdadeiras.
e) Somente as afirmativas II e IV são verdadeiras.
Gab: A
Questão 30 – Considere-se uma fonte, de freqüência igual a
10Hz, produzindo onda de amplitude igual a 2,0cm que se
propaga em uma corda com velocidade de 5,0cm/s.
A partir dessa informação, a função harmônica que
pode descrever o comportamento dessa onda, com x e y
medidos, em cm, é
01. y = 2cos2 π (10t – 2x)
02. y = 2cos2 π (0,1t – 5x)
03. y = 4cos2 π (5t – 2x)
04. y = 4cos2 π (2t – 5x)
05. y = cos2 π (0,1t – 5x)
Gab: 01
Questão 31 – Um bloco de massa m = 100 g oscila ao longo
de uma linha reta na horizontal, em movimento
harmônico simples, ligado a uma mola de constante
elástica k = 1,6 x 102 N/m. Um gráfico da posição x do
bloco em função do tempo t é mostrado na figura
abaixo.
Determine a aceleração máxima do bloco, em m/s2.
a) 10
b) 20
c) 40
d) 60
e) 80
Gab: E
Questão 32 – Um técnico de laboratório comprou uma mola
com determinada constante elástica. Para confirmar o valor
da constante elástica especificada pelo fabricante, ele fez o
seguinte teste: fixou a mola verticalmente no teto por uma
de suas extremidades e, na outra extremidade, suspendeu um
bloco com massa igual a 10 kg. Imediatamente após
suspender o bloco, ele observou que este oscilava com
freqüência de 2 Hz. Com base nesses dados, o valor da
constante elástica vale:
a) 160 π 2 N/m
b) 16 π 2 N/m
c) 1,6 π 2 N/m
d)
(16 π) 2 N/m
e)
0,16 π 2 N/m
Gab: A
Questão 33 – Um corpo oscila com movimento harmônico
simples. Sua posição, com o tempo, varia conforme a
equação x (t) = 0,30 cos (2πt + π) onde x está em metros, t
em segundos e a fase está em radianos. Assim, a frequência,
o período e a frequência angular são, respectivamente,
a)
1 Hz, 1s e 2π rad/s.
b)
π Hz,
c)
0,30 Hz, 2πs e (2πt + π) rad/s.
d)
2π Hz,
1
s e π rad/s.
π
1
s e 0,60 π rad/s.
2π
Gab: A
Questão 34 – Uma pequena pedra amarrada a uma das
extremidades de um fio inextensível de 1 m de
comprimento, preso a um galho de árvore pela outra
extremidade, oscila sob ação do vento entre dois pontos
equidistantes e próximos à vertical. Durante 10 s, observouse que a pedra foi de um extremo ao outro, retornando ao
ponto de partida, 20 vezes.
Calcule a frequência de oscilação desse pêndulo.
Gab: f = 2 Hz
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 7 de 11
Questão 35 – As posições, em metros, de uma partícula que
oscila em movimento harmônico simples em uma direção
horizontal, variam com o tempo, em segundos, de acordo
com a equação: x = 0,10cos(0,10πt + π)
Com base na equação do movimento da partícula, é correto
afirmar:
04. O comprimento de onda da onda que se propaga
na corda é de 0,25 cm.
08. A frequência de oscilação da onda que se propaga
na corda é de 40,00 Hz.
16. A velocidade de propagação da onda na corda é
de 5,00 cm/s.
Gab: 23
a)
b)
c)
d)
e)
O período da oscilação é igual a 2,0s.
A amplitude da oscilação é igual a 0,20m.
A partícula estava na posição x = 0,10m no
instante t = 0.
A aceleração da partícula tem valor máximo na
posição x = –0,10m.
A velocidade da partícula no ponto central da
trajetória é igual a zero.
Gab: D
Questão 36 – Dada a equação horária da elongação de um
π
2
Questão 39 – Um objeto preso por uma mola de constante
elástica igual a 20 N/m executa um movimento harmônico
simples em torno da posição de equilíbrio. A energia
mecânica do sistema é de 0,4 J e as forças dissipativas são
desprezíveis. A amplitude de oscilação do objeto é de:
a)
b)
c)
d)
e)
0,1 m
0,2 m
1,2 m
0,6 m
0,3 m

MHS x(t) = 4 ⋅ cos  t + π  , onde x(t) é dado em metros e t

em segundos, analise as seguintes afirmativas:
I.
A amplitude é 4 m.
II. O período é 4 s.
III. A frequência do movimento oscilatório é 0,25 Hz.
Gab: B
Questão 40 – O gráfico, a seguir, representa a elongação de
um objeto, em movimento harmônico simples, em função do
tempo:
Está CORRETO o que se afirma em
a)
b)
c)
d)
e)
I, apenas.
I e II, apenas.
I e III, apenas.
II e III, apenas.
I, II e III.
O período, a amplitude e a frequência angular valem,
respectivamente:
Gab: E
Questão 37 – Um pêndulo simples oscila com uma pequena
amplitude. Para duplicar o período do pêndulo, deve-se:
a)
b)
c)
d)
e)
quadruplicar o seu comprimento.
reduzir a sua massa pela metade.
duplicar a força usada para iniciar o movimento
do pêndulo.
duplicar a amplitude de oscilação.
duplicar o valor da massa.
Gab: A
Questão 38 – Uma onda mecânica se propaga em uma corda
homogênea de acordo com a função:
8
π

y = cos π(40 t − 8x ) +  ;
4
2

com x e y dados em centímetros e t dado em segundos.
Analise a função apresentada, as alternativas a seguir e
assinale o que for correto.
01. A amplitude máxima da onda que se propaga na
corda é de 2,00 cm.
02. O período de oscilação da onda que se propaga na
corda é de 0,05 s.
a)
b)
c)
d)
e)
2 s, 10 m e 2π rad/s.
1 s, 10 cm e π rad/s.
4 s, 20 cm e π/2 rad/s.
4 s, 10 cm e π/4 rad/s.
2 s, 10 cm e 3π/2 rad/s.
Gab: C
Questão 41 – Um oscilador massa-mola executa um
movimento harmônico simples com amplitude de 10,0 cm e
energia mecânica representada por E. Quando a elongação
do movimento for igual a 8,0 cm, a energia cinética do
movimento será igual a:
a)
b)
c)
d)
e)
20% de E.
28% de E.
36% de E.
72% de E.
64% de E.
Gab: C
Questão 42 – O gráfico abaixo representa a energia
potencial U(x), a energia cinética K(x) e a energia mecânica
total Em, em função do deslocamento de um sistema mola-
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 8 de 11
massa que executa um movimento harmônico simples. A
respeito deste evento, assinale o que for correto.
01. Na posição x = A, U(x) é máxima e K(x) é mínima.
02. Na posição x = 0, F(x) é nula e v(x) é máxima.
04. Em qualquer posição no intervalo [-A,A], Em é
nula.
08. Na posição x = 0, U(x) é máxima e K(x) é mínima.
16. Na posição x = – A, F(x) é máxima e v(x) é
mínima.
Gab: 19
Ele desloca o pêndulo para a posição A e o abandona
quando cronometra o instante t = 0. Na vigésima
passagem do pêndulo por essa posição, o cronômetro
marca t = 30 s.
a) Determine o período (T) e a freqüência (f) do
movimento desse pêndulo.
b) Esboce no caderno de respostas o gráfico x
(posição) x t (tempo) desse movimento, dos
instantes t = 0 a t = 3,0 s; considere desprezível a
influência de forças resistivas.
Gab:
a)
b)
T = 1,5 s; f = 0,67 Hz
Questão 43 – A figura a seguir mostra uma partícula P, em
movimento circular uniforme, em um círculo de raio r, com
velocidade angular constante ω , no tempo t = 0.
Questão 45 – A partir da análise da figura, que representa a
função horária do alongamento de um oscilador massa-mola
que executa um movimento harmônico simples, pode-se
afirmar:
A projeção da partícula no eixo x executa um
movimento tal que a função horária υ x ( t ) , de sua
velocidade, é expressa por:
a) υ x ( t ) = ω r
b) υ x ( t ) = ω r cos(ωt + ϕ)
c) υ x ( t ) = −ω r sen(ωt + ϕ)
d) υ x ( t ) = −ω r tg(ωt + ϕ)
01. A amplitude do movimento é igual a 2,0m.
02. O período do movimento é de 2,0Hz.
03. A freqüência do movimento é igual a 4,0s.
π
rad
2
05.A pulsação do movimento é igual a 2π rad/s .
04. A fase inicial do movimento é de
Gab: C
Questão 44 – Um estudante faz o estudo experimental de
um movimento harmônico simples (MHS) com um
cronômetro e um pêndulo simples como o da figura,
adotando o referencial nela representado.
Gab: 04
Questão 46 – Um sistema massa-molas é constituído por
molas de constantes k1 e k2, respectivamente, barras de
massas desprezíveis e um corpo de massa m, como mostrado
na figura. Determine a freqüência desse sistema.
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 9 de 11
b) é de 32 J nas extremidades e nula na posição de
equilíbrio.
c) é constante e igual a 64 J.
d) é de 32 J nas extremidades e 64 J na posição de
equilíbrio.
e) é nula nas extremidades e na posição de equilíbrio.
Gab: C
Gab: f =
1
2π
6k 1 ⋅ k 2
m( 2k 1 + 3k 2 )
Questão 47 – Duas molas idênticas de constante elástica K
são conectadas em paralelo (figura 1) e em série (figura 2) a
um bloco de massa M. Qual a razão entre o período de
oscilação das molas conectadas em paralelo e o período de
oscilação das molas conectadas em série?
Questão 49 – Um pêndulo simples de comprimento 4,0 m
possui em sua extremidade uma esfera de 2,0 kg de massa.
O pêndulo é colocado para oscilar a partir do repouso, em A.
Quando o fio estiver na vertical, passando por B, o mesmo
tem parte do seu movimento interrompido por um prego. A
esfera percorre a trajetória tracejada representada na figura,
alcançando só até o ponto C.
Em relação ao exposto, assinale a(s) proposição(ões)
CORRETA(S).
a)
b)
c)
d)
e)
2
4
1/2
1
3/4
Gab: C
TEXTO: 1 - Comum à questão: 48
Questão 48 – Um corpo de massa m está preso à
extremidade de uma mola de constante elástica K = 32 N/m
e oscila de acordo com a equação a seguir, onde todas as
variáveis estão com unidades no SI.
01. O módulo da velocidade da esfera em A é igual ao
módulo da velocidade em C.
02. A energia potencial gravitacional da esfera em A é
a mesma que em C e a variação da energia
potencial entre B e C vale 4,0 J.
04. A velocidade da esfera em B é máxima e vale 4,0
m/s.
08. A tensão no fio em C é maior do que em A.
16. A velocidade angular da esfera em A é igual à
velocidade angular em B e menor que a velocidade
angular em C.
32. O tempo que a esfera leva de A até B é igual ao
tempo de B até C, pois este tempo não depende do
comprimento do pêndulo.
X = 2 cos (3 t + π/2)
Gab: 03
Pode-se concluir que a energia mecânica do corpo
a)
Questão 50)
Um determinado tipo de sensor usado para medir
forças, chamado de sensor piezoelétrico, é colocado em
contato com a superfície de uma parede, onde se fixa
uma mola. Dessa forma, pode-se medir a força exercida
pela mola sobre a parede. Nesse contexto, um bloco,
apoiado sobre uma superfície horizontal, é preso a outra
extremidade de uma mola de constante elástica igual a
100 N/m, conforme ilustração abaixo.
é nula nas extremidades e máxima na posição de
equilíbrio.
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 10 de 11
Nessa circunstância, fazendo-se com que esse bloco
descreva um movimento harmônico simples, observa-se
que a leitura do sensor é dada no gráfico a seguir.
Com base nessas informações é correto afirmar que a
velocidade máxima atingida pelo bloco, em m/s , é de:
a)
b)
c)
d)
e)
0,1
0,2
0,4
0,8
1,0
Gab: A
Instituto Federal de Educação, Ciência e Tecnologia de Goiás – IFG – Itumbiara – Go – Prof. Frederico Mercadante – 2013
Página 11 de 11