θ θ - UFSM

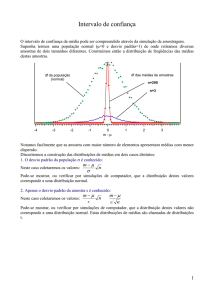
Prof. Janete Pereira Amador
1
1 Introdução
Os métodos utilizados para realização de inferências a respeito dos parâmetros
pertencem a duas categorias. Pode-se estimar ou prever o valor do parâmetro, através da
estimação de parâmetros ou pode-se tomar decisões relativas ao mesmo, através de um teste
de hipótese paramétrico (teste de significância).
O teste de significância ou teste de hipóteses paramétrico consiste em verificar se a
diferença entre um valor alegado de um parâmetro populacional e o valor de uma estatística
amostral pode ser razoavelmente atribuído a variabilidade amostral ou se a discrepância é
demasiadamente grande para ser encarada assim.
A finalidade dos testes de hipóteses paramétrico é avaliar afirmações sobre os valores dos
parâmetros populacionais.
2 Hipótese Estatística
Uma hipótese estatística é uma afirmação que pode ou não ser verdadeira sobre o valor
de um parâmetro ou sobre a distribuição de probabilidade de uma variável aleatória. Em
estatística existem dois tipos de hipótese estatística.
A Hipótese nula “H0” é a hipótese conservadora sempre pode ser expressa por uma
igualdade a zero. Por exemplo: H 0 :    0 ou H 0 :    0  0 .
A Hipótese alternativa “H1” é qualquer hipótese que diferi de uma dada hipótese nula é a
Hipótese experimental. Por exemplo: H 1 :    0 ou H 1 :    0 ou H 1 :    0 .
A Hipótese nula “H0” é uma afirmação que diz que o parâmetro populacional é tal
como especificado (isto é, a afirmação é verdadeira).
A Hipótese alternativa “H1” é uma afirmação que oferece uma alternativa à alegação
(Isto é, o parâmetro é maior ou menor que o valor alegado)
As hipóteses “H0” e “H1” são mutuamente excludentes, aceitando-se uma hipótese como
verdadeira, a outra, automaticamente, será rejeitada. Portanto deve-se tomar cuidado para
não ser cometido erros com relação aceitação e rejeição de “H0” e “H1”.
3 Tipos de Erro
Quando se realiza um teste de hipótese, pode-se cometer dois tipos de erro:
­ Erro tipo I: consiste em rejeitar “H0” quando ela é verdadeira. Pode ser
limitado pela escolha do nível de significância  que probabilidade de
rejeitar “H0” quando essa for verdadeira.
­ Erro tipo II: Consiste em aceitar “H0”, quando ela é falsa.
O nível de significância do  teste (probabilidade de rejeitar “H0” quando essa for
verdadeira) é fixada antes da extração das amostras. Os valores mais comuns para  são:
0.01, 0.05 e 0.10 ou 1%, 5% e 10%. Se por exemplo, ao delinear-se um teste, escolhe-se 
= 0.05 ou 5%, significa que em cerca de 5% rejeitar-se-ia erroneamente H0.
O coeficiente de confiança, indicado por (1 -  ), é a probabilidade de que a hipótese
nula H0 não seja rejeitada quando de fato for verdadeira e não deve ser rejeitada. Em
termos de metodologia do teste de hipóteses, esse coeficiente representa a probabilidade de
Prof. Janete Pereira Amador
2
se concluir que o determinado valor do parâmetro que está sendo testado para hipótese nula
seja plausível.
4 Teste de Hipóteses Unilateral e Bilaterais
Dependendo da hipótese alternativa, os testes são classificados como unilaterais e
bilaterais.
4.1 Teste de hipóteses bilateral
Os testes bilaterais se usam sempre que há divergência crítica em ambas as direções,
tal como ocorreria na fabricação de roupas, onde camisas muito grandes ou muito
pequenas não correspondem à determinação do padrão. Outro exemplo é o caso em que
peças devem ajustar-se uma a outra, como o parafuso e porca. Uma variação excessiva
ocasionará seja um ajuste muito frouxo, de modo que as peças não permanecerão unidas,
ou um ajuste excessivo impedindo a conjugação das peças. Assim por exemplo:
­ H 0 :    0 contra H 1 :    0 é um teste bilateral, esquematicamente:
Valor
tabelado
também
chamado de valor crítico, separa
a região de aceitação H0 (RA H0)
da região de rejeição (RR H0).
4.2 Teste de hipóteses unilateral a direita
O teste unilateral a direita é útil para testar se determinado padrão máximo não foi
excedido Como exemplo seria: teor máximo de gordura permitida em determinado tipo de
leite, radiação emitida por usinas nucleares, número de passas defeituosas de uma remessa
de certa mercadoria, quantidade de poluição atmosférica emitida por uma determinada
fabrica. Assim por exemplo:
H 0 :    0 contra , H 1 :    0 (  0 é o valor suposto para o parâmetro) é um teste
unilateral a direita, esquematicamente:
Prof. Janete Pereira Amador
3
4.2 Teste de hipóteses unilateral a esquerda
O teste unilateral a esquerda é útil para verificar se determinado padrão mínimo foi
atingido. Como exemplo seria: conteúdo mínimo de gordura no leite, peso líquido de
pacotes de determinado produto, vida de um produto tal qual como especificado no
certificado de garantia. Assim por exemplo:
­ H 0 :    0 contra H 1 :    0 é um teste unilateral a esquerda,
esquematicamente:
5 Procedimentos para Realização de um Teste de Hipóteses
Para realizar um teste de hipótese sugere-se seguir as seguintes etapas:
1) Formular as hipóteses;
2) Identificara a estatística do teste;
3) Determinar o nível de significância;
4) Calcular a estatística utilizando os valores amostrais;
5) Comparar as estatística calculada com a estatística tabelada;
6) Concluir.
5.1 Teste de hipóteses para média 
O objetivo do teste de significância para médias é avaliar afirmações feitas a
respeito de médias populacionais. Há basicamente três tipos de afirmação que se podem
fazer a cerca das médias populacionais e cada tipo requer um tipo diferente de avaliação.
Uma afirmação pode dizer respeito a média de uma única população; a avaliação envolve
então um teste de uma amostra. Ou pode-se afirmar que a média de duas populações são
iguais; tem-se então um teste de duas amostras. Finalmente pode-se afirmar que a as
médias de mais de duas populações são iguais, o que envolve um teste de K amostras
Análise de Variância.
5.1.1. Teste de significância de uma amostra para uma média  amostral contra um
valor paramétrico
De acordo com o teorema do limite central, se obtemos amostras grandes (n > 30)
(de qualquer população com qualquer distribuição), a distribuição das médias pode ser
aproximada por uma distribuição normal. Sendo assim, distribuição das médias amostrais
será aproximadamente normal com media  e desvio padrão 
n.

Em um teste de hipóteses, o valor de
corresponde a hipótese nula, e o valor do
desvio padrão populacional deve ser conhecido. Se  é desconhecido e as amostras são
Prof. Janete Pereira Amador
4
grandes ( n  30 , podemos usar o desvio padrão amostral “S” em substituição σ , porque
grandes amostras aleatórias tendem a representar a população com distribuição normal.
 Retira-se uma amostra de tamanho n e calcula-se X .
X  0

n
Teste de significância para a diferença entre duas médias populacionais
independentes

Calcula-se o valor da estatística Z c 
Os testes de duas amostras são usados para decidir se as médias de duas populações
são iguais. Para a realização do teste exige que as duas amostras sejam independentes, uma
de cada população. Duas amostras são independentes se a amostra extraída de uma das
populações não tem qualquer relação com a amostra extraída da outra.
Esses testes são freqüentemente usados para comparar dois métodos de ensino, duas
marcas, duas cidades, dois distritos escolares, e outros casos análogos.
Ao testar as hipóteses para diferença entre duas médias supõe-se que:
­ As duas amostras são independentes
O tamanho das duas amostras são grandes n 1 > 30 e n2 > 30 e/ou as variâncias são
x1  x 2 
conhecidas utiliza-se a estatística Z c 
.
 12  22

n1 n 2
Quanto às hipóteses temos que:
A hipótese nula pode ser de que as duas populações tem médias iguais.
H 0 : 1   2
Enquanto que as alternativas podem ser:
H 1 : 1   2 ;
H 1 : 1   2 e H1 : 1   2 note que:
H 1 : 1   2 é equivalente a H 1 : 1   2
Ex: Exemplo: Suponhamos um teste de inteligência aplicado a 318 meninos e 197
meninas de 13 anos de idade, obtendo-se os seguintes resultados:
x1 =38;  1  12 (desvio padrão)
x 2 =36  2 = 13
  0,05
Exercício 1: Examinaram duas classes constituídas de 40 e 50 alunos, respectivamente. Na
primeira, a média foi 74 com desvio padrão 8. Enquanto que na Segunda a média foi 78 com
desvio padrão 7. Há uma diferença significativa entre os aproveitamentos das duas classes no
nível de significância de 5 %?
Exercício 2 : A altura média de 50 estudantes do sexo masculino que tiveram participação
superior à média nas atividades atléticas colegiais era de 178,23 cm, com desvio padrão de
6,35 cm. Enquanto que os 50 que não mostraram nenhum interesse nessas atividades
apresentaram a altura média de 175,45 cm, com desvio de 7,11 cm. Testar a hipótese dos
estudantes do sexo masculino que participam de atividades atléticas serem mais altos que os
demais. Adote alfa = 1 %
Prof. Janete Pereira Amador
5
Exercício 3 : No estudo de efeito de doses diárias de vitamina C sobre os resfriados registrouse o número de resfriados contraídos por cada participante durante um certo período de tempo
experimental, resultando no quadro abaixo:
Pergunta-se: as doses diárias de vitamina C têm efeito sobre o no de resfriados contraídos?
Adote alfa = 5 %.
Teste de Hipótese para proporção
Os testes para proporções são adequados quando os dados sob análise consistem em
contagens ou freqüências de itens em duas ou mais classes. A finalidade de tais testes é
avaliar afirmações sobre a proporção ou percentagem de uma população. Os testes se
baseiam na premissa de que uma proporção amostral, isto é, x ocorrências em n
observações, ou x/n, será igual a verdadeira proporção populacional. Os testes focalizam
geralmente as diferenças entre um número esperado de ocorrências (supondo-se verdadeira
uma afirmação) e o número efetivamente observado. A diferença é então comparada com a
variabilidade prescrita por uma distribuição amostral baseada na hipótese de que H0 é
realmente verdadeira.
Seja  a proporção dos elementos de uma população que possuem uma
determinada característica. Por exemplo,  é igual a proporção ou percentagem dos
habitantes, de uma determinada localidade, que possuem automóvel. Se quisermos testar a
hipótese de que essa proporção é igual a determinado valor, contra a alternativa dessa
proporção ser maior de que o valor especificado, lança-se as hipóteses:
H0:  =  0
Contra uma das hipóteses alternativas:
H1 :  >  0
H1 :    0
H1 :    0
Um bom estimador do parâmetro  é a proporção amostral P, que para grandes
amostras segue uma distribuição aproximadamente normal com média  e a variância
 (1   )
 (1  ) 
ou seja, P ~ N ,
.
n
n 

Portanto pode-se usar a variável normal padronizada.
P 
~ N (0,1)
Z 
sendo:
 (1   )
n
número de sucessos na amostra
x
P=
=
n
tamanho da amostra
  proporção de sucesso a partir da hipótese nula
Para proceder ao teste de hipóteses, como nos casos anteriores, o valor de Zc.
calculado deve ser comparado com o de Z  dado em função de  , o nível de significância
do teste.
Prof. Janete Pereira Amador
6
Exemplo 1 O fabricante de uma droga medicinal afirma que ela é 90 % eficaz na cura de
uma alergia, em um período de 8 horas. Em uma amostra de 200 pessoas que tinham
alergia a droga curou 160 pessoas. Determine se a afirmação do fabricante é verdadeira ?
Usar alfa = 5 %.
Exemplo 2: A experiência tem demonstrado que 60 % dos estudantes são aprovados num
exame de inglês para admissão a uma universidade. Se 60 dos 110 estudantes de uma
certa cidade fossem aprovados, pode-se concluir que estes estudantes são inferiores em
inglês ? Usar alfa = 1 %.
Exercício 1: A proporção de aprovação ao final do ano nas escolas da periferia de São
Paulo é de 86 %. Dos 200 alunos de uma escola localizada nessa região a proporção de
aprovados foi de 92 %. Pode-se afirmar que os alunos dessa escola são melhores que os
outros ? Usar alfa = 5 %.
Resposta: ao nível de 5 %, unicaudal, rejeita-se a hipótese. Os estudantes dessa escola são
mesmo melhores que os demais.
Exercício2: Uma amostra de 200 proprietários de carro de uma cidade mostrou que
48 deles tinham sido multados naquele ano. A média anual nacional é de 30 % dos
motoristas são multados por ano. Pode-se afirmar que os motoristas dessa cidade são
menos infratores que os demais ? Usar alfa = 5 %.
Resposta: ao nível de 5 %, unicaudal, rejeita-se a hipótese. Os motoristas dessa cidade são
menos infratores que a maioria.
Exercício 3: Se você lançar um dado 240 vezes e obtiver 52 seis, concluirá que o dado
favorece o número seis ? Usar alfa = 5 %.
Resposta: ao nível de 5 %, unicaudal, rejeita-se a hipótese. O dado favorece o seis.
Prof. Janete Pereira Amador
7
EXERCÍCIOS COMPLEMENTARES
Teste da Média
1) No exame de inglês TOEFL (Test of English as a Foreign Language)
utilizado por alunos estrangeiros para ingressar nas faculdades americanas,
verificou-se através dos anos anteriores que a média obtida foi de 450 pontos.
Em 2002, 136 brasileiros realizaram o teste e obtiveram uma média de 465
pontos com desvio padrão de 80 pontos. Pode-se concluir, no nível de significância
de 5% que os brasileiros possuem um melhor desempenho nesse teste ?
Resposta: Sim
2) Em uma pesquisa verificou-se que em média os estudantes universitários
estudam em casa 8 horas por semana. Em uma faculdade, 36 alunos foram
entrevistados e resultou em uma média de 7,5 horas de estudo semanal com um
desvio padrão de 2 horas. Pode-se dizer, com um nível de significância de 5%,
que esses alunos estudam menos que os demais?
Resposta: Não
Teste de Proporção
3) Em 1990, 5,8 % dos candidatos a emprego submetidos a um teste de drogas foram
reprovados. Em 2000, 58 dos 1520 candidatos foram também reprovados no teste.
Pode-se concluir que houve diminuição, aumento, ou ficou inalterado do uso de
drogas ?  = 5%
Resposta: Diminuição
4) Em 2000, o IBGE observou que 9 % dos estudantes no Brasil que terminavam o
segundo grau, ingressavam na faculdade. Em Lorena, 60 dos 500 secundaristas
entrevistados se matricularam na faculdade. Pode-se concluir que Lorena está
acima da média nacional em relação a porcentagem de estudantes ingressantes na
faculdade ?  = 5%
Resposta: Sim, está.
Teste da diferença entre médias
5) ) Considere o quadro abaixo e responda: Pode-se concluir que as crianças nascidas
em hospital particular são mais pesadas do que as crianças nascidas em hospital
público? = 1%
Resposta: Não
Prof. Janete Pereira Amador
8
6) Considere o quadro abaixo e responda: Pode-se concluir que os estudantes de
escolas públicas tiram notas inferiores aos da escola particular num exame de
vestibular ? adote = 5%
Resposta: Sim.