1ª Prova de Física II - FCM0102 - IFSC

1ª Prova de Física II - FCM0102
#USP:
Nome:
30 de agosto de 2012
1. (2,5 pontos) Pretende-se encher um balde usando uma torneira de vazão I =
1, 0 × 10−5 m3 /s. Entretanto, o fundo do balde possui um furo de área A = 5, 0 mm2
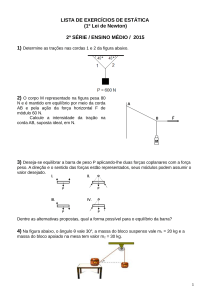
por onde a água vaza (vide Fig. 1).
(a) (2,0 pontos) Qual é a altura máxima h que a água atinge dentro do balde? Assuma
escoamento laminar e despreze a viscosidade da água.
(b) (0,5 ponto) Se o fluxo fosse viscoso, a altura atingida seria maior ou menor que
no item (a)? Justifique.
2. (2,5 pontos) Um recipiente cilíndrico está cheio até a borda de um líquido de
densidade ρ. Quando o recipiente é colocado em uma balança, o peso medido é W .
Uma esfera de massa m e volume V , com densidade menor do que a do líquido, é
empurrada lentamente para dentro do líquido usando uma barra rígida muito fina até
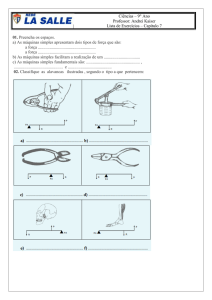
que a esfera esteja completamente submersa como mostra a figura 2(a).
(a) (0,5 ponto) Qual é a massa do líquido que transbordou enquanto a esfera era
mergulhada?
(b) (1,0 ponto) Qual é a leitura da balança quando a esfera está completamente submersa, assumindo que todo o fluido que transbordou foi retirado da balança? Sugestão:
pense nas forças sobre a balança, sobre o líquido e sobre a esfera segundo as leis de
Newton.
(c) (1,0 ponto) Se ao invés de ser empurrada por uma barra fina, a esfera for presa
ao fundo do recipiente por uma corda muito fina (vide Fig. 2(b)), qual será a leitura da
balança depois que todo o fluido que transbordou for retirado da balança?
I
h
v
Figura 1: Balde com vazamento.
(a)
(b)
Figura 2:
puxo.
Balança e em-
3. (2,5 pontos) Considere um planeta líquido, formado por uma distribuição esfericamente simétrica de massa de um fluido incompressível de densidade ρ. Se o raio do
planeta é R e a pressão se anula na superfície (não há atmosfera), calcule a pressão
dentro do planeta em função da distância r ao centro.
Dica 1: a derivada da pressão é igual à densidade de força volumétrica.
Ou dica 2: a pressão em um ponto é dada pelo peso da coluna de fluido acima daquele
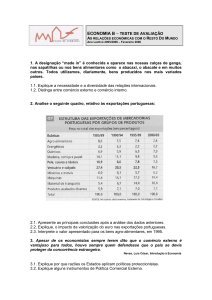
ponto (vide fig. 3).
r
R
4. (2,5 pontos) Imagine um “cabo espacial” (“skyhook ”) que consiste de uma longa
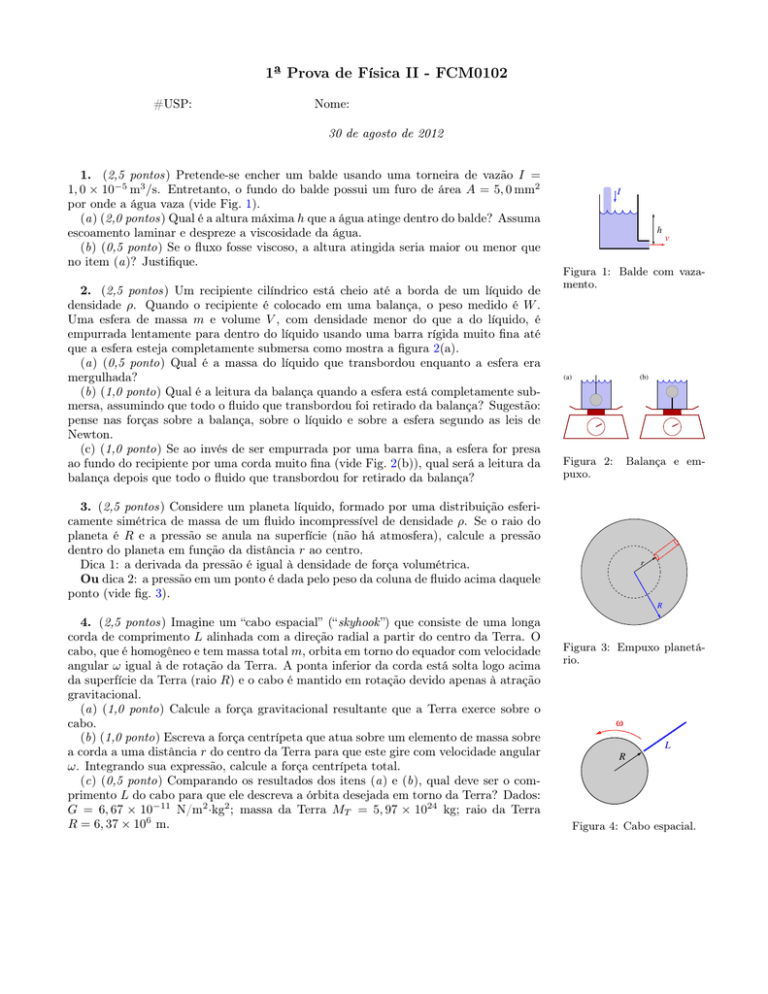
corda de comprimento L alinhada com a direção radial a partir do centro da Terra. O
cabo, que é homogêneo e tem massa total m, orbita em torno do equador com velocidade
angular ω igual à de rotação da Terra. A ponta inferior da corda está solta logo acima
da superfície da Terra (raio R) e o cabo é mantido em rotação devido apenas à atração
gravitacional.
(a) (1,0 ponto) Calcule a força gravitacional resultante que a Terra exerce sobre o
cabo.
(b) (1,0 ponto) Escreva a força centrípeta que atua sobre um elemento de massa sobre
a corda a uma distância r do centro da Terra para que este gire com velocidade angular
ω. Integrando sua expressão, calcule a força centrípeta total.
(c) (0,5 ponto) Comparando os resultados dos itens (a) e (b), qual deve ser o comprimento L do cabo para que ele descreva a órbita desejada em torno da Terra? Dados:
G = 6, 67 × 10−11 N/m2 ·kg2 ; massa da Terra MT = 5, 97 × 1024 kg; raio da Terra
R = 6, 37 × 106 m.
Figura 3: Empuxo planetário.
ω
L
R
Figura 4: Cabo espacial.
2
GABARITO:
1.
(a) O nível da água no balde sobe até que a vazão de saída se iguale à vazão de entrada. Se v é a velocidade com
que a água sai do furo, a condição é
I = Av.
O valor de v é dado pela equação de Bernoulli. Tomando o ponto 1 sobre a superfície da água dentro do balde, temos
p1 = patm , z1 = h (para altura medida a partir do fundo do balde) e v1 = 0. Tomando o ponto 2 logo na saída do
furo, temos p2 = patm , z2 = 0 e v2 = v. Usando a equação de Bernoulli:
1
1
p1 + ρv12 + ρgz1 = p2 + ρv22 + ρgz2 ,
2
2
⇒
ρgh =
1 2
ρv ,
2
⇒
h = 20 cm .
⇒
v=
p
2gh.
Substituindo na condição de equilíbrio das vazões, obtemos
I=A
p
2gh,
⇒
h=
I2
,
2gA2
(b) A altura seria maior. Para uma dada altura h, a velocidade na saída pelo furo diminui quando o fluido é
viscoso porque parte da energia potencial gravitacional no ponto 1 sobre a superfície é dissipada em calor durante o
escoamento. Por isso o fluido tem de partir de uma altura maior para atingir a mesma velocidade v na saída tal que
Av = I.
2.
(a) A esfera desloca um volume V de líquido quando submersa. A massa desse volume de líquido é
M = ρV
(b) A leitura W1 da balança é igual ao módulo da força que o líquido exerce sobre ela (podemos imagniar que o
fundo do recipiente está colado à balança). Como o líquido está em equilíbrio, a soma das forças sobre ele deve ser
nula. Denotando por ẑ o vetor unitário na direção vertical para cima, existem três forças sobre o líquido: (i ) a reação
da força sobre a balança, que aponta para cima e é dada por W1 ẑ; (ii ) o peso do próprio líquido que sobrou, dado por
~ = −ρgV ẑ
−(W − ρV g)ẑ; (iii ) a força que a esfera exerce sobre o líquido, que é a reação do empuxo e é dada por −E
(pois se o líquido empurra a esfera para cima, a esfera empurra o líquido para baixo). Para que o líquido esteja em
equilíbrio, devemos ter
W1 − (W − ρV g) − ρgV = 0,
⇒
W1 = W
(c) Neste caso, a leitura W2 da balança é igual em módulo à força que o líquido exerce sobre ela menos a tensão T
na corda, que puxa a balança para cima. A força que o líquido exerce sobre a balança é determinada pela condição
de equilíbrio do líquido e é a mesma força de módulo W1 do item anterior. Para que a esfera esteja em equilíbrio, o
módulo T da tensão na corda deve ser tal que
T + mg = E = ρV g,
⇒
T = ρV g − mg.
Logo a leitura da balança neste caso é
W2 = W1 − T,
⇒
W2 = W − ρV g + mg.
Como m < ρV pois a esfera é menos densa do que o fluido, temos W2 < W .
3.
A densidade de força gravitacional num ponto que dista de r do centro pode ser calculada usando o teorema das
cascas esféricas:
2
GM (r)ρ
4πGrρ
f~ = −
r̂ = −
r̂,
2
r
3
onde G é a constante da gravitação universal. Usando a dica 1, temos que
4πGrρ2
dP
=−
,
dr
3
⇒
P (r) = cte −
2πGρ2 2
r ,
3
3
onde a constante de integração pode ser calculada usando a condição de contorno de que na superfície do planeta
P (r = R) = 0. Logo,
P (r) =
2πGρ2
R2 − r 2 .
3
Pode-se chegar no mesmo resultado usando a dica 2. Nesse caso, devemos calcular o peso W da coluna de fluido
ilustrada na fig. 3. Novamente usando o teorema das cascas esféricas encontramos que
ˆ
~ =
W
r
R
GM (r0 )ρAdr0
4π
−
r̂ =
GAρ2
02
r
3
ˆ
R
−r0 dr0 r̂,
⇒
W =
r
2πGρ2
R2 − r2 A,
3
onde A é a área da base do cilindro. A pressão é então dada por
P =
W
2πGρ2
R2 − r 2 ,
+ P0 =
A
3
onde P0 = 0 é a pressão na superfície do planeta.
4.
(a) Integrando a atração gravitacional entre o planeta e os elementos de massa ρdx do cabo, encontramos que
ˆ
R+L
F~G = −
R
GM ρdx
r̂,
x2
⇒
GM m
r̂ ,
F~G = −
R (R + L)
onde ρ = m/L é a densidade do cabo.
(b) A força centrípeta em um elemento de massa do cabo que dista de x do centro do planeta e tem comprimento
dx é igual a
−acp dmr̂ = −ρω 2 xdxr̂.
Integrando a expressão acima,
ˆ
R+L
F~cp = −
ρω 2 xdxr̂,
⇒
R
1
F~cp = − mω 2 (2R + L) r̂ .
2
(c) Igualando FG = Fcp , temos que
1 2
GM
ω (2R + L) =
,
2
R (R + L)
⇒
3R
L=−
+
2
s
2GM
+
Rω 2
R
2
onde a solução negativa não tem sentido físico. Substituindo os valores dados,
L = 1, 44 × 108 m,
que é em torno de 37% da distância entre a Terra e a Lua, ou 23 vezes o raio da Terra.
2
,