Capítulo 3

Introdução ao Cálculo
Capítulo 3 – Derivada
3.1 – Reta Tangente e Taxa de Variação
Exemplo nr. 1 - Uma partícula caminha sobre uma trajetória
qualquer obedecendo à função horária:
s(t) = 3t2 – 5t + 2 (s em metros , t em segundos)
a) Qual a velocidade média da partícula no intervalo de
tempo [ 2 , 4 ]?
b) Qual a velocidade média da partícula no intervalo de
tempo [ 2 , 3 ] ?
c) Qual a velocidade média da partícula no intervalo de
tempo [ 2 ; 2,1 ]?
d) Qual a velocidade média da partícula no intervalo de
tempo [ 2 , (2 + ∆t) ], com ∆t ≠ 0?
e) Qual a velocidade da partícula no instante t = 2 s?
–
65 –
Introdução ao Cálculo
Resolução:
a) Velocidade média de uma partícula num certo intervalo
de tempo é definida pelo quociente entre o espaço
percorrido (∆s = sfinal – sinicial) e o intervalo de tempo
gasto em percorrê-lo (∆t = tfinal – tinicial):
vm =
∆s
∆t
∆s = s (4) − s (2) = (3.42 − 5.4 + 2) − (3.22 − 5.2 + 2)
∆s = 30 − 4 = 26 m
∆t = 4 − 2 = 2 s
26
Logo : vm =
= 13 m / s
2
b) Neste item, temos:
vm =
∆s
∆t
∆s = s (3) − s (2) = (3.32 − 5.3 + 2) − (3.22 − 5.2 + 2)
∆s = 14 − 4 = 10 m
∆t = 3 − 2 = 1 s
10
Logo : vm =
= 10 m / s
1
–
66 –
Introdução ao Cálculo
c) Neste item, temos:
∆s
∆t
∆s = s (2,1) − s (2)
vm =
∆s = (3.2,12 − 5.2,1 + 2) − (3.22 − 5.2 + 2)
∆s = 4,73 − 4
∆s = 0,73 m
∆t = 2,1 − 2 = 0,1 s
Logo : vm =
0,73
= 7,3 m / s
0,1
d) Neste item, temos:
∆s = s (2 + ∆t ) − s (2)
∆s = [3.(2 + ∆t )2 − 5.(2 + ∆t ) + 2] − (3.22 − 5.2 + 2)
∆s = [4 + 7∆t + 3∆t 2 ] − 4
∆s = 7∆t + 3∆t 2
Logo : vm =
7∆t + 3∆t 2
ou seja, vm = 7 + 3∆t
∆t
Observe que este item com ∆t genérico engloba os itens
anteriores:
Item a) ∆t = 2 s
⇒ vm = 7 + 3.2 = 13 m/s
Item b) ∆t = 1 s
⇒ vm = 7 + 3.1 = 10 m/s
Item c) ∆t = 0,1 s
⇒ vm = 7 + 3.0,1 = 7,3 m/s
–
67 –
Introdução ao Cálculo
e) No item anterior obtivemos a velocidade média da
partícula no intervalo de tempo [2, (2 + ∆t)], com
∆t ≠ 0. Quando ∆t tende a zero, o segundo extremo de
intervalo de tempo tende a 2 e o referido intervalo tende
a [2, 2], que é um “intervalo de amplitude nula”,
caracterizando o instante t = 2 s.
Logo, fisicamente, quando ∆t tende a zero, a velocidade
média tenderá para a velocidade instantânea da
partícula para t = 2s e esta velocidade será denotada por
v(2).
Portanto, concluímos que: v(2) = lim 7 + 3∆t = 7 m / s
∆t → 0
Exemplo nr. 2 - (FLEMMING, página 246, exemplo 2) Uma cidade
X é atingida por uma moléstia epidêmica. Os setores de saúde
calculam que o número de pessoas atingidas pela moléstia
depois de um tempo t (medido em dias a partir do primeiro dia
da epidemia) é, aproximadamente, dado por:
n(t ) = 64t −
t3
3
a) Qual a razão da expansão da epidemia no tempo t =4?
b) Qual a razão da expansão da epidemia no tempo t =8?
c) Quantas pessoas são atingidas pela epidemia no 5o dia?
Resolução:
A taxa com que a epidemia se propaga é dada pela razão de
variação da função n(t) em relação a t.
–
68 –
Introdução ao Cálculo
a) Para t = 4
Resolução por limite:
n(t + 4) − n(4)
n(t + 4) − n(4)
= lim
=
t
t →0 (t + 4) − 4
t →0
lim

(t + 4)3  
(4)3 
64(t + 4) −
 − 64.4 −

3  
3 

lim
=
t
t →0
64t + 256 −
lim
t →0
(t 3 + 12t 2 + 48t + 64)
− 234,67
3
=
t
144t − t 3 − 12t 2
= 48 pessoas / dia
3t
t →0
lim
Resolução pela regra de derivação:
n(t ) = 64t −
t3
3
dn
= 64 − t 2 = 64 − (4)2 = 48 pessoas / dia
dt
–
69 –
Introdução ao Cálculo
b) Para t = 8
Resolução por limite:
n(t + 8) − n(8)
n(t + 8) − n(8)
= lim
=
t
t →0 (t + 8) − 8
t →0
lim

(t + 8)3  
(8)3 
+
−
64
(
t
8
)
−
64
.
8
−

 

3  
3 

lim
=
t
t →0
64t + 512 −
lim
t →0
(t 3 + 24t 2 + 192t + 512) 1024
−
3
3 =
t
− t 3 − 16t 2
= 0 pessoas / dia
3t
t →0
lim
Resolução pela regra de derivação:
n(t ) = 64t −
t3
3
dn
= 64 − t 2 = 64 − (8)2 = 0 pessoas / dia
dt
–
70 –
Introdução ao Cálculo
c) Para calcularmos quantas pessoas foram atingidas pela
epidemia no 5o dia, basta calcular n(5) – n(4):

(5)3  − 64(4) − (4)3 
n(5) − n(4) = 64(5) −
 

3  
3 

n(5) − n(4) = 43,6 pessoas / dia
Exemplo nr. 3 - Uma partícula se move segundo a função
s = 2t4 + 8t3. Em que instante sua aceleração é nula? (tempo em
segundos)
Resolução:
Sabemos que a velocidade de uma partícula é dada pela
derivada do espaço em função do tempo:
v=
ds
= 8t 3 + 24t 2
dt
E que a aceleração é a derivada da velocidade em função do
tempo:
a=
dv
= 24t 2 + 48t
dt
Igualando a aceleração a zero temos os instantes em que a
aceleração é nula.
24t 2 + 48t = 0
t (24t + 48) = 0
t=0
t = −2 (não é possível )
–
71 –
Introdução ao Cálculo
Exemplo nr. 4 - (ANTON,
página 175, exemplo 2) O fator
limitante na resistência
atlética é o desempenho
cardíaco, isto é, o volume
de sangue que o coração
pode
bombardear
por
unidade de tempo durante
uma competição atlética. A
figura ao lado mostra um gráfico de teste de esforço de
desempenho cardíaco V em litros (L) de sangue versus a
quantidade de trabalho que está sendo feita W em kilogramasmetros (kg.m) durante um minuto de levantamento de peso.
Este gráfico ilustra o conhecido fato médico de que o
desempenho cardíaco aumenta com a quantidade de trabalho
mas, depois de atingir um valor de pico, começa a cair.
a) Use a reta secante da
figura a para estimar a
taxa
média
de
desempenho cardíaco
em relação ao trabalho
a ser executado quando
este aumenta de 300
para 1200 kg.m.
b) Use a reta tangente da
figura b para estimar a
taxa
de
variação
instantânea
do
desempenho cardíaco
em relação ao trabalho
que
está
sendo
executado no ponto
onde ele é de 300 kg.m.
–
72 –
Introdução ao Cálculo
Resolução:
a) Usando os pontos estimados (300, 13) e (1200, 19), a
inclinação da reta secante da figura 1 é:
msec ≈
19 − 13
L
≈ 0,0067
1200 − 300
kg .m
Dessa forma, a taxa de variação média de desempenho
cardíaco em relação ao trabalho que está sendo
executado no intervalo dado é de aproximadamente
0,0067 L / kg.m.
Isso significa que, em média, o aumento de 1 unidade
no trabalho que está sendo executado produz um
aumento de 0,0067 L, no desempenho cardíaco no
intervalo dado.
b) Usando a reta tangente estimada na figura 2 e os pontos
estimados (0,7) e (900,25) sobre esta reta obtemos:
mtg ≈
25 − 7
L
≈ 0,02
900 − 0
kg .m
Assim, a taxa de variação instantânea do desempenho
cardíaco, em relação ao trabalho é de aproximadamente
0,02 L / kg.m.
–
73 –
Introdução ao Cálculo
Exercícios:
1) Uma partícula move-se sobre uma reta de forma que, após t
segundos ela está a s = 2t2 + 3t centímetros de sua posição
inicial.
a) Determine a posição da partícula após 2 s.
b) Determine a posição da partícula após 3s.
c) Calcule a velocidade média da partícula no intervalo de
tempo [2 , 3].
d) Calcule a velocidade instantânea em t = 2.
2) Um projétil é disparado diretamente para cima e, nos
primeiros 30 segundos, a altura atingida por ele em t
segundos é de h = 4t2 metros.
a) Qual a altura atingida em 20s?
b) Qual a velocidade média do projétil nos primeiros 30s?
c) Qual a velocidade instantânea após 30s?
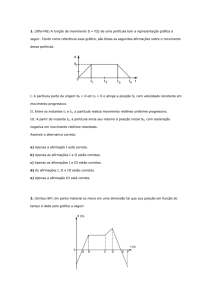
3) A figura abaixo mostra a curva “posição x tempo” de uma
plataforma que se move para cima até 60 metros e pára.
70
Distância ( m )
60
50
40
30
20
10
0
0
5
10
15
20
25
Tempo ( s )
a) Calcule a velocidade instantânea da plataforma quando
t = 15s.
–
74 –
Introdução ao Cálculo
b) Esboce a curva da velocidade x tempo para o
movimento do plataforma no intervalo 0 ≤ t ≤ 20 .
4) Um objeto cai em direção ao solo de altura de 180 metros.
Em t segundos, a distância percorrida pelo objeto é de
s = 20t2 m.
a) Quantos metros o objeto percorre após 2 segundos?
b) Qual é a velocidade média do objeto nos 2 primeiros
segundos?
c) Qual é a velocidade instantânea do objeto em t = 2 s?
d) Quantos segundos o objeto leva para atingir o solo?
e) Qual é a velocidade média do objeto durante a queda?
f) Qual é a velocidade instantânea do objeto quando ele
atinge o solo?
5) A população de determinado país (N) em milhões de
habitantes cresceu segundo o gráfico abaixo. Use uma reta
tangente estimada da figura no ponto onde t = 1950 para
aproximar o valor da derivada. Descreva o seu resultado
como uma taxa de variação.
população (em milhões)
6000
5000
4000
3000
2000
1000
0
1850
1900
1950
tempo (em anos)
–
75 –
Introdução ao Cálculo
6) A população inicial de uma colônia de bactérias é 10.000.
Depois de t horas a colônia terá a população P(t) que
obedece a lei: P(t) = 10.000.1,2t.
a) Qual o número de bactérias depois de 10 horas?
b) Encontre a lei que dá a variação da população P em
relação ao tempo t.
c) Determine essa variação instantânea após 10 horas.
7) Sabemos que o volume de um cubo é função de seu lado.
Determine:
a) A taxa média de variação do cubo em relação ao lado
quando este cresce de 3 para 5.
b) A taxa de variação do volume em relação ao lado
quando este mede 5.
8) Um tanque está sendo esvaziado segundo a função
V(t) = 200.(30 – t)2, onde o volume é dado em litros e o
tempo em minutos. A que taxa a água escoará após 8
minutos? Qual a taxa média de escoamento durante os
primeiros 8 minutos?
9) Uma saltadora de pára-quedas pula de um avião. Supondo
que a distância que ela cai antes de abrir o pára-quedas é de
s(t) = 986.(0,835t – 1) + 176t , onde s está em pés e t em
segundos, calcule a velocidade instantânea (em m/s) da
pára-quedista quando t = 15. (Obs.: 1 pé = 0,3048 m)
10) As posições de dois móveis num instante t segundos são
dadas por s1 = 3t3 – 12t2 +18t + 5 m e s2 = -t3 + 9t2 – 12t m.
Em que instante as partículas terão a mesma velocidade?
11) O gráfico a seguir mostra a posição de um carro
percorrendo uma rodovia. O motorista parte em t = 0 e
retorna 15 horas mais tarde.
–
76 –
Introdução ao Cálculo
600
posição (em km)
500
400
300
200
100
0
0
5
10
15
tempo (em horas)
a) Construa o gráfico da velocidade do carro v = ds/dt para
0 ≤ t ≤ 15.
b) Construa o gráfico da velocidade do carro a = dv/dt
para 0 ≤ t ≤ 15.
c) Supondo que s = 15t2 – t3, faça os gráficos da
velocidade e aceleração, comparando-os com os
resultados dos itens a e b.
12) Um objeto se move de modo que no instante t a distância é
dada por s = 3t4 – 2t. Qual a expressão da velocidade e da
aceleração desse objeto?
13) Achar a velocidade e a aceleração no instante t = 3
segundos onde s = 3t3 – 2t2 + 2t +4 é a função que informa
a posição (em metros) de um corpo no instante t.
14) Um corpo se desloca sobre um plano inclinado através da
equação s = 5t2 – 2t (s em metros e t em segundos).
Calcular a velocidade e a aceleração desse corpo após 2
segundos da partida.
–
77 –
Introdução ao Cálculo
15) Um corpo é abandonado do alto de uma torre de 40 metros
de altura através da função y = 6t2 – 2. Achar sua
velocidade quando se encontra a 18 metros do solo onde y é
medido em metros e t em segundos.
16) Uma partícula se move segundo a equação
s(t) = t3 – 2t2 + 5t – 1, sendo s medido em metros e t em
segundos. Em que instante a sua velocidade vale 9 m/s?
17) Dois corpos têm movimento em uma mesma reta segundo
as equações s1 = t3 + 4t2 + t – 1 e s2 = 2t3 – 5t2 + t + 2.
Determine as velocidades e posições desses corpos quando
as suas acelerações são iguais.
18) Uma partícula descreve um movimento circular segundo a
equação θ = 2t4 – 3t2 – 4 (θ em radianos). Determine a
velocidade e a aceleração angulares após 4 segundos.
19) Certa imobiliária aluga salas comerciais por R$ 600,00
mensais. Este aluguel sofre um reajuste mensal de 2%.
Calcule a taxa de variação do aluguel daqui a 10 meses.
20) Um cubo de metal com aresta x foi aquecido e dilatou-se
uniformemente.
a) Determine a taxa de variação média do seu volume
quando a aresta aumenta de 3 para 3,01 cm.
b) Determine a taxa de variação do seu volume em relação
à aresta para x = 3 cm.
21) Sabemos que a área A de um quadrado de lado l é: A = l2.
Determinar:
a) a taxa de variação média da área de um quadrado em
relação ao lado quando este varia de 3 a 3,5 metros;
b) a taxa de variação da área em relação ao lado quando
este mede 5 metros.
–
78 –
Introdução ao Cálculo
22) Numa certa fábrica, , o número de peças produzidas nas
primeiras t horas diárias de trabalho é dado pelo gráfico
abaixo:
peças produzidas
Peças produzidas por hora de trabalho
2000
1500
1000
500
0
0
2
4
6
8
10
horas
a) Qual a razão de produção (em unidades por hora) após
3 horas de trabalho? E após 7 horas?
b) Quantas peças são produzidas na oitava hora de
trabalho?
23) Uma caixa d’água está sendo esvaziada para limpeza. A
quantidade de água na caixa, em litros, t horas após o
escoamento ter começado é dada por:
v = 50(80 − t )2
Determinar:
a) A taxa de variação média do volume de água no
reservatório durante as 8 primeiras horas de
escoamento.
b) A taxa de variação do volume de água no reservatório
após 10 horas de escoamento.
–
79 –
Introdução ao Cálculo
c) A quantidade de água que sai do reservatório nas 7
primeiras horas de escoamento.
d) Esboce o gráfico da função e resolva graficamente os
itens a, b e c.
24) Uma chapa metálica quadrada de lado x está se expandindo
segundo a equação x = 2+ t2, onde a variável t representa o
tempo. Determinar a taxa de variação da área desse
quadrado no tempo t = 2.
25) (FLEMMING, página 256, exercício
experimental,
constatou-se
que
desenvolvimento pesa em gramas
1

2
20 + .(t + 4 )
w(t ) = 
2
24,4t + 604
Numa granja
uma
ave
em
5)
, para 0 ≤ t ≤ 60
, para 60 ≤ t ≤ 90,
onde t é medido em dias.
a) Qual a razão do aumento do peso da ave quando t= 50?
b) Quanto a ave aumentará no 51o dia?
c) Qual a razão de aumento de peso quando t=80?
26) Numa pequena comunidade obteve-se uma estimativa que
daqui
a
t
anos
a
população
será
de
5
p (t ) = 20 −
milhares. Daqui a 18 meses, qual será a
t +1
taxa de variação da população desta comunidade?
–
80 –
Introdução ao Cálculo
distância (metros)
27) Um corpo se move em linha reta, de modo que sua posição
no instante t é dada pelo gráfico abaixo, onde o tempo é
dado em segundos e a distância em metros.
210
180
150
120
90
60
30
0
0
2
4
6
8
10
tempo (segundos)
a) Achar a velocidade média durante o intervalo de tempo
[3;4].
b) Achar a velocidade do corpo no instante t = 3.
28) A posição de uma partícula que se move no eixo x depende
do tempo de acordo com o gráfico abaixo, em que x vem
expresso em metros e t em segundos:
10
posição (m)
0
-10 0
1
2
3
4
-20
-30
-40
-50
tempo (s)
a) Qual o seu deslocamento depois de 4 segundos?
–
81 –
5
Introdução ao Cálculo
b) Qual a velocidade da partícula quando t = 4 segundos?
29) Uma piscina está sendo drenada para limpeza. Se o seu
volume inicial de água era de 72.000 litros e depois de um
tempo de t horas este volume diminuiu 2.000t2 litros,
determinar:
a) tempo necessário para o esvaziamento da piscina;
b) taxa média de escoamento no intervalo [3,6];
c) taxa de escoamento depois de 3 horas do início do
processo.
30) A que taxa o nível d’água diminui num tanque cilíndrico de
raio igual a 1 metro se bombearmos o líquido a uma taxa de
-2.000 litros por minuto?
31) (FLEMMING, página 251, exemplo 6) O raio de uma
circunferência cresce à razão de 21cm/s. Qual a taxa de
crescimento do comprimento da circunferência em relação
ao tempo.
32) (FLEMMING, página 257, exercício 13) Um tanque tem a forma
de um cilindro circular reto de 5m de raio de base e 10 m
de altura. No tempo t=0 a água começa a fluir no tanque à
razão de 25m3/h. Com que velocidade o nível de água
sobe?
33) (FLEMMING, página 256, exercício 7) A temperatura de um gás
é mantida constante e sua pressão p em kgf/cm3 e volume v
em cm3 estão relacionadas pela igualdade vp = c, onde c é
constante. Achar a razão de variação do volume em relação
à pressão quando esta vale 10 kgf/cm3.
34) (FLEMMING, página 252, exemplo 7) Um ponto P(x,y) se move
ao longo do gráfico da função y = 1/x. Se a abscissa varia à
razão de 4 unidades por segundo, qual é a taxa de variação
da ordenada quando a abscissa é x = 1/10?
–
82 –
Introdução ao Cálculo
35) (FLEMMING, página 257, exercício 15) Uma usina de britagem
produz pó de pedra, que ao ser depositado no solo, forma
uma pilha cônica onde a altura é aproximadamente igual a
4/3 do raio da base.
a) Determine a razão de variação do volume em relação ao
raio da base.
b) Se o raio da base varia a uma taxa de 20 cm/s, qual a
razão de variação do volume quando o raio mede 2 m?
36) (FLEMMING, página 257, exercício 14) Achar a razão de
variação do volume V de um cubo em relação ao
comprimento de sua diagonal. Se a diagonal está se
expandindo a uma taxa de 2 m/s, qual a razão de variação
do volume quando a diagonal mede 3 m?
37) (FLEMMING, página 258, exercício 17) Um objeto se move sobre
uma parábola y = 2x2 + 3x – 1 de tal modo que sua abscissa
varia à taxa de 6 unidades por minuto. Qual é a taxa de
variação de sua ordenada quando o objeto estiver no ponto
(0,-1)?
Respostas:
1) a) 14 m
b) 27 m
c) 13 m/s
d) 11 m/s
2) a) 1600m
b) 120 m/s
c) 240 m/s
3) a) 4 m/s
b) Gráfico
4) a) 80 m
b) 40 m/s
c) 80 m/s
d) 3 s
–
83 –
Introdução ao Cálculo
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
e) 60 m/s
f) 120 m/s
40 milhões de pessoas/ano
a) 61917 bactérias
b) 1832.1,2t
c) 11288 bactérias/hora
a) 49
b) 75
–8800 l/min; -10400 l/min
50 m/s
1 s e 2,5 s
a) Gráfico
b) Gráfico
c) Gráfico
v = 12t3 – 2 ; a = 36t2
71 m/s; 50 m/s2
18 m/s; 10m/s2
24 m/s
2s
v1 = 52 m/s; v2 = 25 m/s; s1 = 65 m; s2 = 14m
488 rad/s; 378 rad/s2
R$14,48/mês
a) 27,09 cm3/cm
b) 27 cm3/cm
a) 6,5 m2/m
b) 10 m2/m
a) 350 peças/hora
b) 200 peças/hora
c) 200 peças
a) –7600 l/hora
b) –7000 l/hora
c) –53550 l
48
a) 54 g/dia
b) 54,5 g/dia
c) 24,4 g/dia
800 pessoas/ano
a) 23m/s
b) 22 m/s
a) –16 m
b) –24 m/s
–
84 –
Introdução ao Cálculo
29) a) 6 h
b) –18000 l/h
c) –12000 l/h
30) – 0,64 m/min
31) 42π cm/s
32) 0,32 m/h
33) –0,01c cm3/kgf/cm3
34) –400
35) a) 4πr2/3
b) 1,07π m3/s
d2 2
36)
m ; 6 3 m3 / s
3
37) 18 unidades/minuto
–
85 –