1 Quantização não linear

1
Quantização não linear
No caso da quantização linear ou uniforme, teremos erros de quantização relativamente
grandes para sinais de pequeno valor.
• Estes erros poderiam ser de mesma grandeza que o próprio sinal de entrada e a razão
sinal-ruído não seria suficientemente grande para a recuperação da informação.
• Por este motivo usam-se intervalos de quantização de larguras diferentes, caracterizando a quantização não-linear.
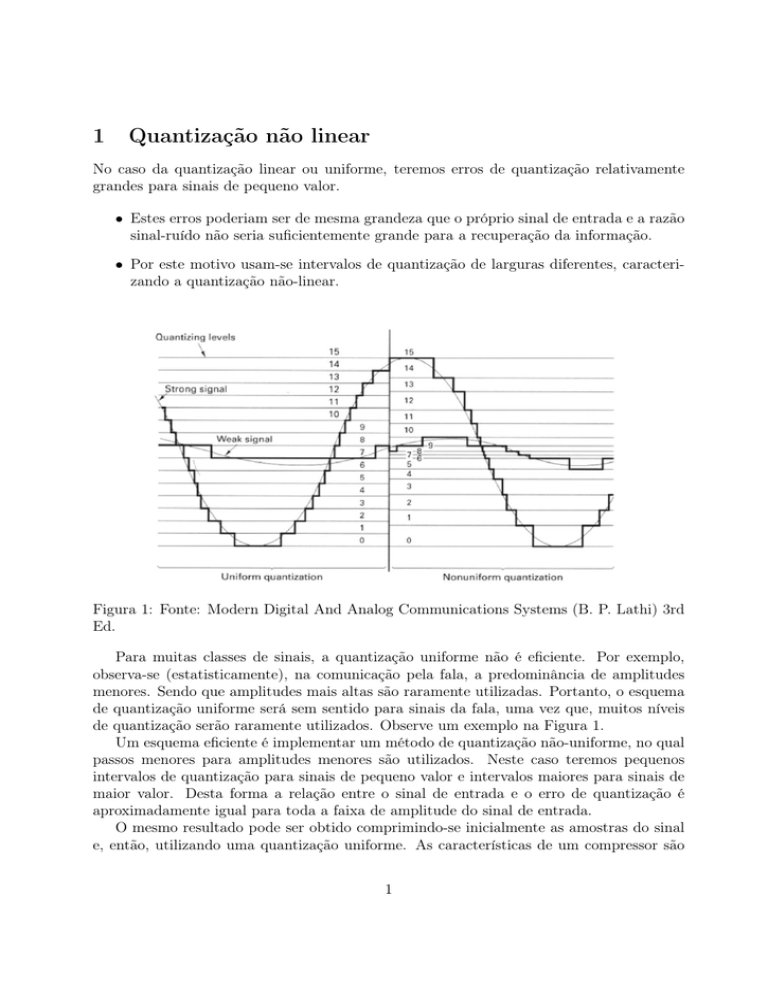
Figura 1: Fonte: Modern Digital And Analog Communications Systems (B. P. Lathi) 3rd
Ed.
Para muitas classes de sinais, a quantização uniforme não é eficiente. Por exemplo,
observa-se (estatisticamente), na comunicação pela fala, a predominância de amplitudes
menores. Sendo que amplitudes mais altas são raramente utilizadas. Portanto, o esquema
de quantização uniforme será sem sentido para sinais da fala, uma vez que, muitos níveis
de quantização serão raramente utilizados. Observe um exemplo na Figura 1.
Um esquema eficiente é implementar um método de quantização não-uniforme, no qual
passos menores para amplitudes menores são utilizados. Neste caso teremos pequenos
intervalos de quantização para sinais de pequeno valor e intervalos maiores para sinais de
maior valor. Desta forma a relação entre o sinal de entrada e o erro de quantização é
aproximadamente igual para toda a faixa de amplitude do sinal de entrada.
O mesmo resultado pode ser obtido comprimindo-se inicialmente as amostras do sinal
e, então, utilizando uma quantização uniforme. As características de um compressor são
1
mostradas na Figura 2 e Figura 3. O eixo horizontal é o sinal de entrada normalizado, ou
seja, o sinal original dividido por seu valor máximo de amplitude.
Figura 2: Lei de compressão “A”.
Figura 3: Lei de compressão “µ”.
No compressor ilustrado na Figura 2 e Figura 3 tem-se que:
• O eixo vertical é o sinal de saída y.
• O compressor faz o mapeamento de um incremento ∆x do sinal de entrada para um
grande incremento ∆y quando o valor do sinal de entrada for pequeno.
• O compressor faz o mapeamento de um incremento ∆x do sinal de entrada para um
pequeno incremento ∆y quando o valor do sinal de entrada for grande.
Desta forma a relação entre o sinal de entrada e o erro de quantização é aproximadamente igual para toda a faixa de amplitude do sinal de entrada.
1.1
Lei A & Lei µ
Os detalhes da quantização não-linear são fixados pela curva característica definida pelo
ITU-T (International Telecommunication Union – Telecommunications). Para Europa é
definida a curva (padrão G711, lei A – Figura 2, para o sistema PCM-30 – Europa),
expressa por:

A|x|

se 0 ≤| x |≤ A1
sgn(x) · { 1+ln A },
y=
,
(1)


1+ln A|x|
1
sgn(x) · { 1+ln A }, se A ≤| x |≤ 1
2
em que, x e y são, respectivamente, o sinal sendo quantizado e o sinal quantizado normalizados, estando seus valores entre −1 e 1. A = 87, 6 e


+1, se x(t) > 0
.
sgn(x) =


−1, se x < 0
A ITU–T definiu a curva para lei µ (padrão G711, lei µ – Figura 3, para o sistema
PCM-24 - América do Norte e no Japão) expressa por:
ln 1 + µ | x |
y = sgn(x) ·
, se 0 ≤| x |≤ 1,
(2)
ln (1 + µ)
µ é uma constante positiva igual a 255 na América do Norte.
Para recuperar as amostras do sinal em seus níveis corretos, um expansor com a característica complementar a do compressor é utilizado no receptor. A combinação da compressão
e expansão é chamada de companding conforme ilustra a Figura 4.
Figura 4: Diagrama de blocos para um sistema de quantização não linear
2
Codificação Modulação Delta
A conversão Delta baseia-se no fato de que para muitos sinais, amostrados com uma
frequência adequada, a variância do sinal diferença é menor que a variância do sinal e,
portanto, terá uma faixa dinâmica menor requerendo um menor número de dígitos por
palavra. Este sinal diferença é codificado com apenas um bit.
A modulação delta tem as seguintes características:
• A entrada analógica é aproximada por uma função degrau.
• Sobe-se ou desce-se um nível (δ) em cada intervalo de amostragem.
• Comportamento binário, ou seja, dois símbolos, 0 e 1.
• Toda vez que o sinal da amostra ficar acima da referência (função degrau) a referência
será incrementada em um nível.
3
Figura 5: Modulação delta
• De outro modo ao sinal de referência será decrementado 1 nível.
• Saída é 1 se o valor da amostra ficar acima da função degrau. Saída é 0 de outro
modo.
• Dois valores importantes: δ e a taxa de amostragem (superior a de Nyquist para se
ter um baixo erro de quantização)
• Para se ter um baixo erro de quantização a frequência de amostragem do codificador
delta deve ser superior a de uma modulação PCM.
A modulação Delta produz dois tipos de distorção, ilustradas na Figura 5: o ruído
de overload (slope overload) característica das zonas de transição brusca do sinal, em que
o passo δ do quantizador não é suficiente para o acompanhar; e o ruído granular ou de
quantização, típico das zonas de silêncio ou de pequena variação do sinal de entrada quando
comparado com o passo δ do quantizador.
4