172
CAPÍTULO 6: IMAGEM
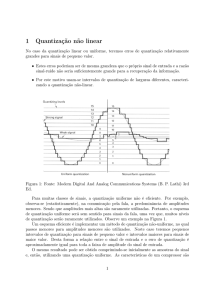
Figura 23. Quantização pelo algoritmo do corte mediano: (A) 256 cores; (B) 16 cores (ver
prancha 6, a cores).
8
Otimização e quantização
O problema de quantização pode ser visto naturalmente como um problema de otimização. Fixado o número de níveis de quantização desejado, existe uma infinidade de
possibilidades entre a escolha das células de quantização e dos níveis de quantização em
cada célula. Uma questão natural é procurar é determinar o particionamento ótimo. Para
isso, devemos tornar preciso o conceito de “ótimo”, definindo uma função objetivo que
deve ser minimizada. Vamos discutir esse problema nesta seção.
8.1
Erro de quantização
Se q é a transformação de quantização e c uma cor a ser quantizada, então
c = q(c) + eq ,
(6.7)
onde o vetor eq é uma medida do erro introduzido no processo de quantização. O erro de
quantização é medido pela distância d(c, q(c)) entre a cor original c e a cor quantizada
q(c).
Diversas métricas d no espaço de cor podem ser escolhidas. com o objetivo de medir
a qualidade do processo de quantização. A escolha dessas métricas deve levar em conta
critérios perceptuais de cor bem como os problemas de eficiência computacional. Na
realidade, basta termos uma função que mede a proximidade de duas cores. Chamamos
a essa função de função distância. Uma função distância bastante utilizada é o quadrado
da distância euclidiana, ou seja, d(c1 , c2 ) = c2 − c1 , c2 − c1 , onde , é um produto
interno no espaço de cor.
Quando estamos quantizando uma imagem, o erro de quantização deve levar em
consideração fatores perceptuais. Um desses fatores é a frequência de ocorrência da cor