forma dessa superfície

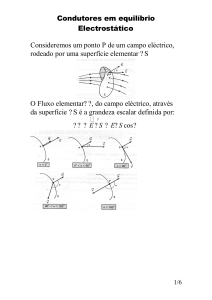
forma dessa superfície. (Pode-se provar que este é o caso porque E  1/ r2) De fato, o
fluxo resultante através de qualquer superfície
q
fechada que envolve uma carga pontual q é dado por
.
0
Figura 6.6. Superfícies fechadas de várias formas englobando uma carga q. O fluxo
eléctrico resultante através de cada superfície é o mesmo.
Considere agora uma carga pontual localizada no exterior de uma superfície
fechada de forma arbitrária, como na Figura 6.7.
Figura 6.7. Carga pontual localizada no exterior de uma superfície fechada. O número
de linhas que entram na superfície é igual ao número de linhas que sai da superfície.
Como se pode ver a partir dessa construção, linhas do campo eléctrico entram
na superfície e linhas do campo saem dela. Entretanto, o número de linhas do campo
eléctrico que entram na superfície é igual ao número que sai da superfície.
Consequentemente, concluímos que é nulo o fluxo eléctrico resultante através de uma
superfície fechada que não engloba nenhuma carga.
Vamos estender esses argumentos para o caso geral de muitas cargas pontuais.
Empregaremos outra vez o princípio de sobreposição. Isto é, podemos expressar o fluxo
resultante através de qualquer superfície fechada como
105
 E  dA   E



1




 E 2  E3 .dA


onde E é o campo eléctrico total em qualquer ponto sobre a superfície, sendo que E1 ,


E 2 e E3 são os campos produzidos pelas cargas individuais nesse ponto. Considere o
sistema de cargas apresentado na Figura 6.8. A superfície S engloba somente uma carga,
q
q1; logo, o fluxo resultante através de S é
. O fluxo através de S devido às cargas
0
exteriores é zero porque cada linha do campo eléctrico dessas cargas que entra em S em
um ponto deixa S em outro ponto. A superfície S’ engloba as cargas q2 e q3; logo, o
q  q2
fluxo resultante através de S' é 1
. Finalmente, o fluxo resultante através da
0
superfície S" é nulo, pois não existe carga alguma dentro dessa superfície. Isto é, todas
as linhas do campo eléctrico que entram em S" num ponto saem de S" em outro ponto.
Figura 6.8. O fluxo eléctrico resultante através de qualquer superfície fechada depende
q
apenas da carga dentro desta superfície. O fluxo resultante através da superfície S é
,
0
q  q2
o fluxo resultante através de S' é 1
, e o fluxo resultante através da superfície S" é
0
zero.
A lei de Gauss, que é uma generalização da discussão anterior, afirma que o
fluxo resultante através de qualquer superfície fechada é
  q
 E   E.dA  int
0
(6.6)

onde o qint representa a carga líquida no interior da superfície e E , o campo eléctrico
em qualquer ponto sobre a superfície. Ou seja, a lei de Gauss afirma que o fluxo
eléctrico resultante através de qualquer superfície fechada é igual à carga líquida dentro
da superfície dividida por 0.
A princípio, a lei de Gauss é válida para o campo eléctrico de qualquer sistema
de cargas ou distribuição contínua de carga. Na prática, entretanto, a técnica é útil para
106
calcular o campo eléctrico somente nas situações onde o grau de simetria é elevado. A
lei de Gauss pode ser usada para calcular o campo eléctrico para as distribuições de
carga que têm simetria esférica, cilíndrica ou plana. Fazemos isso escolhendo uma

superfície gaussiana apropriada, que permita que E seja retirado da integral na lei de
Gauss, e fazendo a integração sobre a área. Observe que uma superfície gaussiana é
uma superfície matemática e não precisa coincidir com nenhuma superfície física real.
6.3. Aplicações da Lei de Gauss
Como foi mencionado anteriormente, a lei de Gauss é útil para determinar campos
eléctricos quando a distribuição de carga tem um elevado grau de simetria. Os exemplos
seguintes mostram maneiras de escolher a superfície gaussiana nas quais a integral de
superfície dada pela equação 6.6 pode ser simplificada, e o campo eléctrico
determinado. A superfície deve sempre ser escolhida para aproveitar a simetria da
distribuição de carga, de maneira que possamos remover E da integral e resolver a
integral. O objectivo nesse tipo de cálculo é determinar uma superfície que satisfaça a
uma ou mais das seguintes condições:
(1) Pode-se afirmar por simetria que o valor do campo eléctrico é constante sob a
superfície.
(2) O produto escalar na equação 6.6 pode ser expresso como um simples


produto algébrico porque E e dA são paralelos.


(3) O produto escalar na equação 6.6 é zero porque E e dA são perpendiculares.
(4) Pode-se afirmar que o campo é zero em qualquer parte da superfície.
______________________________________________________________________
Serão resolvidos na aula teórica:
Exemplo 6.1. Campo eléctrico devido a uma carga pontual.
A partir da lei de Gauss, calcule o campo e1étrico devido a uma carga pontual isolada q.
Exemplo 6.2. Distribuição de carga com simetria esférica.
Uma esfera sólida isolante de raio a tem uma densidade volumétrica de carga uniforme
 e uma carga positiva total Q. Calcule o campo eléctrico num ponto dentro da esfera.
______________________________________________________________________
6.4. Condutores em Equilíbrio Electrostático
Um bom condutor eléctrico, tal como o cobre, contém cargas (electrões) que não estão
presas a nenhum átomo e são livres para se mover dentro do material. Quando nenhum
movimento de carga ocorre dentro do condutor, este está em equilíbrio electrostático.
Nessa situação, toda carga no condutor é uma partícula em equilíbrio, sob a acção de
uma força resultante nula. Como veremos, um condutor isolado (um condutor que esteja
isolado da terra) em equilíbrio electrostático tem as seguintes propriedades:
1. O campo eléctrico é nulo em qualquer ponto dentro do condutor.
2. Se o condutor isolado tiver uma carga líquida, a carga em excesso fica
inteiramente sobre sua superfície.
107
3. O campo eléctrico imediatamente exterior ao condutor carregado é
perpendicular à superfície do condutor e tem uma magnitude  / 0, onde  é a
carga por unidade de área nesse ponto.
4. Num condutor de forma irregular, a carga por unidade de área é máxima nos
locais onde é mínimo o raio de curvatura da superfície.
Verificaremos na discussão a seguir as primeiras três propriedades. A quarta
propriedade é apresentada aqui de modo que tenhamos uma lista completa das
propriedades dos condutores em equilíbrio electrostático. Contudo, sua verificação
requer conceitos que veremos mais adiante, de modo que adiaremos sua verificação até
lá.
A primeira propriedade pode ser compreendida considerando-se uma placa condutora

colocada num campo externo E (Figura 6.9). O campo eléctrico dentro do condutor
tem de ser nulo supondo-se que temos equilíbrio electrostático.

Figura 6.9. Placa condutora num campo eléctrico externo E . As cargas induzidas
sobre as superfícies da placa produzem um campo eléctrico que se
opõe ao campo externo, fornecendo um campo resultante nulo dentro do
Se o campo não fosse nulo, cargas livres no condutor seriam aceleradas sob acção da
força eléctrica. Esse movimento dos electrões, entretanto, significaria que o condutor
não está em equilíbrio electrostático. Assim, a existência do equilíbrio electrostático é
consistente somente com um campo nulo no condutor.
Vamos investigar como esse campo nulo é atingido. Antes que o campo externo
seja aplicado, os electrões livres estão distribuídos uniformemente por todo condutor.
Quando o campo externo é aplicado, os electrões livres aceleram para esquerda na
Figura 6.9, fazendo que um plano da carga negativa esteja presente na superfície
esquerda. O movimento dos electrões para a esquerda resulta num plano de carga
positiva na superfície direita. Esses planos de carga criam um campo eléctrico adicional
dentro do condutor que se opõe ao campo externo. Quando os electrões se movem, a
carga por unidade de superfície aumenta até que a magnitude do campo interno se
iguale à magnitude do campo externo, fornecendo um campo resultante nulo dentro do
condutor.
Podemos usar a lei de Gauss para verificar a segunda propriedade de um
condutor em equilíbrio electrostático. A Figura 6.10 mostra um condutor com uma
forma arbitrária. Uma superfície gaussiana é desenhada dentro do condutor e pode ser
tão próxima da superfície quanto desejarmos. Como acabamos de mostrar, o campo
eléctrico em toda parte de dentro de um condutor em equilíbrio electrostático é nulo.
Consequentemente, o campo eléctrico tem de ser nulo em todo ponto sobre a superfície
gaussiana. A partir
108
  q
desse resultado e da lei de Gauss,  E   E.dA  int , concluímos que é nula a carga
0
líquida dentro da superfície gaussiana. Como não pode haver nenhuma carga resultante
dentro da superfície gaussiana (que é arbitrariamente próxima da superfície do
condutor), qualquer carga líquida no condutor tem de estar em sua superfície. A lei de
Gauss não nos diz como esse excesso de carga é distribuído na superfície, apenas que
ele tem de estar na superfície.
Figura 6.10. Um condutor isolado de forma arbitrária. A linha tracejada
representa uma superfície gaussiana junto da face interna da superfície física do
condutor.
Conceptualmente, podemos compreender a posição das cargas na superfície
imaginando muitas cargas colocadas no centro do condutor. A repulsão mútua das
cargas faz com que se afastem. Elas se afastarão o quanto puderem, movendo-se para a
superfície.
Figura 6.11. Uma superfície gaussiana na forma de um cilindro pequeno é usada para
calcular o campo eléctrico junto da face externa de um condutor carregado. O fluxo
através da superfície gaussiana é EnA.
Para verificar a terceira propriedade, também podemos usar a lei de Gauss.
Desenhamos uma superfície gaussiana na forma de um cilindro pequeno que tem suas
bases paralelas à superfície (Figura 6.11). Parte do cilindro está fora do condutor e parte
está dentro. O campo é normal à superfície porque o condutor está em equilíbrio

electrostático: se E tivesse uma componente paralela à superfície, uma força eléctrica
paralela à superfície seria exercida sobre as cargas, as cargas livre mover-se-iam ao
longo da superfície e, assim, o condutor não estaria equilíbrio; nenhum fluxo atravessa
109

esta parte (do cilindro) da superfície gaussiana porque E é paralelo a esta parte da
superfície. Nenhum fluxo atravessa a face plana do cilindro dentro do condutor porque

E = 0. Logo, o fluxo resultante através da superfície gaussiana é o fluxo através da face
plana fora do condutor onde o campo é perpendicular à superfície. Para essa face, o
fluxo é EA, onde E é o campo eléctrico na face externa do condutor e A é a área da face
do cilindro. A aplicação da lei de Gauss à essa superfície fornece
 E   EdA  EA 
qint
0

A
0
Assim E será
E

0
(6.7)
Na Figura 6.12 vemos o padrão do campo eléctrico de uma placa condutora carregada
próxima de um cilindro condutor com carga oposta.
Figura 6.12. Padrão do campo eléctrico de uma placa condutora carregada próxima de
um cilindro condutor com carga oposta. Pequenos pedaços de fibra suspensos em óleo
se alinham com as linhas do campo eléctrico. Observe que (1) as linhas do campo
eléctrico são perpendiculares aos condutores e (2) não há linhas dentro do cilindro
(E= 0).
110