Dinâmica dos Fluidos - Instituto de Física / UFRJ

IF/UFRJ
Física II – 2010/2
a
2 Lista de Problemas – Dinâmica dos Fluidos
1. [RHK4-18.2] A mangueira de um jardim tem 1,9 cm de diâmetro interno e está
ligada a um irrigador que consiste em um recipiente cilíndrico com 24 furos, cada
um deles com 0,12 cm de diâmetro. Se no interior da mangueira a velocidade da
água é 1,05 m/s, com que velocidade ela deixa os orifícios do irrigador?
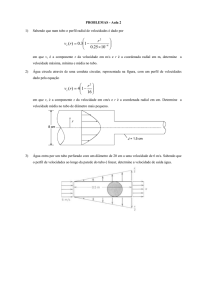
2. [RHK4-18.3] A figura mostra a confluência de dois
cursos d’água para formar um rio. Um dos cursos
tem 8,2 m de largura, 3,4 m de profundidade e uma
corrente d’água com velocidade 2,3 m/s. O outro
curso tem 6,8 m de largura, 3,2 m de profundidade
e escoa a 2,6 m/s. A largura do rio é de 10,7 m e a
velocidade da água é de 2,9 m/s. Qual a sua
profundidade?
3. [RHK4-18.9] Algumas vezes são realizados testes com modelos de torpedos
colocados no interior de uma tubulação horizontal por onde escoa água, da mesma
maneira que um túnel de vento é usado para testar modelos de aviões. Considere
uma tubulação circular de diâmetro interno de 25,5 cm e um modelo de torpedo com
4,80 cm de diâmetro alinhado com o eixo da tubulação. Queremos testar o torpedo
com a água escoando em torno dele a 2,76 m/s. (a) Qual deve ser a velocidade da
água em pontos no interior da tubulação bem distantes do torpedo? (b) Ache a
diferença de pressão entre estes pontos e pontos próximos à superfície lateral do
torpedo.
4. [RHK4-18.13] As janelas de um edifício medem 4,26 m por 5,26 m. Num dia de
tempestade, o vento está soprando a 28,0 m/s paralelamente a uma janela do 53.o
andar. Calcule a força resultante sobre a janela. A densidade do ar é de 1,23 kg/m3.
5. [RHK4-18.16] Um tanque contém água até a altura H. É feito um pequeno orifício
na sua parede, à profundidade h abaixo da superfície
da água (figura). (a) Mostre que a distância x da base
da parede até onde o jato atinge o solo é dada por
. (b) Poderia ser perfurado um orifício
a outra profundidade, de modo que este segundo jato
tivesse o mesmo alcance? Em caso afirmativo, a que
profundidade? (c) Determinar a que profundidade h
deveria ser feito um pequeno orifício para que a água
que sair por ele atinja o solo à distância máxima da
base. Qual é esta distância máxima?
6. [RHK4-18.17] Uma pessoa atira em um tanque contendo
gasolina, fazendo um furo na parede do tanque 53,0 m abaixo
da superfície da gasolina. O tanque estava selado e com uma
pressão igual a 3,10 atm (absoluta), como vemos na figura. A
densidade da gasolina no interior do tanque é de 660 kg/m3.
Com que velocidade a gasolina começa a escoar pelo furo?
7. [RHK4-18.19] Uma pessoa sopra ar com velocidade de 15
m/s, através de um dos ramos de um tubo em U que contém
água. Qual será a diferença entre os níveis da água? Considere a densidade do ar
igual 1,2 kg/m3.
8. [RHK4-18.20] A água represada por um dique tem 15,2 m de profundidade. Um
cano horizontal de 4,30 cm de diâmetro passa
através do dique 6,15m abaixo da superfície da
água, como ilustra a figura. A extremidade do
cano no lado seco do dique está tampada. (a)
Calcule a força de atrito entre a parede do cano e a
tampa. (b) A tampa é removida. Qual o volume de
água que escoa pelo cano em 3 horas?
9. [HMN-2.3] Um reservatório contém água até 0,5 m de altura e, sobre a água, uma
camada de óleo, de densidade 0,69 g/cm3, também de 0,5 m de altura. Abre-se um
pequeno orifício na base do reservatório. Qual é a velocidade de escoamento da
água?
10. [RHK4-18.21] Um sifão é um dispositivo para remover
líquidos de um recipiente que não pode ser tombado. Ele
funciona como mostra a figura. O tubo deve ser
inicialmente cheio, mas tão logo isto tenha sido feito, o
líquido escoará até que seu nível paire abaixo da abertura
do tubo em A. O líquido tem densidade ρ e viscosidade
desprezível. (a) Com que velocidade o líquido sai do tubo
em C? (b) Qual é a pressão no líquido no ponto máximo
B? (c) Qual é a maior altura possível h1 a que um sifão
pode fazer subir a água?
11. [RHK4-18.22] (a) Consideremos um fluido de massa específica ρ, que escoa com
velocidade v1 e passa abruptamente de um conduto cilíndrico de área transversal a1,
para outro conduto de maior diâmetro e
área transversal a2; veja a figura. O jato de
líquido que emerge do conduto estreito
mistura-se com o que se encontra na
canalização maior, depois ele escoa quase
uniformemente com velocidade média v2.
Sem preocupar-se com os pormenores,
aplique o conceito de momento linear para
mostrar que o aumento de pressão devido à mistura é aproximadamente igual a
. (b) Demonstre, partindo da equação de Bernouilli, que em
um conduto cuja seção aumentasse gradualmente, a diferença seria
. (c) Explique a perda de pressão devida ao alargamento
brusco do conduto. Você pode fazer uma analogia com os choques elásticos e
inelásticos na mecânica da partícula?
12. [RHK4-18.23] Um recipiente contém suco de laranja suficiente para encher 15
copos. Quando a torneira no fundo do recipiente é aberta, são necessários 12,0 s
para encher um copo. Se deixarmos a torneira aberta, quanto tempo será necessário
para encher os 14 copos restantes?
13. Um tanque aberto de seção reta constante, A, é alimentado por um cano que despeja
uma vazão (volume por unidade de tempo) R0. A água
sai do tanque por um orifício de área a, junto à sua base.
(a) Determine a velocidade com que a água sai pelo
orifício, em função da aceleração da gravidade g, da
altura h da superfície livre da água (medida a partir do
orifício), e das áreas A e a. (b) Calcule em que altura, h0,
se estabelece o nível de água no tanque em regime
permanente.
14. [RHK4-18.25] Um tubo oco está colado, em uma das extremidades, a um disco DD
(figura). O conjunto é colocado um pouco acima de um outro
disco CC de papelão. Soprando-se pelo tubo, o disco CC é
atraído para DD. Seja A a área do papelão e v a velocidade
média do ar entre CC e DD. Determinar a força dirigida para
cima que atua no papelão, cujo peso deve ser desprezado.
Suponha que v0 << v, onde v0 é a velocidade do ar no interior do
tubo.
15. [RHK4-18.27 + HMN-2.14] O ar escoa sobre a parte superior da asa de um avião,
cuja área é A, com velocidade vs, e sob a parte inferior da asa com velocidade vi. (a)
Mostre que a equação de Bernouilli prevê que a força de sustentação S, orientada
para cima sobre a asa será
, onde ρ é a densidade do ar. (Sugestão:
Aplique a equação de Bernouilli a uma linha de corrente bem próxima à superfície
superior da asa e a outra linha de corrente igualmente próxima à superfície inferior.
Você pode justificar o fato de termos considerado iguais as constantes para as duas
linhas de corrente?). (b) Suponha que a massa do avião seja 2.000 kg, que a área
total coberta pela asa seja de 30 m2, e que o desenho da asa seja tal que a velocidade
de escoamento na parte superior seja 25% superior à velocidade na parte inferior;
tomando a densidade da atmosfera como 1,3 kg/m3, estime a velocidade de
escoamento mínima, na parte superior, necessária para o avião decolar.
16. [RHK4-18.29] Suponha que, ao deslocar-se em volta de uma asa de avião, o ar
esteja estagnado em sua borda dianteira e que em sua face superior a velocidade seja
v. Considere a pressão na borda dianteira aproximadamente igual à atmosférica e
determine o maior valor possível para v, admitindo o escoamento estacionário e o ar
incompressível; utilize a equação de Bernouilli. A densidade do ar é de 1,2 kg/m3.
Compare a velocidade obtida no item anterior com a velocidade do som no ar, de
340 m/s. Explique a diferença. Deveria haver alguma relação entre as duas
velocidades?
17. [RHK4-18.41] Um fluido de viscosidade η escoa em regime estacionário através de
um tubo horizontal cilíndrico de raio R e
comprimento L, como mostrado na figura.
(a) Considere um cilindro de fluido
arbitrário, de raio r. Mostre que a força
viscosa F devida à camada vizinha é
. (b) Mostre que a força F’
que empurra o fluido através do tubo é
. (c) Use a condição de
equilíbrio para obter uma expressão para dv em termos de dr. Integre esta expressão
para obter
.
18. [RHK4-18.42] Considere novamente o fluido escoando através do tubo descrito no
problema anterior, e ilustrado na figura. Ache uma expressão para o fluxo de massa
através do anel definido pelos raios r e r + dr; integre este resultado para obter o
fluxo de massa total através do tubo,
.
19. [HMN-2.13] Petróleo de densidade 0,85 g/cm3 e viscosidade 1 poise é injetado , à
pressão de 5 atm numa extremidade de um oleoduto de 20 cm de diâmetro e 50 km
de comprimento, emergindo na outra extremidade à pressão atmosférica. (a) Calcule
a vazão em litros/dia. (b) Calcule a velocidade de escoamento ao longo do eixo do
oleoduto.
Respostas:
2) 3,9 m.
3) (a) 2,66 m/s; (b) 271 Pa.
4) 10,8 kN
6) 41,0 m/s
7) 1,38 cm
8) (a) 73,9 N; (b) 147 m3.
9) 3,96 m/s.
10) (a)
; (b)
12) 5 min 42 s.
13) (a)
14)
; (b)
.
15) 190 km/h.
16) 410 m/s.
19) (a) 2,75 litros/dia; (b) 0,203 m/s.
; (c) 10,3 m.