caderno de exercícios 2b

CADERNO DE EXERCÍCIOS 2B
Ensino Médio – Ciências da Natureza I
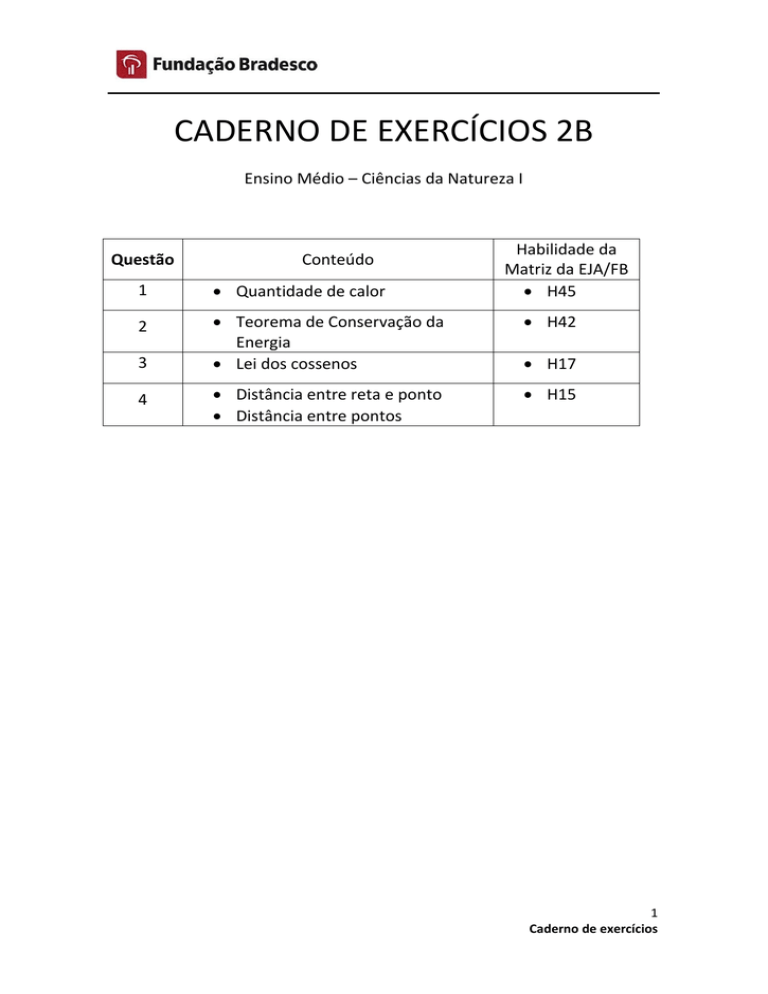
Questão
1
2
3
4
Conteúdo
 Quantidade de calor
Habilidade da
Matriz da EJA/FB
 H45
 Teorema de Conservação da
Energia
 Lei dos cossenos
 H42
 Distância entre reta e ponto
 Distância entre pontos
 H15
 H17
1
Caderno de exercícios
1. (UFPEL) No nordeste do Brasil, as condições de insolação favorecem o uso do fogão solar,
cujo funcionamento é baseado na concentração de energia por meios de espelhos. A água
absorve 2 x 104 calorias por minuto quando aquecida num determinado tipo de fogão solar.
Determine o tempo necessário para aquecer 4 kg de água de 30 ºC a 80 ºC. Considere o
calor específico da água igual a 1 cal/gºC.
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
2
Caderno de exercícios
2. Um skatista parte da posição A situada a 7,2 m do solo. Em seu percurso ele passa pelas
posições B e C (localizadas no solo) e chega à posição D com velocidade de 6 m/s.
A
D
B
7,2 m
v = 6 m/s
C
h
Na situação apresentada admita que ocorre a conservação da energia. Com essas informações
determine:
a)
b)
c)
d)
e)
f)
g)
h)
i)
A energia potencial gravitacional, em relação ao solo, do skatista na posição A.
A velocidade do skatista na posição A.
A velocidade do skatista na posição B. Expresse esse valor em km/h.
A energia potencial gravitacional, em relação ao solo, do skatista na posição C.
A velocidade do skatista na posição C.
A altura atingida pelo skatista na posição D.
A energia cinética do skatista na posição D.
A energia potencial gravitacional, em relação ao solo, do skatista na posição D
A energia mecânica do skatista na posição D.
Informações adicionais:
Massa do sistema skate – skatista = 62 kg
Aceleração da gravidade: 10 m/s2
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
3
Caderno de exercícios
3. No ponto turístico de uma cidade deseja-se construir uma tirolesa. Para tanto, é necessário
saber qual é a distância do alto da rocha até o mar, para que se possa providenciar o cabo
de aço que será utilizado para o deslocamento dos praticantes de tirolesa. Observe a
ilustração que apresenta esta situação e, com as informações fornecidas, calcule qual
deverá ser o comprimento do cabo de aço. A tirolesa deverá se deslocar do ponto A (alto
rocha) até ponto B (mar).
A tirolesa é uma atividade esportiva de
aventura originária da região do Tirol, na
Áustria. Consiste em um cabo aéreo
ancorado entre dois pontos, pelo qual o
praticante se desloca através de roldanas.
A
20 m
120°
B
C
15 m
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
4
Caderno de exercícios
4. No plano cartesiano apresentado, temos um triângulo. Deseja-se saber qual é a área deste
triângulo. Para auxiliar neste cálculo temos as seguintes informações:
Reta d: – x + 2y = 0
Coordenadas dos pontos: A ( 2,1), B( 4,4) e C( 6,3)
Para calcular a área do triângulo utilizamos a expressão área = base x altura
2
Para encontrar o valor da altura é necessário calcular a distância entre o ponto B e a reta d.
Para encontrar o valor da base é necessário calcular a distância entre os pontos A e C.
altura
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
5
Caderno de exercícios
GABARITO COMENTADO
1. Inicialmente determinamos a quantidade de calor necessária para elevar a agua a uma
temperatura de 30 oC para a temperatura de 80 oC. Utilizando a expressão
Q = m.c. 
Q = quantidade de calor a ser determinada
m = massa de agua = 4 kg = 4.000 g
c = calor específico da água, cujo valor foi enunciado do exercício vale 1 cal/g oC.
 = variação da temperatura = 80 oC – 30 oC = 50 oC
Substituindo esses valores na expressão teremos:
Q = m.c. 
Q = 4.000 x 1 x 50
Q = 200.000 cal
Esse valor significa que a água precisa receber 200.000 calorias para elevar sua temperatura de
30 oC para 80 oC.
Entretanto o exercício solicita que determinemos o tempo (t) necessário para chegar na
temperatura de 80 oC.
Pela informação do enunciado a água absorve 2 x 104 calorias por minuto.
Lembre-se que o valor 2 x 104 está escrito em notação científica e também pode ser reescrito
da seguinte forma:
2 x 104 = 20.000 calorias.
Ou seja, em 1 minuto a água recebe, de acordo com o enunciado do exercício, 20.000 calorias.
Então, utilizando a relação de proporcionalidade, podemos determinar quanto tempo será
necessário para absorver 200.000 calorias.
“Multiplicando em cruz” ficamos com a seguinte relação:
1 minuto
20.000 calorias
t minutos
200.000 calorias
20.000t = 200.000
6
Caderno de exercícios
t = 200.000
20.000
t = 10 minutos
Esse valor indica o tempo necessário para a água subir sua temperatura de 30 oC para 80 oC.
2.
a) A energia potencial gravitacional, em relação ao solo, do skatista na posição A.
Utilizando a expressão Ep = m.g.h onde:
m = 62 kg
g = 10 m/s2
h = altura na posição A = 7,2 m
teremos:
Ep = m.g.h
Ep = 62.10.7,2
Ep = 4.464 J
b) A velocidade do skatista na posição A.
O skatista inicia seu movimento na posição A. Considerando que ele estava parado sua
velocidade nessa posição é nula ( v = 0).
c) A velocidade do skatista na posição B.
De acordo com o enunciado ocorre conservação da energia. Portanto teremos que:
Energia mecânica na posição A = Energia mecânica na posição B
ou seja,
(Emecânica)A = (Emecânica)B
E lembrando que a energia mecânica é a soma da energia potencial gravitacional com a
energia cinética teremos, pelo Teorema de Conservação da Energia:
Energia potencial
+
Energia cinética
=
na posição A
(EP + EC)A
Energia potencial
+
Energia cinética
na posição B
=
(EP + EC)B
e lembrando das expressões para a energia potencial gravitacional (Ep) e energia cinética (Ec):
7
Caderno de exercícios
Ep = m.g.h
Ec = m.v2
2
Teremos
(EP + EC)A
(m.g.h + m.v2)A
2
=
(EP + EC)B
=
(m.g.h + m.v2)B
2
Observado os valores em cada uma das posições teremos:
Posição A
m = 62 kg
g = 10 m/s2
h =7,2 m
v=0
Posição B
m = 62 kg
g = 10 m/s2
h =0
v = valor a ser determinado
Substituindo esses valores na expressão acima:
(m.g.h + m.v2)A = (m.g.h + m.v2)B
2
2
62.10.7,2 + 62.(02) = 62.10.0 + 62.v2
2
2
4.464 + 0 = 0 + 31.v2
4.464 = 31.v2
4.464 = v2
31
144 = v2
v2 = 144
Extraindo a raiz quadrada de 144 encontramos o valor 12. Portanto v = 12 m/s. Ou seja, a
velocidade do skatista no solo (ponto B) é de 12 m/s.
8
Caderno de exercícios
Para escrevermos essa velocidade em km/h lembremos da relação:
1 m/s = 3,6 km/h
Logo 12 m/s = 12 x 3,6 = 43,2 km/h.
d) A energia potencial gravitacional do skatista, em relação ao solo, na posição C.
Assim como na posição B, o skatista está a uma altura nula ( h = 0), com relação ao solo, na
posição C.
Considerando que a energia potencial gravitacional é diretamente proporcional à altura, nessa
posição ela também será nula pois
Ep = m.g.h onde m = 62 kg, g = 10 m/s2 e h = 0.
Ep = m.g.h
Ep = 62.10.0
Ep = 0
e) A velocidade do skatista na posição C.
Admitindo que se mantém a conservação da energia não havendo perdas entre as posições B e
C a velocidade do skatista é a mesma que na posição B. Esse valor para a velocidade foi
determinado no item c).
Velocidade na posição B = Velocidade na posição C = 12 m/s (43,2 km/h)
f) A altura atingida pelo skatista na posição D.
Novamente, de acordo com o enunciado, ocorre conservação da energia. Portanto teremos
que:
Energia mecânica na posição C = Energia mecânica na posição D
Ou seja
(Emecânica)C = (Emecânica)D
E lembrando que a energia mecânica é a soma da energia potencial gravitacional com a
energia cinética teremos, pelo Teorema de Conservação da Energia:
Energia potencial
+
Energia cinética
=
na posição C
(EP + EC)C
Energia potencial
+
Energia cinética
na posição D
=
(EP + EC)DD
9
Caderno de exercícios
e lembrando das expressões para a energia potencial gravitacional (Ep) e energia cinética (Ec):
Ep = m.g.h
Ec = m.v2
2
Teremos
(EP + EC)C
(m.g.h + m.v2)C
2
=
(EP + EC)D
=
(m.g.h + m.v2)D
2
Observado os valores em cada uma das posições, teremos:
Posição C
m = 62 kg
g = 10 m/s2
h=0
v = 12 m/s
Posição D
m = 62 kg
g = 10 m/s2
h = valor a ser determinado
v = 6 m/s
Substituindo esses valores na expressão acima:
(m.g.h + m.v2)C = (m.g.h + m.v2)D
2
2
62.10.0 + 62.(122) = 62.10.h + 62.(6)2
2
2
0 + 4.464 = 620.h + 1.116
4.464 = 620.h + 1.116
4.464 – 1.116 = 620.h
3.348 = 620.h
3.348 = h
620
h = 5,4 m
Portanto a posição D está localizada a uma altura de 5,4 m.
10
Caderno de exercícios
g) A energia cinética do skatista na posição D
Para determinar a energia cinética na posição D, utilizamos a expressão:
EC = m.v2
2
Onde
m = 62 kg
v = velocidade no posição D = 6 m/s
Teremos:
EC = m.v2
2
EC = 62.(6)2
2
EC = 62x36
2
EC = 2.232
2
EC = 1.116 J
h) A energia potencial gravitacional, em relação ao solo, do skatista na posição D
Para determinar a energia potencial gravitacional na posição D, utilizamos a expressão:
EP = m.g.h
Onde
m = 62 kg
h = altura na posição D em relação ao solo = 5,4 (valor que determinamos no item “f” dessa
questão.
EP = m.g.h
EP = 62.10.5,4
EP = 3.348 J
11
Caderno de exercícios
i) A energia mecânica do skatista na posição D.
A energia mecânica na posição D é dada pela soma das energias cinética e potencial
gravitacional na posição D.
(EMECÂNICA)D = (ECINÉTICA)D + (EPOTENCIAL)D
A energia cinética foi determinada no item “g” e vale 1.116 J.
A energia potencial gravitacional foi determinada no item “h” e vale 3.348 J.
Portanto
(EMECÂNICA)D = (ECINÉTICA)D + (EPOTENCIAL)D
(EMECÂNICA)D = 1.116 + 3.348
(EMECÂNICA)D = 4.464 J
3.
Observamos na ilustração, apresentada na situação-problema, que com as informações
fornecidas, é possível formar um triângulo em que são conhecidos dois lados e um ângulo.
Deseja-se então saber valor do terceiro lado desse triângulo. Para resolver esta situação vamos
aplicar a Lei dos cossenos.
Identificaremos os lados do triângulo da seguinte maneira:
a = 15 m
b = 20 m
c=?
c² = a² + b² - 2.a.b. cos ĉ .
c² = 15² + 20² - 2.15.20.cos120
observação: utilize o valor de – 0,5 para o cos 120.
c² = 225 + 400 – 2.15.20.( -0,5)
c² = 625 – 600.(-,05)
c² = 625 + 300
c² = 925
c=
925
12
Caderno de exercícios
c

30,42
Concluímos que o cabo de aço deverá ter aproximadamente 30,42 metros.
4.
Calculando a distância entre a reta – x + 2y = 0 e o ponto (4,4), medida que representa a altura
do triângulo.
d=
ax0  by0  c
a ²  b²
 1.4  2.4  0
d=
d=
d=
d=
(1)²  (2)²
48
1 4
4
5
4
5
=
5
Utilize o valor de 2,23 para
d = 1,79 (aproximadamente)
5
Observação: como
é um número irracional utilizamos um valor aproximado.
Concluímos que a altura do triângulo mede aproximadamente 1,79.
Calcularemos agora a distância entre os pontos A (2,1) e C (6,3)
AB =
x
AB =
6  2   3  1 
AB =
4   2 
2

 x1
2

 y2  y1
2
2

2
2
2
13
Caderno de exercícios
AB =
16  4
AB =
20
AB
 4,47
Concluímos que a base do triângulo mede aproximadamente 4,47.
Agora que já temos o valor da base do triângulo e da altura, vamos calcular a área desta figura.
área = base x altura
2
área = 4,47 x 1,79
2
área =
8
2
área = 4 unidades ao quadrado (como a unidade de medida não foi definida mencionamos
simplesmente unidades ao quadrado).
14
Caderno de exercícios