Física - Mecânica Clássica

www.fisicaexe.com.br
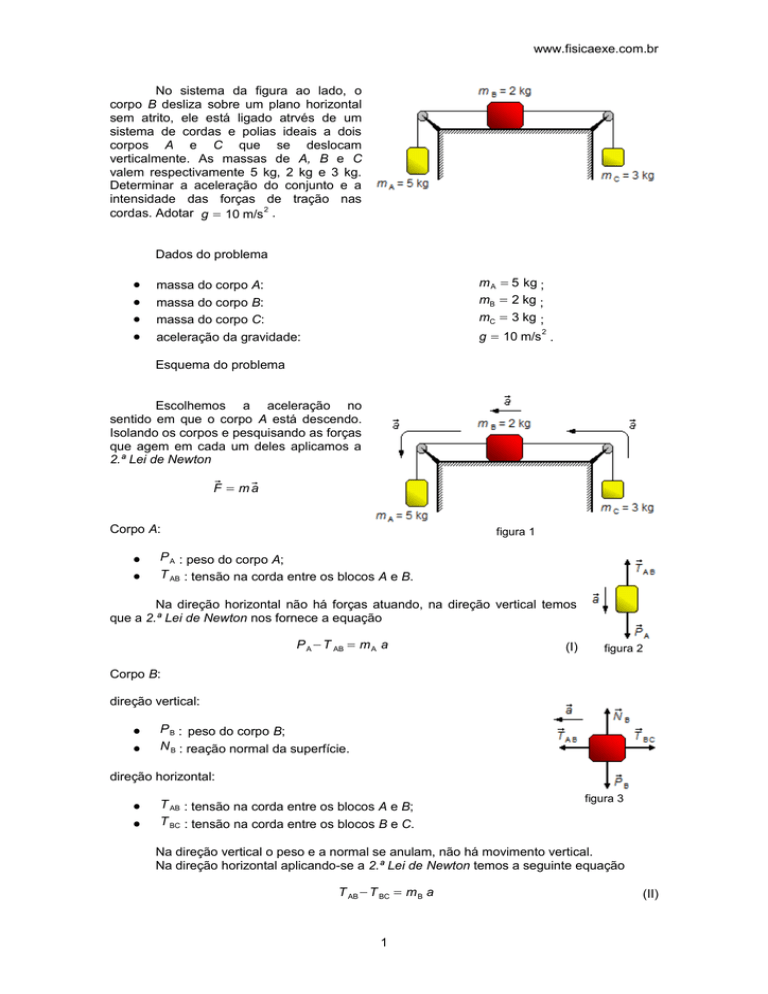
No sistema da figura ao lado, o
corpo B desliza sobre um plano horizontal
sem atrito, ele está ligado atrvés de um
sistema de cordas e polias ideais a dois
corpos A e C que se deslocam
verticalmente. As massas de A, B e C
valem respectivamente 5 kg, 2 kg e 3 kg.
Determinar a aceleração do conjunto e a
intensidade das forças de tração nas
cordas. Adotar g = 10 m/s 2 .
Dados do problema




m A = 5 kg ;
mB = 2 kg ;
mC = 3 kg ;
massa do corpo A:
massa do corpo B:
massa do corpo C:
aceleração da gravidade:
2
g = 10 m/s .
Esquema do problema
Escolhemos a aceleração no
sentido em que o corpo A está descendo.
Isolando os corpos e pesquisando as forças
que agem em cada um deles aplicamos a
2.ª Lei de Newton
 = m
F
a
Corpo A:


figura 1
P A : peso do corpo A;
T AB : tensão na corda entre os blocos A e B.
Na direção horizontal não há forças atuando, na direção vertical temos
que a 2.ª Lei de Newton nos fornece a equação
P A −T AB = m A a
(I)
figura 2
Corpo B:
direção vertical:


P B : peso do corpo B;
N B : reação normal da superfície.
direção horizontal:


T AB : tensão na corda entre os blocos A e B;
T BC : tensão na corda entre os blocos B e C.
figura 3
Na direção vertical o peso e a normal se anulam, não há movimento vertical.
Na direção horizontal aplicando-se a 2.ª Lei de Newton temos a seguinte equação
T AB−T BC = m B a
1
(II)
www.fisicaexe.com.br
Corpo C:


P C : peso do corpo C;
T BC : tensão na corda entre os blocos B e C.
Na direção horizontal não há forças atuando, na direção vertical temos
que a 2.ª Lei de Newton nos fornece a equação
T BC−P C = m C a
(III)
figura 4
Solução
Com as equações (I), (II) e (III) acima temos um sistema de três equações a três
incógnitas (TAB, TBC e a), somando as três equações temos
∣
P A −T AB = m A a
T AB −T BC = m B a
T BC −P C = m C a
P A −PC = (m A +m B+m C) a
P A −P C
a=
m A +m B+m C
(IV)
O módulo das forças peso dos corpos A e C são dadas por
PA = mA g
e
PC = mC g
(V)
substituindo (V) em (IV) e os valores dados no problema
m A g −mC g
m A mB mC
5 . 10−3 .10
a=
523
50−30
a=
10
20
a=
10
a=
a = 2 m/ s
2
Substituindo a massa do corpo A, a expressão para o peso de A dada em (V) e a
aceleração, encontrada acima, na primeira expressão do sistema, a tensão na corda vale
m A g −T AB = mA a
5 . 10−T AB = 5 .2
50−T AB = 10
T AB = 50−10
T AB = 40 N
Substituindo a massa do corpo C, a expressão para o peso de C dada em (V) e a
aceleração, encontrada acima, na terceira expressão do sistema, a tensão na corda vale
T BC− mC g = m C a
T BC −3.10 = 3 .2
T BC −30 = 6
2
www.fisicaexe.com.br
T BC = 630
T AB = 36 N
3