Slide 1 - Educacional

Cinemática
Mecânica
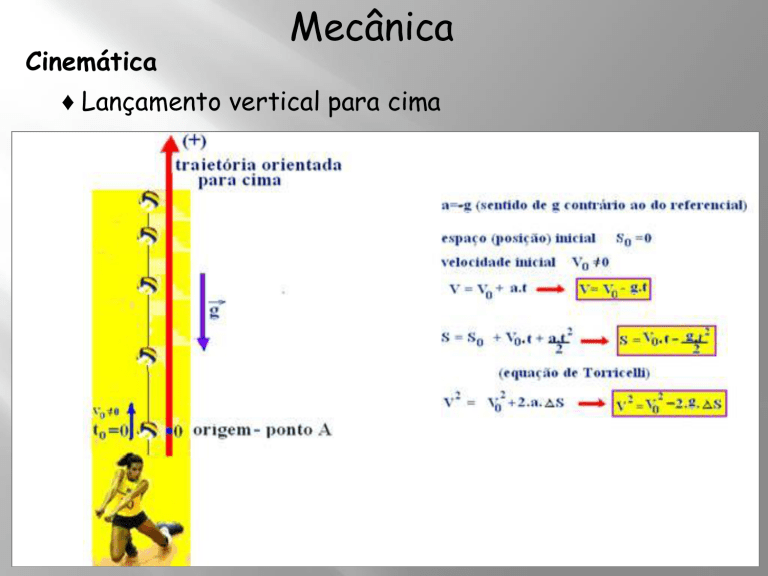
♦ Lançamento vertical para cima
O que você deve saber
● Na subida, o movimento é progressivo, pois o deslocamento ocorre no
sentido crescente da trajetória, e retardado, pois o módulo da
velocidade está diminuindo.
● Na descida, o movimento é retrogrado, pois o deslocamento ocorre no
sentido decrescente da trajetória, e acelerado, pois o módulo da
velocidade está aumentando.
● No ponto mais alto da trajetória, a velocidade se anula (V = 0), pois é o
ponto em que o corpo inverte o sentido de seu movimento e nesse ponto a
altura atingida pelo corpo é máxima.
● O tempo de subida é igual ao tempo de descida.
● A velocidade (Vo) de lançamento na origem é igual à mesma velocidade
de chegada à origem, mas de sinal contrário (-Vo).
● Em qualquer ponto da trajetória o corpo tem duas velocidades de
mesmo módulo, uma positiva na subida e uma negativa na descida.
Representação gráfica do movimento
Exemplos
1 - (UERJ) Um motorista, observa um menino arremessando uma bola
para o ar. Suponha que a altura alcançada por essa bola, a partir do
ponto em que é lançada, seja de 50 cm. A velocidade, em m/s, com que o
menino arremessa essa bola pode ser estimada em (use g = 10 m/s2):
a) 1,4
b) 3,2
c) 5,0
d) 9,8
e) 4,7
Resolução:
Na altura máxima V = 0 e ΔS = hmáx = 50 cm = 0,5 m
Equação de Torricelli: V2 = Vo2 + 2.a.ΔS → 02 = Vo2 - 2.10.0,5
Vo = √10 = 3,16 m/s
Alternativa b
2 - (Ufrs) Um projétil de brinquedo é arremessado verticalmente para
cima, da beira da sacada de um prédio, com uma velocidade inicial de 10
m/s. O projétil sobe livremente e, ao cair, atinge a calçada do prédio
com uma velocidade de módulo igual a 30 m/s. Indique quanto tempo o
projétil permaneceu no ar, supondo o módulo da aceleração da gravidade
igual a 10 m/s2 e desprezando os efeitos de atrito sobre o movimento do
projétil.
Resolução:
Atinge o solo com velocidade de – 30 m/s, pois está em movimento
retrogrado.
V = Vo – g.t
- 30 = 10 – 10.t
t = 4 s
♦ Queda livre
♦ Lançado verticalmente para baixo
Exemplos
1 - (CESGRANRIO) O Beach Park, localizado em Fortaleza-CE, é o maior
parque aquático da América Latina situado na beira do mar. Uma de suas
principais atrações é um toboágua chamado "Insano". Descendo esse
toboágua, uma pessoa atinge sua parte mais baixa com velocidade de 28
m/s. Considerando a aceleração da gravidade g = 9,8 m/s2 e desprezando
os atritos, conclui-se que a altura do toboágua, em metros, é de:
a) 40,0
b) 38,0
c) 36,8
Resolução:
V = 28 m/s / Vo = 0
Equação de Torricelli: V2 = Vo2 + 2.g.ΔS
282 = 02 + 2.9,8.ΔS
ΔS = 784/19,6
H = 40 m
Alternativa a
d) 32,4
e) 28,0
2 - (PUCCAMP) Dois tocos de vela caem da janela de um apartamento
bem alto. O intervalo de tempo entre a queda de um e do outro é de 1,0
s. Considere que eles estão em queda livre vertical, que a velocidade
inicial é nula e que a aceleração da gravidade é 10 m/s2. Quando o
segundo toco de vela completar 1,0 s de queda, a distância entre eles,
em metros, será igual a:
a) 25
b) 35
c) 15
d) 10
e) 5
Resolução:
Segundo toco (B) no instante 1s caiu: SB = gt2/2 = 5.1 = 5 m
Como o primeiro toco (A) partiu 1 s antes, quando t = 1 s para B, será
2 s para A: SA = 5tA2 = 5.22 = 20 m
ΔS = 20 – 5 = 15 m
Alternativa c
3 - (PUC-MG) Um helicóptero está descendo verticalmente e, quando
está a 100 m de altura, um pequeno objeto se solta dele e cai em direção
ao solo, levando 4 s para atingi-lo. Considerando-se g = 10 m/s2, a
velocidade de descida do helicóptero, no momento em que o objeto se
soltou, vale em km/h:
a) 25
b) 144
c) 108
d) 18
Resolução:
A velocidade inicial de descida (Vo) do objeto é a mesma que do
helicóptero - S = Vo.t + g.t2/2 → 100 = Vo.4 + 10.16/2 → Vo = 20/4
Vo = 5 m/s.3,6 = 18 km/h → Alternativa d
4 - (UNESP) Um corpo é lançado para baixo com velocidade de 15 m/s.
Sabendo que a altura inicial era de 130 m, determine o instante em que o
corpo se encontra a 80 m do solo. (g = 10 m/s2)
Resolução:
S = 130 – 80 = 50 m
S = V0t + gt2/2 →50 = 15t + 5t2
t2 + 3t – 10 = 0 → t = 2 s
5 - (UNESP) Um objeto é solto do repouso de uma altura de H no
instante t = 0. Um segundo objeto é arremessado para baixo com uma
velocidade vertical de 80 m/s depois de um intervalo de tempo de 4,0 s,
após o primeiro objeto. Sabendo que os dois atingem o solo ao mesmo
tempo, calcule H (considere a resistência do ar desprezível e g = 10
m/s2).
Resolução:
Objeto M, solto do repouso Vo = 0 → SM = H = gtM2/2 → H = 5tM2
Objeto N arremessado para baixo com velocidade inicial Vo = 80 m/s
S = Vo.tN + gtN2/2 → S = 80tN + 5tN2
Como M partiu 4s antes tM – tN = 4 → tM = tN + 4
H = 5.(tN + 4)2 → H = 5(tN2 + 8tN + 16) = 5tN2 + 40tN + 80
Se encontram no solo H = S → 5tN2 + 40tN + 80 = 80tN + 5tN2
40tN + 80 = 80tN → tN = 2 s
Substituindo tN = 2 s em S = H= 80tN + 5tN2 = 80.2 + 5.4=160 + 20
H = 180 m
Exercícios
1 - (UFPR) Cecília e Rita querem descobrir a altura de um mirante em
relação ao nível do mar. Para isso, lembram-se de suas aulas de física
básica e resolvem soltar uma moeda do alto do mirante e cronometrar o
tempo de queda até a água do mar. Cecília solta a moeda e Rita lá
embaixo cronometra 6 s. Considerando-se g = 10 m/s2, é correto afirmar
que a altura desse mirante será de aproximadamente:
a) 180 m
b) 150 m
c) 30 m
d) 80 m
e) 100 m
2 - (FUVEST) Numa filmagem, no exato instante em que um caminhão
passa por uma marca no chão, um dublê se larga de um viaduto para cair
dentro de sua caçamba. A velocidade v do caminhão é constante e o dublê
inicia sua queda a partir do repouso, repouso, de uma altura de 5 m da
caçamba, que tem 6 m de comprimento. A velocidade ideal do caminhão é
aquela em que o dublê cai bem no centro da caçamba, mas a velocidade
real v do caminhão poderá ser diferente e ele cairá mais à frente ou mais
atrás do centro da caçamba. Para que o dublê caia dentro da caçamba, v
pode diferir da velocidade ideal, em módulo, no máximo:
a) 1 m/s
b) 3 m/s
c) 5 m/s
d) 7 m/s
e) 9 m/s
3 - (UFPE) Uma pedra é lançada para cima, a partir do topo de um
edifício de 60 m com velocidade inicial de 20 m/s. Desprezando a
resistência do ar, calcule a velocidade da pedra ao atingir o solo, em m/s
(g = 10 m/s2).
4 - (CFT) Um elevador de bagagens sobe com velocidade constante de 5
m/s. Uma lâmpada se desprende do teto do elevador e cai livremente até
o piso do mesmo. A aceleração local da gravidade é de 10 m/s2. O tempo
de queda da lâmpada é de 0,5 s. Determine a altura aproximada do
elevador.
5 - (FUVEST) Um balão sobe verticalmente com movimento uniforme e, 5
s depois de abandonar o solo,seu piloto abandona uma pedra que atinge o
solo 7 s após a partida do balão. Pede-se: (g = 9,8 m/s2)
a) a velocidade ascencional do balão
b) a altura em que foi abandonada a pedra
c) a altura em que se encontra o balão quando a pedra chega ao solo
1 - Resolução:
g = 10 m/s2 / t = 6 s
Para a queda livre: h = gt2/2 = 10.62/2 → h = 180 m
Alternativa a
2 - Resolução:
Dublê: h = gt2/2 → 5 = 10t2/2 → t = 1 s
A velocidade ideal: Vi = ΔS/Δt = (L + 3)/1 → Vi = L + 3
Velocidade mínima: Vmin = ΔS/Δt = L/1 → Vmin = L
Velocidade máxima: Vmax = ΔS/Δt = (L + 6)/1 → Vmax = L + 6
V1 = Vi - Vmin = (L + 3) – L → V1 = 3 m/s
V2 = Vmax - Vi = (L + 6) – (L + 3) → V2 = 3 m/s
Alternativa b
3 - Colocando a origem no ponto de lançamento, a pedra sobe, atinge a
altura máxima e quando chega ao solo ocupa a posição S = - 60m
Instante em que ela chega ao solo: S = Vo.t – g.t2/2 → - 60 = 20t – 5t2
t2 - 4t – 12 = 0 → t = 6 s (instante em que ela chega ao solo)
Velocidade dela quando chega ao solo: V = Vo – gt → V = 20 – 10.6
V = - 40 m/s → em módulo: V = 40 m/s
4 - No instante em que a lâmpada se desprende do teto
do elevador ele está sendo lançada para cima com
velocidade de Vo = 5 m/s
Tempo de subida e descida até chegar ao piso: t = 0,5 s
S = Vot – gt2/2
- x = 5.0,5 – 5.(0,5)2
- x = - 1,25 m
altura do elevador = 1,25 m
5 - a) O balão sobe com velocidade constante V e, aos 5s atinge a altura
h, onde a pedra é abandonada com velocidade V: V = h/5
Velocidade inicial com que a pedra sobe: Vo = h/5
b) Observe que o movimento de sobe e desce da pedra demora 2 s e que
ela chega ao solo quando t = 2 s e na posição S = - h
S = Vo.t – gt2/2 → - h = h/5.2 – 4,9.22
h = 98/7 → h = 14 m
c) Cálculo da velocidade de subida do balão
que vale: V = Vo = h/5 = 14/5 → V = 2,8 m/s
O balão subiu durante 7 s com velocidade
constante de 2,8 m/s e percorreu:
V = ΔS/Δt
2,8 = H/7
H = 19,6 m