Tarefa extraclasse 2 Aline

Tarefa extraclasse 2
Aline Vieira Malanovicz - 10/04/08
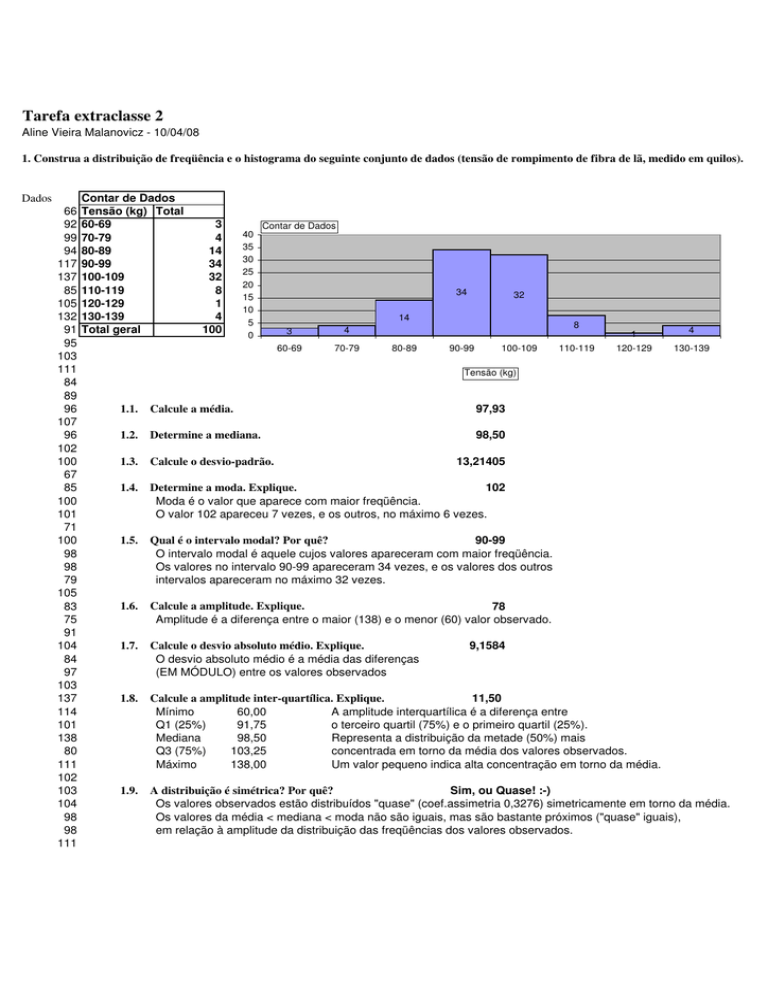
1. Construa a distribuição de freqüência e o histograma do seguinte conjunto de dados (tensão de rompimento de fibra de lã, medido em quilos).
Dados
66
92
99
94
117
137
85
105
132
91
95
103
111
84
89
96
107
96
102
100
67
85
100
101
71
100
98
98
79
105
83
75
91
104
84
97
103
137
114
101
138
80
111
102
103
104
98
98
111
Contar de Dados
Tensão (kg) Total
60-69
70-79
80-89
90-99
100-109
110-119
120-129
130-139
Total geral
3
4
14
34
32
8
1
4
100
40
35
30
25
20
15
10
5
0
Contar de Dados
34
32
14
3
4
60-69
70-79
80-89
8
90-99
100-109
110-119
1
4
120-129
130-139
Tensão (kg)
1.1.
Calcule a média.
97,93
1.2.
Determine a mediana.
98,50
1.3.
Calcule o desvio-padrão.
1.4.
Determine a moda. Explique.
102
Moda é o valor que aparece com maior freqüência.
O valor 102 apareceu 7 vezes, e os outros, no máximo 6 vezes.
1.5.
Qual é o intervalo modal? Por quê?
90-99
O intervalo modal é aquele cujos valores apareceram com maior freqüência.
Os valores no intervalo 90-99 apareceram 34 vezes, e os valores dos outros
intervalos apareceram no máximo 32 vezes.
1.6.
Calcule a amplitude. Explique.
78
Amplitude é a diferença entre o maior (138) e o menor (60) valor observado.
1.7.
Calcule o desvio absoluto médio. Explique.
O desvio absoluto médio é a média das diferenças
(EM MÓDULO) entre os valores observados
1.8.
Calcule a amplitude inter-quartílica. Explique.
11,50
Mínimo
60,00
A amplitude interquartílica é a diferença entre
Q1 (25%)
91,75
o terceiro quartil (75%) e o primeiro quartil (25%).
Mediana
98,50
Representa a distribuição da metade (50%) mais
Q3 (75%)
103,25
concentrada em torno da média dos valores observados.
Máximo
138,00
Um valor pequeno indica alta concentração em torno da média.
1.9.
A distribuição é simétrica? Por quê?
Sim, ou Quase! :-)
Os valores observados estão distribuídos "quase" (coef.assimetria 0,3276) simetricamente em torno da média.
Os valores da média < mediana < moda não são iguais, mas são bastante próximos ("quase" iguais),
em relação à amplitude da distribuição das freqüências dos valores observados.
13,21405
9,1584
104
99
94
86
106
102
100
87
84
91
98
96
92
95
99
93
86
111
92
101
104
104
102
102
77
94
87
110
94
97
99
95
99
102
60
96
102
109
92
88
101
88
100
122
104
91
96
115
107
103
98
2.
Se uma distribuição tem dois picos, o maior deles é a moda?
O que você faria se encontrasse uma distribuição com dois picos?
Cada pico pode ser a moda de uma das duas distribuições que devem existir nos
dados observados. Eu faria um teste t-student em alguma das variáveis dicotômicas,
para ver se de fato há duas distribuições juntas, que poderiam ser estudadas em separado. :-)
3.1.
3.2.
3.
Seguem-se quatro conjuntos de mensurações (em mm):
Calcule a média de cada conjunto.
106,2
105,9
105,8
106,7
105,9
107,1
106,4
105,9
106,5
106,2
106,5
104,6
106,5
106,3
105,2
106,6
107,4
106,3
106,9
106,4
Médias
106,10
106,42
105,82
106,72
106,27
Calcule a média de todas as 20 observações.
3.3. Calcule a média das quatro médias grupais.
Como esta se compara com a média já calculada anteriormente?
106,27
É igual. :-)
4.
A média (em geral) pode ser zero? Pode ser negativa? Explique.
Pode ser zero, se houver tanto valores positivos como valores negativos (ou todos iguais a zero).
Em geral, a média não é zero porque em geral medidas são valores positivos.
Também pode ser negativa, se houver valores negativos grandes em módulo.
Mas em geral, também não é negativa porque em geral também não ocorre essa outra condição.
5.
A mediana (em geral) pode ser zero? Pode ser negativa? Explique.
A mediana pode ser zero se metade dos valores observados for negativa, e a outra, positiva.
Como medidas são geralmente valores positivos, a mediana em geral não é zero.
A mediana pode ser negativa se metade dos valores observados for menor que um número negativo.
Como medidas são geralmente valores positivos, a mediana em geral não é negativa.
6.
Calcule o desvio-padrão de:
5
6
105
106
1050
1060
0,5
0,6
3
103
1030
0,3
2
102
1020
0,2
7
107
1070
0,7
Desvios-padrão
2,0736441
2,0736441
20,736441
0,2073644
6.1. Compare os resultados. Se o desvio-padrão de X é s, qual é o desviopadrão de X + c, onde c é uma constante? Qual é o desvio-padrão de cX?
O desvio-padrão de X+C é igual ao próprio s. Já o desvio-padrão de cX é igual a cs.
7.
O desvio-padrão (em geral) pode ser zero? Pode ser negativo? Explique.
O desvio-padrão pode ser zero, se todos os valores observados forem iguais.
Em geral, o desvio-padrão não é zero, porque há variabilidade entre os valores observados.
O desvio-padrão NÃO PODE ser negativo, por definição.
É definido como a raiz quadrada positiva da variância (que, por sua vez, é a soma de quadrados).
8.
O desvio absoluto médio (em geral) pode ser negativo? Explique.
O desvio absoluto médio NÃO PODE ser negativo, por definição.
É definido como a média das diferenças (EM MÓDULO) entre os valores observados.