ppt

V Escola Brasileira de
Supercondutividade
Recife, 10 a 14 de dezembro de 2001
Teorias Microscópicas para a
Supercondutividade
Raimundo Rocha dos Santos
[email protected]
Apoio:
Este mini-curso pode ser obtido do site
http://www.if.ufrj.br/~rrds/rrds.html
seguindo o link em “Seminários, Mini-cursos, etc.”
Esquema do mini-curso
I.
Supercondutividade convencional: vínculos
experimentais
II. Condução em Metais
III. Interação elétron-elétron
IV. Teoria BCS
V. Supercondutores de alta temperatura
VI. Conclusões
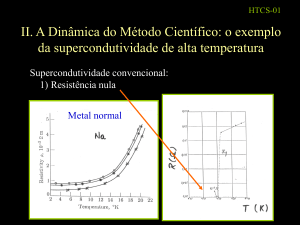
I. Supercondutividade convencional: vínculos
experimentais
1. Resistência nula
Metal normal
2. Efeito Meissner
Campo magnético não entra na
amostra: B = 0 no interior de
um supercondutor
[SUC não é condutor perfeito,
dentro do qual B/t = 0]
correntes superficiais aparecem de modo a gerar um
campo que se oponha ao
campo aplicado
Aplicações tecnológicas no dia-a-dia
 Levitação magnética
 Outras aplicações:
• geração de campos uniformes intensos (ressonância);
• deteção de campos fracos (SQUID); etc.
$
4He
N2
gelo
-269 -250 -200 -150
SUC’s convencionais
0
SUC’s de alta temperatura
T (°C)
3. Existência de um campo crítico
T [K]
Tipo II
Hc2 [kG]
Hc [G]
Tipo I
T [K]
para uma dada T, a amostra só é SUC
abaixo de um campo crítico
Existe também uma densidade crítica de corrente: Jc
log10 Tc
4. Efeito isotópico
 = 0.504
Hg
Tc  M

[M é a massa média dos isótopos
utilizados como íons da rede;
Reynolds et al., (1951)]
log10 M
ions participam ativamente
 fônons desempenham papel importante no
mecanismo da supercondutividade
CS/T
C/T [mJ/(mol K)]
C/T [mJ/(mol K)]
5. Calor Específico
CS/T  exp[-1.39Tc/T]
T 2 [K2]
Tc/T
Cs exponencial a baixas temperaturas
 gap no espectro
II. Condução em Metais
• Elétrons são férmions  Pauli: dois férmions não podem ter
conjuntos idênticos de números quânticos
• Gás de férmions [livres e independentes  (k,) definem
estados]: E  k2
Ex: Preenchendo os “níveis de energia de uma partícula” com 10
férmions
F
-4/L
-2/L
2/L
4/L
Considere cargas negativas em um potencial periódico
E
energia
energia

momento
k
i
momento
0 j0
k
i
i
0 j0
i
dens. de corrente
Elétron só é espalhado ( resistência) pq há estados
finais disponíveis
Como evitar dissipação: Suprimir,
através de algum mecanismo,
estados acessíveis na faixa de
energia próxima ao nível de Fermi
III. Interação elétron-elétron
elétron
íon
A interação Coulombiana entre um par qualquer
de elétrons é blindada pelos demais elétrons e
pelos íons
constante dielétrica 
4e 2
q2
4e 2 
(q)2 
 2  2
1  2

2
2
q 
q  k0    (q) 
4e 2
Interação elétron-elétron efetiva: Vkk’
k-q
k
q
k’+ q
k’
  k  k'
Dependência de Vkk’ com 
 retardamento devido ao fato
de que velast << vF
Frölich (1951) - Teoria de Perturbação:
4e 2 
g 2(q) 
Vkk'  2
1  2

2
2
q  k0    (q) 
cte. de acoplamento e-f
• (q)  D e k  F  102-103 hD
 interação via fônons só afeta elétrons com energias
muito próximas
• Se   D
 interação via fônons é maior em módulo: Vkk’ < 0
interação efetiva é atrativa
Então, se a interação entre elétrons pode, sob
certas circunstâncias, ser atrativa, deve-se
esperar que o espectro perto de F sofra mudanças
cruciais.
• O problema de Cooper
• O estado fundamental BCS
• Teoria BCS a temperatura finita
IV. A Teoria de Bardeen, Cooper e Schrieffer
1. O problema de Cooper (1956)
Dois elétrons interagindo atrativamente em presença de um
mar de Fermi preenchido podem formar um estado ligado?
(detalhes na 2a. e 3a. aulas)
Sim, com energia de ligação
dada por
F


E  2 D exp  1
vD( F )

intensidade da
interação e-e
Densidade de
estados no nível
de Fermi
 (|k|)  parte orbital simétrica  parte de spin anti-simétrica
 par num estado singlete: S = 0
2. O estado fundamental BCS (1957)
Elétrons, com energias próximas, interagindo atrativamente
aos pares:
Vkk'
k-q
k
q

v se  k   D e  k '   D


0 em outros casos
k’+ q
k’
Momento do CM do par se
conserva:
K = k + k’ = (k – q) + (k’+ q)
Aproximação: superfície de Fermi esférica
Para que dois elétrons interajam, eles devem ter energia
dentro de uma casca com a energia de Debye; que valor
de K otimiza os efeitos da interação?
K
kF
Para superfícies de Fermi esféricas, o maior número
de estados envolvidos ocorre quando K = 0
A Hamiltoniana BCS:
H 
k

(k ) ckck

 Vkk' bk bk '
k ,k '

bk  ck ck
termo livre (banda)
Solução variacional:
 
k
1  gk bk
1  gk2
0
Interlúdio: Densidade de estados quânticos
dN  D( E)dE
# de estados
no intervalo dE
D
densidade de estados
com energia E
d 1

D( E )  E 2
N.B.: gás de eletrons!
d=3
d=2
d=1
E
Densidades de estados (eletrons quase-livres ou tight-binding)
Isolante ou
Semicondutor
Metal
As somas em k podem ser expressas em integrais sobre energias:

k

Ld
2  
d

d d k 
 d D( )
(k )
A equação do gap (detalhes na 2a. e 3a. aulas):
1
k  
V0
V
kk'
k'
k'
, com Ek  (k )2  2k
2 Ek '
k  (k )(T )

1
onda - s


(k )  cos k x  cos k y onda - d x 2  y 2

sen k x sen k y onda - d xy


SUC’s
convencionais
A equação do gap fornece, então,
D

 D exp 1 vD( F )
2 senh1 vD( F )
onde supusemos acoplamento fraco: vD(F) << 1
Ek / F
 é o gap de energia para as excitações elementares, e Ek é
a energia das quase-partículas
k/kF
Noção elementar de quase-partículas (c.f. superfluidez em 4He):
A modificação no espectro pode ser esquematizada da seguinte
forma:
Estados
desocupados
F
2
Estados
ocupados
Gás de e `s
+ interação atrativa
Condução por pares (cada par tem KCM=k1+k2):
todos têm
KCM = 0

energia
energia
E
momento
momento
Para um par “sentir” a impureza teria que ser quebrado:
KCM  KCM dos demais pares
 alto custo energético (gap!)
Ao formarem pares, os elétrons “se vacinam” contra as
fontes de resistência
3. Teoria BCS a temperatura finita
H 

(k ) ck ck
k
1

V0

Vkk' bk bk '
k ,k '
Aproximação de Campo Médio:
bk bk '  bk bk'  bk bk '  bk bk '
Definição do gap:
1
 k (T )  
V0
 (k ) V
kk '
k'
bk '
=1 em BCS (s )
Interlúdio: Ordem de longo alcance não-diagonal, função de
onda macroscópica, e classe de Universalidade
• Em geral, são nulos os valores esperados de operadores
de criação e de destruição, mas não em SUC ou SUF
 ordem de longo alcance não-diagonal
• Analogia das super-correntes com movimento nãodissipativo de elétrons em átomos
 função de onda macroscópica: (r) = 0 ei(r)
 transf de Fourier: (k) = k/2Ek (parâmetro
de ordem)
• Função de onda complexa: 2 números
 classe de universalidade do modelo-XY
Solução auto-consistente + Transf de Bogoliubov (detalhes
nas aulas da tarde):
bk 
k
E
tanh k , com Ek  (k )2  2k
2 Ek
2
que fornece a equação do gap a T finita:
1
 k (T )  
V0
V
kk '
k'
k'
 Ek '
tanh
2 Ek '
2
( T)(0)
A equação do gap é
resolvida para (T ),
e, para   0, obtémse Tc
T/Tc
kBTc  0.567 D exp1 vD(F )

2(0)
 3.52
k BTc
usada para comparar com 
obtido em exp’s de tunelamento
Discrepâncias nesta razão e no efeito isotópico atribuídas
à simplicidade da interação elétron-fonon utilizada (p.ex.,
troca de um fônon apenas)
 deve-se ir além; p.ex., a teoria de acoplamento forte
de Eliashberg (os graus de liberdade fonônicos são
mantidos, ao invés de eliminados para construir
interação efetiva entre os elétrons)
A teoria BCS era “a teoria” microscópica da SUC até
1986, quando o primeiro supercondutor de alta Tc (30 K)
foi descoberto por Bednorz e Müller. Ainda OK para
carbetos de Boro (coexistência SUC+MAG) e para
MgB2 (acoplamento forte: Eliashberg)
V. Supercondutores de Alta Temperatura
O diagrama de fases:
Diferenças fundamentais entre os SUC’s:
 alta Tc (fonons: Tc < 30 K)
 estado normal metálico ou isolante (dep de x)
 proximidade de uma fase magnética
• tempo de vida das quase-partículas depende
fortemente da temperatura
• estado dos pares é predominantemente do tipo
onda-d
• pequenos comprimentos de coerência [  12 Å],
quando comparados com os convencionais [  500 Å]
• gap para excitações de spin abre-se acima de Tc
Taxa de relaxação spin-rede,
1/TT1, mede resp. mag. local
qa << 1;
Knight shift mede qa ~ 1.
Decréscimo de ambas quando
T  ligado à abertura de um
gap no espectro de excitações
de spin
• Resistividade linear com T
em intervalo apreciável
 não-líquido de Fermi??
T* Ť
Tc
Esta dependência,   T, com   2 e dependendo da dopagem
foi observada em outras amostras
eR=0
0
Tc
T

R=0
0
conv
Tc
HTCS
T*
T
Todas estas diferenças apontam para
um mecanismo não-fonônico: magnético
Estrutura cristalina:
Cálculos de bandas: caso não-dopado (x = 0):
Metal ????
Incluindo correlação, o
comportamento isolante
(correto!) é obtido
Ordenamento antiferromagnético: planos de CuO2
O
Cu

Descrição simplificada do isolante antiferromagnético dopado
transfere buraco do sitio j para i
H  t


ci c j
i , j ,
sítios de Cu
Favorece o salto do buraco
entre sítios
(Modelo de Hubbard)
 n
 H.c.  U
i  ni 
i
Repulsão Coulombiana: a
energia total aumenta se 2
e’s ocuparem o mesmo
orbital
 termo de correlação
S/ dopagem: energia é minimizada se colocarmos 1
buraco por sítio
os buracos tendem a ficar localizados nos sítios
 sistema é um isolante (Mott)
(para qq valor da repulsão Coulombiana)
C/ dopagem: buracos adicionais são “compartilhados”,
diminuindo o momento local  a tendência à ordem é
enfraquecida
O que o modelo simplificado prevê (2 dimensões)?
Teoria de Campo Médio
(teoria de 1 partícula)
Simulações de Monte Carlo
Este exemplo ilustra que a dimensão, d, do
sistema desempenha um papel crucial:
d   desvios do comportamento médio (flutuações) 
Teorias de Campo Médio podem
prever comportamentos pouco
realistas em d = 1 ou 2
Comportamento
magnético
razoavelmente bem explicado
pelo modelo simplificado:
dopagem tende a destruir
ordem AFM
E como explicar a fase AFM se
estender a uma dopagem não-nula?
multi-orbitais, 3a. dimensão, etc
Vejamos agora a fase “SG”:
Inicialmente pensou-se tratar de
uma fase de vidro de spin [spinglass], mas estudos experimentais e teóricos recentes
sugerem tratar-se de uma fase
listrada
Fase listrada melhor observada num “primo” dos supercondutores
Formação de
CDW [onda
de densidade
de carga]
novo ingrediente:
ordenamento
direcional dos
orbitais d do Mn
Acredita-se
que
nos
HTCS haja um equilíbrio
entre o ordenamento de
spin (AFM, nao SDW) e o
ordenamento de cargas
(tipo CDW) ao longo de
uma direção ( na Fig.):
As cargas tendem a se
agrupar em regiões de
menor ordem AFM
Ainda não se sabe como modificar o modelo de Hubbard –2D de
modo a produzir “stripes”, mas podemos tentar ver se ele pode
descrever um estado supercondutor
Simulações de MC para n =0.87, e
U = 4: suscetibilidade dependente de q
1
 (q ) 
Ns



d m iz  ( ) m iz (0) e iq
0
Pico em q = (,) não diverge, mas fica mais pronunciado à medida em que T 
 flutuações antiferromagnéticas de curto alcance
Várias teorias/modelos se baseiam na presença destas
flutuações AFM: os elétrons trocariam estas flutuações, de
modo análogo à troca de fônons nos SUC’s convencionais.
Partindo do modelo de Hubbard, uma T de Pert para estes
processos [Scalapino (1995)] fornece, para q = |k-k’|
grandes
3 2
Vkk'  U  (k  k' )
2
 pico em (, )
Eq do gap:
k  
1
V0

Vkk'
k'
k'
, com Ek  (k )2  2k
2 Ek '
Se V > 0,  tem que apresentar nós  onda d
Tomando a transf de Fourier, a interação efetiva no espaço real fica
interação on-site repulsiva
Veff
1
0
2
r
interação entre 1os. vizinhos atrativa
Modelo de Hubbard estendido
H  t
c

i c j
i , j ,
 n
 H.c.  U
i  ni 
i
V
( n
i
 ni  )(n j  n j )
i, j
(ver resultados em 1D nas transparências)
Isto nos remete ao modelo de Hubbard atrativo (on-site):
{a origem do U < 0 também pode ser atribuída a uma flutuação de
valência [Wilson (2001)] }
H  t
c

i c j
i , j ,
T
 n
 H.c.  U
i  ni 
i
T*
(região de pares pré-formados;
gap de spin)
Tc
|U|
VI. Conclusões
• Teoria BCS OK para SUC’s convencionais
• Recentemente: Tc de 40 K em MgB2 e de 55 K
em C60 dopados; só e-f é suficiente?
• SUC’s de alta Tc ainda sem teoria microscópica
bem estabelecida
• Mecanismo magnético ainda é o mais forte
candidato.
1986 + 46 = 2032. Será?