R - Instituto de Física / UFRJ

Sistemas Fortemente Correlacionados:
Supercondutividade e Magnetismo
Raimundo Rocha dos Santos
[email protected]
Apoio:
Esta apresentação pode ser obtida do site
http://www.if.ufrj.br/~rrds/rrds.html
seguindo o link em “Seminários, Mini-cursos, etc.”
Esquema do Mini-curso
I. Introdução
II. Supercondutores de alta temperatura
III. Problemas correntes
IV. Conclusões
Mecânica Quântica de um elétron: livre, numa caixa 3D
2 2
 2 k x2  k y  2 k z2
H


2m
2m
2m
H  E 
  Ae
ik x x ik y y ik z z
e
e
Condições de contorno periódicas (simula
invariância de translação em cristais):
2nx
, nx  0,1,2,...
L
quantização!
(analogame nte para y e z )
eikx ( x  L )  eikx x  k x 
L
 2 2
 E  (2nx  1)
L
 0
2

mL
elétron tem spin (atributo da matéria) ½ :  =  ou 
 estado de um elétron numa caixa:
|k,
Mecânica Quântica de um elétron: o átomo de H
2 2
e2
H 
 
   Rn (r )Ym ( ,  )
2m
40 r
s
p
Densidades de
probabilidade
d
n   e- mais longe do p+ e Eligação 
Mecânica Quântica de dois elétrons livres na caixa 3D:
distinguibilidade vs indistinguibilidade
 2 k12  2 k 22 2
H

; ki  kix2  kiy2  kiz2
2m
2m
H (r1 , r2 )  E (r1 , r2 )
Se as partículas são distinguíveis:
 (r1 , r2 )  a (r1 )b (r2 ); a (ri )  eik r 
a
Particulas indistinguíveis:
férmions
(S = 1/2, 3/2,…)
bósons
(S = 1,2,…)
i
a
Anti-simétrica se 1  2 =0 se a=b
1
a (r1 )b (r2 )  b (r1 )a (r2 )

2
Simétrica
se 1  2
1
a (r1 )b (r2 )  b (r1 )a (r2 )

2
Mecânica Quântica de N elétrons livres na caixa 3D
Para um gás de N elétrons tem-se a combinação simetrizada:

 Ca (r1 )b (r2 )c (r3 )... z (rN )
Por exemplo: sejam 5 elétrons ocupando 5 estados distintos (a,
b, c, d e e):
 a ( r1 )
 b ( r1 )
 ( r1 , r2 , r3 , r4 , r5 )   c ( r1 )
 d ( r1 )
 e ( r1 )
 a ( r2 )
 b ( r2 )
 c ( r2 )
 d ( r2 )
 e ( r2 )
 a ( r3 )
 b ( r3 )
 c ( r3 )
 d ( r3 )
 e ( r3 )
 a ( r4 )
 b ( r4 )
 c ( r4 )
 d ( r4 )
 e ( r4 )
 a ( r5 )
 b ( r5 )
 c ( r5 )
 d ( r5 )
 e ( r5 )
Princípio de exclusão de Pauli: se dois elétrons ocuparem o mesmo
estado (p.ex., c=d ), a função de onda se anula
Exemplo: alocando 10 elétrons nos níveis de energia
de uma partícula:
Nível de Fermi
F
-4/L
-2/L
2/L
4/L
Densidade de estados quânticos
dN  g( E )dE
# de estados
no intervalo dE
g
densidade de estados
com energia E
d 1

g( E )  E 2
N.B.: gás de eletrons
(i.e., sem rede)!
d=3
d=2
d=1
E
Importância de efeitos quânticos (indistinguibilidade):

Baixas densidades: não há interferência
Altas densidades: efeitos de interferência
Pressão do gás de elétrons a baixas densidades e/ou
altas temperaturas (contato com o gás ideal usual):

N
N

P  k BT 1  0.18
V
V



h


 2mk BT 


2
3
 2
2 
 N  
 o    
 V   

Pressão
Densidade
Desvio do gás ideal devido às correlações
introduzidas pela estatística de Fermi
O estado de cada elétron influencia os estados dos demais
Elétrons (independentes) em sólidos:
potencial cristalino periódico
a
a
elétrons quase-livres
[menos localizados]
a
limite atômico
[mais localizados]
dE
dE
Pergunta: quantos estados quânticos há
num intervalo de energia dE ?
Densidades de estados (elétrons quase-livres ou tight-binding)
Metal
Isolante ou
Semicondutor
Depende da magnitude do gap:
•isolante se  eV
•semicondutor se  0.1 eV
A aproximação de elétrons independentes com o modelo de bandas explica boa parte dos comportamentos
observados:
• metais
• isolantes
• semicondutores
Mas, cuidado com bandas estreitas (p.ex., d e f ):
maior tendência à localização

elétron passa mais tempo perto do núcleo

tem maior chance de encontrar outro elétron
no mesmo núcleo

interação repulsiva (Coulombiana) entre
elétrons não pode mais ser desprezada

os e se movimentam solidariamente, para
minimizar a energia fortemente correlacionados
Ilustração com a molécula de H2 :
1(r)
2(r)
+
+
 orb ( r1 , r2 )   ( r1 ) ( r2 )   1 ( r1 )   2 ( r1 ) 1 ( r2 )   2 ( r2 ) 
  1 ( r1 ) 1 ( r2 )   2 ( r1 ) 2 ( r2 )   1 ( r1 ) 2 ( r2 )   2 ( r1 ) 1 ( r2 )
2 elétrons em torno
de cada próton
1 e só 1 elétron em
torno de cada próton
Limite de forte repulsão entre os e: a presença de um e em torno de
um p+ inibe completamente a presença do outro e
 correlação extrema
Levando em conta o spin:
“Interação magnética” responsável pelo ordenamento magnético:
troca (exchange) = repulsão coulombiana + princípio de Pauli
Molécula de H2
Spins paralelos  elétrons mais
afastados  diminui atração dos
núcleos menor energia de
ligação
Energia (Ry)
Spins anti-paralelos  elétrons
mais próximos  aumenta
atração dos núcleos maior
energia de ligação
E  J S1  S2
Separação intermolecular (a0)
acoplamento de troca:
depende do recobrimento dos
orbitais atômicos
(Pausa para introduzir notação)
Partículas indistinguíveis
 não importa qual partícula está num dado estado, mas quantas
partículas estão naquele estado;
 se férmions, só 0 ou 1; se bósons, mais de 1;
 assim, podemos construir um espaço com esta info relevante,
na , nb , nc , nd , ne , n f , ng , nh ,...
onde os a, b, c, d,...podem ser, p.ex.,
• k
ou
• orbitais “atômicos” centrados nos sítios da rede
adicionand o partículas :
0,0,0,1,...  cd 0,0,0,0,...  cd 0
0,1,0,1,...  cb 0,0,0,1,...  cb cd 0
extraindo partículas :
1,1,0,1,...  cc 1,1,1,1,...
0,1,0,1,...  ca cc 1,1,1,1,...
operador número :
cb cb na nb nc nd ...  nb na nb nc nd ...
operador que transfere férmion de d para a :
ca cd na nb nc nd ...  (na  1) nd na  1 nb nc nd  1...
(Fim da pausa para introduzir notação)
Em resumo: um sistema é fortemente
correlacionado quando o movimento de uma
partícula influencia de modo fundamental o
movimento das demais, e vice-versa.
Conseqüência: a aproximação de
partículas independentes pode falhar
seriamente
P.ex., pode prever um comportamento
metálico para alguns isolantes
Por que sistemas fortemente correlacionados são importantes?
Ajuste coletivo entre carga e spin dá origem a
comportamentos interessantes:
• ordenamento magnético
• transição metal-isolante
• supercondutividade
• ondas de densidade de carga
• quantização da resistência (Efeito Hall Quântico Fracionário)
• efeito Kondo
• férmions pesados
•...
A explicação de vários destes comportamentos só foi
possível pela introdução de novos conceitos e idéias. E
muitos destes comportamentos ainda não foram explicados!
O entendimento destes sistemas se beneficia da introdução de
modelos simplificados:
•
•
•
•
explicita mecanismos mais importantes
“simplicidade”  cálculos factíveis
poder de previsão  comparação com dados experimentais
permite melhorias sistemáticas
Objetivos:
• determinar a natureza do estado fundamental
• determinar a natureza das excitações elementares
• entender sistemas inomogêneos
•...
Vamos ilustrar vários destes aspectos com um caso de estudo:
os supercondutores de alta temperatura (HTCS)
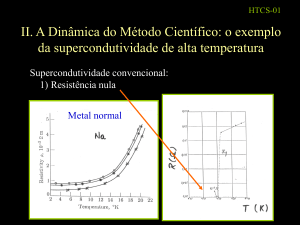
II. A Dinâmica do Método Científico: o exemplo
da supercondutividade de alta temperatura
Supercondutividade convencional:
1) Resistência nula
Metal normal
2) Efeito Meissner
Campo magnético não entra na amostra
 Levitação magnética
filme: http://www.fys.uio.no/super/
Aplicações tecnológicas no dia-a-dia?
$
4He
N2
gelo
-269 -250 -200 -150
SUC’s convencionais
0
SUC’s de alta temperatura
T (°C)
O diagrama de fases de um supercondutor de alta Tc
Diferenças fundamentais entre os SUC’s:
•alta Tc
•estado normal metálico ou isolante (dep de x)
•proximidade de uma fase magnética
Estrutura cristalina:
distância entre
planos de CuO2
~ 2  distância
Cu-O
 planos isolados
bom ponto de
partida
Cálculos de bandas: caso não-dopado (x = 0):
Metal ????
Incluindo correlação, o
comportamento isolante
(correto!) é obtido
Ordenamento antiferromagnético: planos de CuO2
O
Cu

Descrição simplificada do isolante antiferromagnético dopado
transfere buraco do sitio j para i
H  t
c

i
i, j

j i
c j  c c
sítios de Cu
Favorece o salto do buraco
entre sítios
(Modelo de Hubbard)
 U  n
n
i i
i
Repulsão Coulombiana: a
energia total aumenta se 2
e’s ocuparem o mesmo
orbital
 termo de correlação
S/ dopagem: energia é minimizada se colocarmos 1
buraco por sítio
os buracos tendem a ficar localizados nos sítios
sistema é um isolante (Mott)
(para qq valor da repulsão Coulombiana)
C/ dopagem: buracos adicionais são “compartilhados”,
diminuindo o momento local  a tendência à ordem é
enfraquecida
O que o modelo simplificado prevê (2 dimensões)?
Teoria de Campo Médio
(teoria de 1 partícula)
Simulações de Monte Carlo
Este exemplo ilustra que a dimensão, d, do
sistema desempenha um papel crucial:
d   desvios do comportamento médio (flutuações) 
Teorias de Campo Médio podem
prever comportamentos pouco
realistas em d = 1 ou 2
Comportamento
magnético
razoavelmente bem explicado
pelo modelo simplificado
E como explicar a fase AFM se
estender a uma dopagem não-nula?
multi-orbitais, 3a. dimensão, etc
Vejamos agora a fase SG:
Inicialmente pensou-se tratar de
uma fase de vidro de spin [spinglass], mas estudos experimentais e teóricos recentes
sugerem tratar-se de uma fase
listrada
Fase listrada melhor observada num “primo” dos supercondutores
Formação de
CDW [onda
de densidade
de carga] 
novo ingrediente:
ordenamento
direcional dos
orbitais d do Mn
Ondas de densidade de carga e ondas de densidade de spin
Separemos os elétrons em duas “espécies”: spin- e spin-
N.B.: Em 1-D não há ordem magnética de longo
alcance; a SDW é um estado quase-ordenado
Se período da CDW incomensurável com a rede
[i.e.,   r a; r racional e a
parâmetro de rede]
 transporte de corrente é
não-ômico
ômico
não-ômico
Explicação: analogia
mecânica
Acredita-se
que
nos
HTCS haja um equilíbrio
entre o ordenamento de
spin (AFM, nao SDW) e o
ordenamento de cargas
(tipo CDW) ao longo de
uma direção ( na Fig.):
As cargas tendem a se
agrupar em regiões de
menor ordem AFM
Vejamos agora a Supercondutividade:
Qual o mecanismo (i.e., o que torna alguns materiais) SUC?
Para responder a esta pergunta, voltemos aos SUC convencionais
log10 Tc
Efeito isotópico:
 = 0.504
Tc  M

(M é a massa do isótopo utilizado
como íon da rede)
log10 M
ions participam ativamente
 fônons
Frölich (1951): Um elétron pode atrair outro, via
interação com os fônons:
2 elétrons interagindo atrativamente em presença do mar de
Fermi formam um estado ligado: par de Cooper (1957)
Estados
desocupados
F

Estados
ocupados
Gás de e `s
+ interação atrativa
Conseqüência: abre-se um gap no espectro
energia
energia
Para entender o papel do gap, analisemos o processo de
condução em metais normais (cargas negativas):
momento
k
i
0 j0
k
i
momento
i
0 j0
i
dens. de corrente
Buraco só é espalhado ( resistência) pq há estados
finais disponíveis
KCM = 0
momento
energia
energia
Condução por pares:
momento
Para um par “sentir” a impureza teria que ser quebrado:
KCM  0  alto custo energético (gap!)
Ao formarem pares, os elétrons “se vacinam” contra as
fontes de resistência
Teoria BCS [Bardeen, Cooper & Scrieffer] (1957):
k BTc
 –h


1

D exp 


g
(

)
u
F


escala dede
energia:
determinada
intensidade
daestados
interacao
viadefonon
densidade
no e-e
nivel
Fermi
pelos fonons
 temperaturas limitadas a  30 K
HTCS: ausência de efeito isotópico sugestiva de outro mecanismo
eR=0
0
Tc
T

R=0
0
conv
Tc
HTCS
T*
T
Candidato: interação (magnética) entre spins
Até o momento não há teoria satisfatória para os HTCS!!!
III. Problemas correntes
• Física de Nanotubos
• Correlações eletrônicas em super-redes
• Coexistência entre supercondutividade e
magnetismo
• Semicondutores magnéticos diluídos
• (Supercondutores desordenados)
• Redes Ópticas
Nanotubos metálicos de carbono
Contatos de Au
Nanotubo de Carbono
(Pausa para falar de Nanociência e Nanotecnologia)
Propriedades físicas dos Nanotubos
de Carbono:
• suportam tensão longitudinal ~ 100 vezes
maior que aço (de mesmas dimensões),
com peso bem menor;
• resistência a dobras é das maiores
conhecidas;
• um CNT é a estrutura mais fina e dura,
feita pelo homem, capaz de se apoiar a si
própria e que é quimicamente inerte na
atmosfera.
• alguns tipos de CNT’s são bons
condutores;
• razão de aspecto comprimento/diâmetro é
uma das maiores conhecidas: ~cm/nm =
107
Ph. Avouris, IBM
Contatos de Au
Nanotubo de Carbono
STM = Scanning Tunnelling Microscope
Nanociência: ponto de encontro da Física, Biologia
e Química
(Fim da pausa para falar de Nanociência e Nanotecnologia)
Nanotubos de VOx, x ~ 0.24
+ doping
- doping
FM a T ambiente
Krusin-Elbaum et al., Nature 431, 672 (2004)
Modelo simplificado para estudar a competição entre correlações
eletrônicas e geometria (Monte Carlo Quântico; Bruno Camerano, IC)
Tubo Simples
Tubo Duplo
Supercondutividade e magnetismo em sistemas de camadas
Micro-camadas:
os carbetos de Boro
R = Sc, Y; Terras raras
RT2B2C
RTBC
T = Ni, Co, Pd, Pt
Coexistência entre ordens (antiferro) magnética (4f)
e supercondutora em alguns
compostos de uma
camada...
[Canfield et al., (1998)]
...mas não se consegue uma sistematização dos dados:
• RT2B2C  1 camada RC T=Ni
R=Sc, Y, Ce, Dy, Ho, Er, Tm, Lu, U, Th  SUC
coexistência SUC e MAG (exceto Lu)
R= Yb  Heavy fermion
• RTBC  2 camadas RC T=Ni  sem SUC, sem HF
• T=Co  1 camada
R=Lu, Tm, Er, Ho Dy, Gd, Ce  sem SUC
• R=La  1 camada
T=Ni  sem SUC; sem MAG
T=Pd, Pt  SUC
Necessário uma teoria simples – int e-fonon + BCS
OK! – que incorpore efeitos de camadas
Modelo*
U<0
U=0
U<0
U=0
U<0
U=0
            RT2B2C
            RTBC
U<0 U=0 U=0 U<0 U=0
U=0
T2B2
RC (sem elétrons f )
H  t  (ci ci 1  HC )  U i ni ni    i ni
i
*
T Paiva & RRdS [PRL (1986)]
i
i
sítios atrativos
35
L0=2
L0=1
30
I
25
20

=5/3
C= 0
DC= 0
I
15
S
10
M
5
0
0
5
10
|U|
15
20 0
M
S
5
10
15
20
|U|
Bom acordo com a experiência: a presença de uma
segunda camada de RC de fato desfavorece a SUC.
[T Paiva, M El-Massalami, & RRdS, em andamento (2002)]
Sistematização
10
SUC
Co Ni
Rh Pd
Ir Pt
5
Y
Nd Pr La
RPt2B2C
Y
Nd Pr La
RPd2B2C
La
RIr2B2C
Lu Yb TmEr Ho Y Dy Tb Gd Eu SmCe Nd Pr La
RNi2B2C
La
RRh2B2C
Lu Yb TmEr Ho Y Dy Tb Gd Eu SmCe Nd Pr La
RCo2B2C

Metal
0
0
| U4 |
8
12
16
Raio atômico
20
•Fixando os dados sobre a série do Ni, determina-se a fronteira SUC-M
•Adiciona-se as outras séries de metais de transição, respeitando o raio
atômico
•Pode-se prever, a partir daí, se determinado composto será, ou não, SUC
Próximas etapas:
• Incluir os momentos magnéticos (localizados) dos
elétrons f para investigar coexistência entre MAG
e SUC
• Estudar redes em 2D e 3D
Semicondutores magnéticos diluídos
Mn2+ substitui Ga3+ em GaAs
 cede um buraco [estado p]
p/ banda de valência,
enquanto que elétrons na
camada d contribuem com
spin S = 5/2
[Grande potencial de aplicações
tecnológicas (‘spintronics’)]
Os spins do Mn se ordenam ferromagneticamente abaixo
de Tc , cujo valor depende de x em Ga1-xMnxAs:
[F Matsukura et al., PRB (1998)]
Modelo simples:
Interação entre
um buraco e Mn é
AFM, tornando
FM a interação
efetiva entre os
Mn
= Mn, S =5/2
= buraco, S =1/2
Mas, como a densidade de buracos
depende da densidade de Mn?
Como varia a magnetização com a
densidade de Mn?
1buraco/
Mn
Há um aumento na
densidade de buracos ao
entrar na fase metálica
Quanto maior T, mais restrita
é a faixa de composições onde
os Mn se alinham
Questão a ser investigada:
natureza das transições
Metal-Isolante
Importante investigar
mecanismos que aumentem
a concentração de buracos
[RRdS, L E Oliveira, & J d’A. e Castro, (2002)]
Próximas etapas:
• Abandonar TCM: modelo microscópico em 1D para
testar o “gás de buracos” como mediador da interação
entre os Mn
• Simulação de aprisionamento de buracos devido a
defeitos na rede
IV. Conclusões
• Efeitos muito interessantes, característicos
de comportamentos coletivos
• Desafiadores por demandarem novas idéias
físicas
• Em geral, os (muitos) dados experimentais
disponíveis ainda aguardam explicações
teóricas.