(q) = a

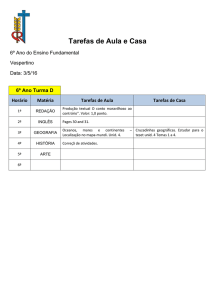
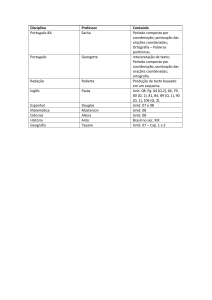
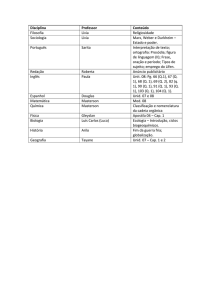
Unidade 4
O Monopólio
. Causas do monopólio
. Maximização do lucro em
monopólio
. O preço mark-up
. Efeito dos impostos sobre o
lucro do monopólio
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
1
Causas do monopólio
– Serviço público
– Patente de um produto
- Unica fonte de recurso natural
- Cartel constituido (OPEP)
– Grandes economias de escala :Não haver
capacidade “rentavel” para mais do que uma
empresa
- Ganho crescente de quota de mercado até
ficar com a totalidade do mercado
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
2
Monopólio Puro
Um único produtor (vendedor).
A curva de procura que um monopolio
enfrenta tem inclinação descendente
Deste modo, o monopolista pode
modificar o preço de mercado ajustando
o nível de produção.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
3
Monopólio Puro
$/unid.prod.
p(q)
Maior quantidade produzida
diminui o preço de mercado, p(q).
Nível de produção, q
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
4
Monopólio Puro
Suponha que o monopolio pretende
maximizar o lucro
 (q)  p(q)q  c(q)
Qual o nível de produção q* que
maximiza o lucro?
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
5
Monopólio Puro
Maximizando o lucro em ordem a q
d (q) d
 p(q)q   dc(q)  0

dq
dq
dq
Assim, para q = q*,
d
 p(q)q   dc(q) .
dq
dq
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
6
Curva de receita total
$
R(q) = p(q)q
q
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
7
Curvas de Receita e custo
$
R(q) = p(q)q
c(q)
q
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
8
Profit-Maximization
$
R(q) = p(q)q
c(q)
q
(q)
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
9
Profit-Maximization
$
R(q) = p(q)q
c(q)
q*
q
(q)
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
10
Profit-Maximization
$
R(q) = p(q)q
c(q)
q*
q
(q)
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
11
Profit-Maximization
$
R(q) = p(q)q
c(q)
q*
q
(q)
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
12
Profit-Maximization
$
R(q) = p(q)q
c(q)
q*
q
O nível de produção que maximiza o lucro
o declive das curvas de receita e de custo
total são iguais: Rm(q*) = Cm(q*).
(q)
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
13
Receita marginal
A receita marginal dá-nos o incremento de
receita pelo aumento de uma unidade de
produção q.
d
dp(q)
MR(q)   p(q)q   p(q)  q
.
dq
dq
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
14
Receita marginal
d
dp(q)
 p(q)q   p(q)  q
Rm (q) 
.
dq
dq
dp(q)/dq dá-nos o declive da inversa da
função de procura. Assim dp(q)/dq < 0.
Rm ( q )  p ( q )  q
dp ( q )
 p(q)
dq
Para q > 0.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
15
Receita marginal
Exemplo: Se p(q) = a - bq então
R(q) = p(q)q = aq - bq2
E assim,
Rm (q) = a - 2bq < a - bq = p(q) Para
q > 0.
a
p(q) = a - bq
a/2b
unid 4 Carlos Arriaga Costa
a/b q
Rm(q) = a - 2bq
U Minho - EEG Micro II 2º ano
Economia
16
Custo marginal
Custo marginal é o incremento do custo total
pelo aumento de uma unidade de produção.
dc ( q )
Cm( q ) 
.
dq
Exemplo Se c(q) = F + aq + bq2 então
Cm(q)  a  2bq.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
17
$
Custo marginal
c(q) = F + aq + bq2
F
q
$/Unid prod
Cm(q) = a + 2bq
a
q
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
18
Maximização do lucro
Exemplo
O Nível optimo q*,
Rm(q*) = Cm(q*). Assim se p(q) = a - bq e
c(q) = F + aq + bq2 então
Rm(q*)  a  2bq*  a  2bq*  Cm(q*)
E o nível d eprodução que maximiza o lucro é
q* 
unid 4 Carlos Arriaga Costa
a a
2(b  b )
U Minho - EEG Micro II 2º ano
Economia
19
E o preço de mercado será
p(q*)  a  bq*  a  b
unid 4 Carlos Arriaga Costa
a a
.
2(b  b )
U Minho - EEG Micro II 2º ano
Economia
20
$/unid produção
a
p(q) = a - bq
Cm(q) = a + 2bq
a
q
Rm(q) = a - 2bq
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
21
$/unid prod
a
p(q) = a - bq
Cm(q) = a + 2bq
a
q
q* 
a a
2(b  b )
unid 4 Carlos Arriaga Costa
Rm(q) = a - 2bq
U Minho - EEG Micro II 2º ano
Economia
22
$/unid prod
a
p(q) = a - bq
p(q*) 
a b
a a
2(b  b )
Cm(q) = a + 2bq
a
q
q* 
a a
2(b  b )
unid 4 Carlos Arriaga Costa
Rm(q) = a - 2bq
U Minho - EEG Micro II 2º ano
Economia
23
Preço de monopólio e elasticidade do preço
na função de procura
Suponha que o mercado se torna menos sensível às
mudanças de preço (ie a elasticidade preçoquantidade da procura fica menos negativa. Poderá o
monopólio explorar esta situação?
Rm ( q ) 
d
dq
 p(q)q  
p(q)  q
dp ( q )
dq

q
dp ( q ) 
 p ( q ) 1 
.
p(q)
dq


unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
24
Preço de monopólio e elasticidade do preço
na função de procura
Elasticidade preço quantidade da
procura é
p(q) dq

q dp (q)
unid 4 Carlos Arriaga Costa
assim
 1
Rm (q)  p(q) 1  .
 
U Minho - EEG Micro II 2º ano
Economia
25
Preço de monopólio e elasticidade do preço
na função de procura
Suponha que o custo marginal é constante.
Na maximização do lucro
 1
Rm (q*)  p(q*)1    k
 
No qual
p ( q*) 
k
1
1

1
1

p ( q*) 1    01 
0



Se e = -3 então p(q*) = 3k/2,
e se e = -2 então p(q*) = 2k.
Assim, logo que e aumenta até -1 o monopólio diminui o seu nível
De produção de modo a que o preço de monopólio aumente.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
26
.
Preço de monopólio e elasticidade do preço
na função de procura
1
 1    1.

Isto
é,
O monopolio maximiza a sua produção escolhendo
Um nível de produção onde a função de procura for elastica.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
27
Mark-up pricing
O preço de monopolio situa-se acima do
preço de competição perfeita .
Definimos a quantidade de Pm que excede
Ppc como o mark-up.
Quanto o monopólio poderá fazer de
“mark-up” e como é determinado?
Vamos estabelecer a associação entre o
mark-up e a elasticidade preço-quantidade
da função de procura, d.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
28
Preço Mark-up
A elasticidade preço-quantidade da função de
procura mede a percentagem de variação da
procura em resultado de uma quebra de 1% do
preço do bem
… d = -(P/q)(q/P)
Quanto maior for a sensibilidade dos
consumidores a uma alteração do preço, mais
elástica é a procura e maior d.
Quanto menor for a sensibilidade dos
consumidores a uma alteração do preço, menos
elástica é a procura e menor d.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
29
Preço Mark-up
Então em monopóio Rm=Cm. e
Cm = Rm = P+q(P/q)
Cm = P+q(P/q)(P/P)
Cm = P+P(q/P)(P/q)
P = Cm+P(1/d)
O mark-up do monopolio acima de Pc é:
P(1/d).
Mais (menos) elástica for a procura menor
(maior) é o mark-up.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
30
O índice de Lerner do poder de mercado
Rearranjando a expressão:
(P-Cm)/P = 1/d
É o Indice de Lerner do poder de
mercado
Mede a variação de preço relativamente
ao custo marginal
O indice de lerner será maior (menor),
mais (menos) elastica for a procura.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
31
Efeito dos Impostos sobre o
lucro do monopolio
Pode um monopolio transferir parte dos
seus impostos aos Consumidores?
Suponha o custo marginal constante por
cada unidade de produção.
Sem impostos, o preço do monopólio será
k
p(q*) 
.
1 
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
32
Efeito dos Impostos sobre o
lucro do monopolio
Uma quantidade de imposto $t/unidade
produção aumenta o custo marginal da
quantidade produzida por $t ou diminui o valor
do lucro por diminuição das receitas?.
Não importa, reduz em ambos o lucro
maximizado pela quantidade produzida,
provoca aumento de preço e a procura
diminui.
A quantidade de imposto causa distorções.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
33
Efeito dos Impostos sobre o
lucro do monopolio
Um imposto sobre os lucros a uma taxa A
uma taxa t reduz o lucro de (q*) para (1t)(q*).
Q: Como será o lucro após impostos (1t)(q*), maximizado?
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
34
Efeito dos Impostos sobre o
lucro do monopolio
Maximizando o lucro antes de impostos
(q*).
Então, neste caso, o imposto sobre os
lucros não influencia o nível de escolha da
quantidade produzida.
I.e. O imposto sobre os lucros tem um
efeito neutro
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
35
Efeito dos Impostos sobre o lucro do
monopolio
$/Unid produção
p(q)
p(q*)
Cm(q)
q
q*
Rm(q)
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
36
Efeito dos Impostos sobre o lucro do
monopolio
$/unid produção
p(q)
Cm(q) + t
p(q*)
t
Cm(q)
q
q*
Rm(q)
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
37
Efeito dos Impostos sobre o lucro do
monopolio
$/unid prod
Um aumento de imposto aumenta o preço e
uma diminuição da quantidade procurada
p(q)
p(qt)
p(q*)
Cm(q) + t
t
Cm(q)
q
qt q*
Rm(q)
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
38
Efeito dos Impostos sobre o lucro do
monopolio
p(q t )  p(q*) 
(k  t )
k
t


1 
1  1 
É a quatidade de imposto transferido aos
compradores. I.e se  = -2, a quantidade
de imposto transferido será de 2t.
Pois  < -1,  /1) > 1 e assim o monopolio
Transfere
aos consumidores mais do que o valor
Do imposto.
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
39
Efeito dos Impostos sobre o lucro do
monopolio
O imposto aumenta o custo marginal
em $(k+t)/unid produçao, alterando o preço
correspondente a maximização do lucro
(k  t )
p(q ) 
.
1 
t
O valor total de imposto pago pelos
compradores será de
p(q )  p(q*).
t
unid 4 Carlos Arriaga Costa
U Minho - EEG Micro II 2º ano
Economia
40