Gráfico de uma função afim

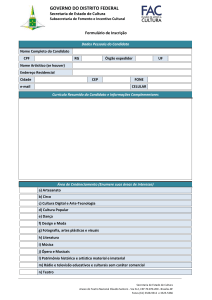
Função Afim
Profª: Mariane Krull
Colégio: CDC
Turma: 9º ano
Capítulo: 3
Função Afim
 Também chamada de função do 1º grau, ou seja, o maior expoente de x presente na
função vale 1.
 Sempre será definida pela lei de formação:
y= ax + b
Onde:
 a e b são números reais.
Função Afim
Gráfico de uma função afim
O gráfico de uma função
afim será sempre uma
reta.
Gráfico de uma função afim
(Exemplo 1) Esboce o gráfico de f(x) = x + 1
Resolução:
 y = x + 1  Função afim ( 1º grau);
 Sabemos que será uma reta;
 Para traçar uma reta, são necessários apenas dois pontos;
1º Passo) Montar a tabela com valores de x e y
Gráfico de uma função afim
(Continuação Exemplo 1) Construção do gráfico no caderno
Importante:
 O modo mais recomendado na construção de uma função é encontrar
os interceptos em x e em y.
 O que é intercepto? São os pontos onde a reta da função afim cortará
o eixo x e o eixo y.
y
Intercepto em y. ( 0; y).
x
Intercepto em x. (x ; 0).
Ângulo de declividade da função afim
 Quando a é positivo, o ângulo formado pela reta da função e o eixo x é
um ângulo agudo ( menos do que 90º).
Verifique essa condição na construção do gráfico da função
f(x) = x + 2
 Quando a é negativo, o ângulo formado pela reta da função e o eixo x é
um ângulo obtuso ( maior do que 90º).
Verifique essa condição na construção do gráfico da
função f(x) = -2x +1
Casos particulares da função afim
1º caso: Função linear
Toda função com lei de formação y = ax
Onde b=0
Exemplos:
a) y = 5x
b) y=-3x
c) y=-8x
O gráfico de uma função linear sempre passará
pela origem do plano cartesiano. Veja o exemplo
ao lado.
Casos particulares da função afim
2º caso: Função identidade
Toda função com lei de formação y = x
Onde b=0 e a=1
O gráfico de uma função identidade é a bissetriz
Dos quadrantes ímpares 1º e 3º. Veja abaixo o exemplo do gráfico de uma
função identidade.
2º Quadrante
3º Quadrante
1º Quadrante
4º Quadrante
Zero da função afim
É o valor de x, para o qual uma função f(x) se anula, ou seja, o valor de x, quando
y=0.
Exemplo: Qual o zero da função f(x) = 2x – 4
Resolução:
y = 2x – 4
0 = 2x – 4
2x = 4
x = 4/2
x=2
2 é o zero da função.
Geometricamente, é o ponto onde o gráfico corta o eixo x.
Zero da função
Coeficiente b
É o valor de uma função quando x = 0.
Exemplo: f(x) = 2x – 4
Resolução:
Quando x = 0
y=2x–4
y = 2. 0 – 4
y =. -4
Geometricamente, é o ponto onde o gráfico corta o eixo y.
EXERCÍCIOS
Função crescente e função decrescente
1º) Função crescente:
 Neste tipo de função, a medida que aumentamos os valores de x, os valores de
y também aumentam.
 Vamos verificar como isso ocorre graficamente através do exemplo abaixo:
Exemplo: Esboce o gráfico da função f(x) = 3x +1 e diga se ela é crescente ou
decrescente.
Resolução no caderno!
Importante: Em uma função crescente, o valor do coeficiente a será sempre
positivo.
Função crescente e função decrescente
2º) Função decrescente:
 Neste tipo de função, a medida que aumentamos os valores de x, os valores de
y decrescem.
 Vamos verificar como isso ocorre graficamente através do exemplo abaixo:
Exemplo: Esboce o gráfico da função f(x) = - x +1 e diga se ela é crescente ou
decrescente.
Resolução no caderno!
Importante: Em uma função crescente, o valor do coeficiente a será sempre
negativo.
Estudo do sinal de uma função afim
+++++++
2
-------- x
EXERCÍCIOS
FIM !
17