Lista - 1o ano - Matemática Villare

Matemática
Plantão dirigido9° ano ___Prof.: Larissa Vasconcelos
Nº:
Nome:
2º trimestre
SEMELHANÇA DE TRIÂNGULOS
Antes de iniciarmos o conteúdo, convém lembrar que os triângulos apresentam duas
propriedades exclusivas, que permitem reconhecer com maior facilidade quando dois
triângulos são semelhantes.
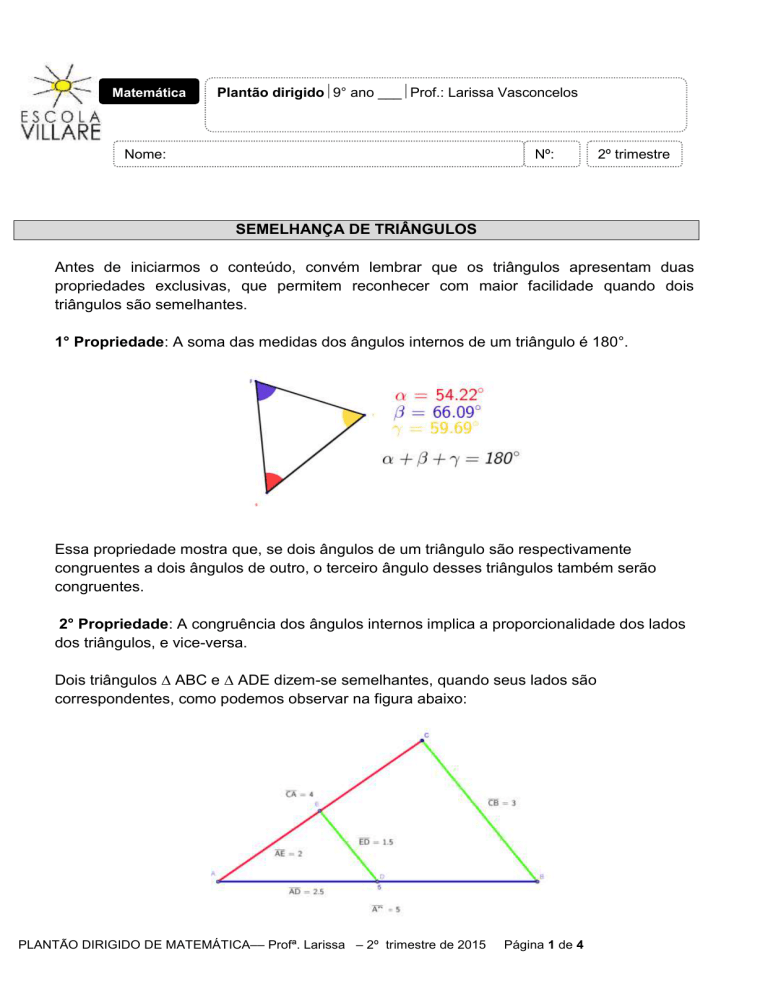
1° Propriedade: A soma das medidas dos ângulos internos de um triângulo é 180°.
Essa propriedade mostra que, se dois ângulos de um triângulo são respectivamente
congruentes a dois ângulos de outro, o terceiro ângulo desses triângulos também serão
congruentes.
2° Propriedade: A congruência dos ângulos internos implica a proporcionalidade dos lados
dos triângulos, e vice-versa.
Dois triângulos ∆ ABC e ∆ ADE dizem-se semelhantes, quando seus lados são
correspondentes, como podemos observar na figura abaixo:
PLANTÃO DIRIGIDO DE MATEMÁTICA–– Profª. Larissa – 2º trimestre de 2015
Página 1 de 4
Dessa forma, escrevemos ∆ABC ≅ ∆ ADE. Essa condição é atendida se:

Os ângulos correspondentes forem congruentes; e

Os lados forem proporcionais, ou seja:̅̅̅̅
= ̅̅̅̅
= ̅̅̅̅
𝐴𝐸
𝐴𝐷
𝐸𝐷
̅̅̅̅
𝐶𝐴
̅̅̅̅
𝐴𝐵
̅̅̅̅
𝐶𝐵
Essa razão entre lados correspondentes de triângulos semelhantes é chamada de razão de
semelhança.
Para semelhança de triângulos, também se deve analisar alguns critérios, são eles:
1° Critério LAL (lado/ângulo/lado): Se as medidas de dois dos lados de um triângulo são
respectivamente proporcionais às medidas de dois lados correspondentes de outro triângulo
e os ângulos determinados por estes lados são congruentes, então os triângulos são
semelhantes.
2° Critério AA (ângulo/ângulo): Se dois triângulos têm dois ângulos internos
correspondentes congruentes, então os triângulos são semelhantes.
PLANTÃO DIRIGIDO DE MATEMÁTICA–– Profª. Larissa – 2º trimestre de 2015
Página 2 de 4
3° Critério LLL (lado/lado/lado): Se as medidas dos lados de dois triângulos são
respectivamente proporcionais, então os triângulos são semelhantes.
̅̅̅̅
𝐴𝐶
̅̅̅̅
𝐴𝐵
̅̅̅̅
𝐶𝐵
4
5
3
Observe que :̅̅̅̅
= ̅̅̅̅
= ̅̅̅̅
→ 2 = 2,5 = 1,5 → 2 = 2 = 2. Com isso, tem-se que os lados do
𝐷𝐹
𝐷𝐸
𝐹𝐸
triângulos ABC são duas vezes a medida dos lados do triângulos DEF, respectivamente.
EXERCÍCIOS
1. Classifique as sentenças em verdadeiras ou falsas:
a) (
b) (
c) (
d) (
e) (
) Dois pentágonos regulares são sempre semelhantes.
) Dois triângulos equiláteros são sempre semelhantes.
) Dois pentágonos são sempre semelhantes.
) Dois quadrados são sempre semelhantes.
) Dois retângulos são sempre semelhantes.
2. Em cada item, temos pares de triângulos semelhantes. Identifique o caso de semelhança e
posteriormente os valores de "x" e "y".
a)
b)
A
E
A’
y
B
C B’
12
3
2
x
18
9
8
B
18
A
C
x
y
C’
4
D
3. Determine o valor de x nas figuras:
a)
b)
x
x
9
4
21
12
28
63
PLANTÃO DIRIGIDO DE MATEMÁTICA–– Profª. Larissa – 2º trimestre de 2015
Página 3 de 4
4. Na figura ao lado,
a)
b)
c)
d)
e)
AB // DE . Então x e y valem, respectivamente:
12 cm e 8 cm.
8 cm e 12 cm.
24 cm e 18 cm.
18 cm e 12cm.
10 cm e 14 cm.
15 cm
A
B
12 cm
18 cm
C
y
D
x
E
10 cm
5.No triângulo retângulo ABC abaixo, a medida de x, em cm, é:
a)
b)
c)
d)
e)
3.
6.
9.
12.
18.
C
C’
6 cm
A
B’
x
8 cm
B
12 cm
6. Na figura,
a)
b)
c)
d)
e)
BE // CD . Então o valor de x + y é igual a:
A
8
22
40
32
16
12 cm
16 cm
B
x
E
y
9 cm
C
D
35 cm
7. Para se calcular a largura L de um lago, usou-se o esquema representado pela figura abaixo, na qual
AB//CD. Nessas condições, a largura desse lago é:
a)
b)
c)
d)
e)
180
120
240
250
230
m.
m.
m.
m.
m.
B
D
L
A
PLANTÃO DIRIGIDO DE MATEMÁTICA–– Profª. Larissa – 2º trimestre de 2015
100 m
C
200 m
80 m
Página 4 de 4