Lab_2__Cto_RLC_resonante_fasores

Lab 1
Circuito RLC paralelo e Serie e freqüência de ressonância (uso de osciloscópio )
Leis de kirchoff das correntes CC e CA
Nome : .............................................................................................
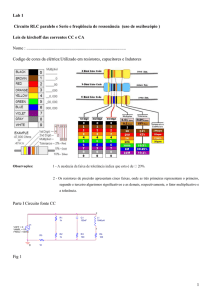
Codigo de cores da elétrica:Utilizado em resistores, capacitores e Indutores
Observações:
12 - Os resistores de precisão apresentam cinco faixas, onde as três primeiras representam o primeiro,
segundo e terceiro algarismos significativos e as demais, respectivamente, o fator multiplicativo e
a tolerância.
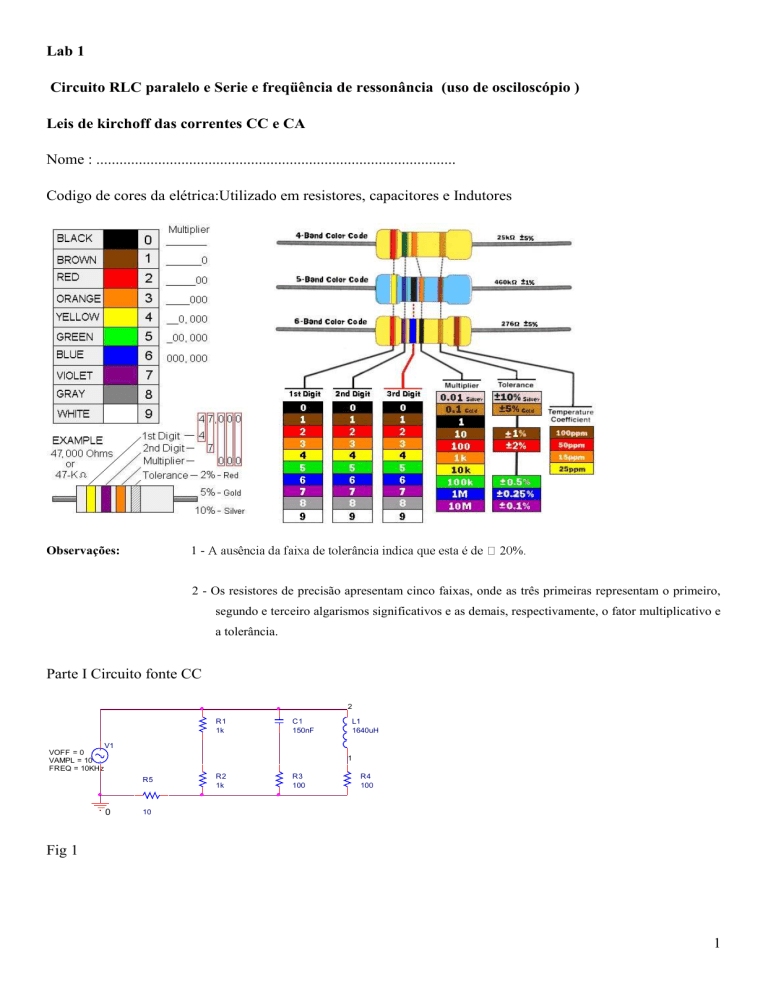
Parte I Circuito fonte CC
2
R1
1k
C1
150nF
R2
1k
R3
100
L1
1640uH
V1
VOFF = 0
VAMPL = 10
FREQ = 10KHz
1
R5
0
R4
100
10
Fig 1
1
1.- Com fonte de 10V continua meça corrente em R2 , R4 e R3(compare com valores teoricos) (0.5Ptos)
2.- Meça a corrente em R5 e verifique as leis de correntes de kirchoff (0.5ptos)
3.- Meça as tensões em R1+ R2+R5, verifiques e são cumpridas as leis de Kirchoff das tensões, explique(0.5
ptos)
4.-Meça as tensões em R4+L1+R5 , verifique as leis de kirchoff da tensões(0.5ptos)
Obs Em todos os casos realize as cálculos teóricos
Parte II Circuito Fonte CA ressonante paralelo
1.- Monte o circuito RLC paralelo (0.5ptos)
2.-Calcule a freqüência ressonante pela equação (0.5Ptos): 2f 
1
LC
3.-Determine experimentalmente as equações das correntes no resistor , capacitor e indutor em função do
tempo.(1pto)
4.- Meça os desfasamentos respeito a tensão de referência da corrente no capacitor e no indutor e as
amplitude da tensão em cada caso.(1pto)
5.- Expresse as correntes obtidas experimentalmente no resistor, capacitor e indutor em forma fasorial da
fig 2(0.5pto)
6.- Calcule as correntes no resistor, capacitor e indutor e expresse os resultados em forma fasorial e compare
com os valores experimentais (1pto)
7.- Meça a corrente total através do resistor shunt(R11) e verifique leis de kirchoff (em modulo e fase) das
soma das correntes (1pto)
8.- Obtenha experimentalmente as formas fasoriais das tensões no capacitor, indutor e resistor(0.5ptos)
9.- Calcule as tensões no resistor, capacitor e indutor da fig 1 e expresse os resultados em forma fasorial e
compare com os valores experiementais (1ptos)
10.- Faça um diagrama vetorial das somas das correntes(0.5 ptos)
11.-Os erros encontrados a que pensa você que se deve? (0.5ptos)
2
Lembrando de Física III
Reatância Capacitiva Xc(s)
I C (t )  C
dVc (t )
dt
/  Aplicando Laplace
I C ( s )  CV( s )
V
1
 C ( s )  X C ( S ) =Reatância capacitiva
C I c ( s )
Reatância Indutiva XL(s)
VL (t )  L
diL (t )
dt
/
VL ( s )  LI L ( s )
VL ( s )
I L(s)
 L  X L ( s ) =Reatância Indutiva
3