fatoração: fator comum em evidência

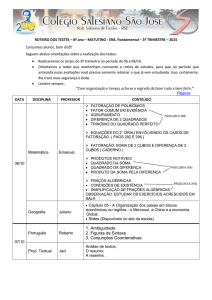
Matemática
Plantão dirigido8° ano ___Prof.: Larissa
Nº:
Nome:
3º trimestre
FATORAÇÃO
FATORAÇÃO: FATOR COMUM EM EVIDÊNCIA
Nesse modelo de fatoração temos que determinar o elemento comum aos termos que
formam o polinômio. Observe:
No polinômio x2 + 2x, temos que a variável x é comum aos dois termos. Ela será o
termo em evidência, a qual dividirá os termos do polinômio original.
x2 + 2x = x (x+2)
Exemplos de fatoração utilizando fator comum em evidência:
Exemplo 1:
Exemplo 2:
4x3+2x2 = 2x2 (2x + 1)
16x – 8x2 = 8x (2 – x)
FATORAÇÃO: AGRUPAMENTO
Na fatoração por agrupamento, utilizamos inicialmente quando necessário a
associação dos monômios, em seguida aplicamos a fatoração por evidência e logo por
fim agrupamos os termos sob certas condições também de evidenciação. Observe:
2yx – x – 6y + 3
Vamos aplicar evidência entre 2yx e – x e entre – 6y e 3.
- Fator comum entre 2yx e – x = x
- Fator comum entre – 6y e 3 = 3
Plantão dirigido de matemática –– Prof.: Roberdan – 3º trimestre de 2015
Página 1 de 5
Portanto:
- x (2y + 1) + 3 (2y + 1)
Podemos continuar colocando mais um termo em evidência, qual termo é comum entre
–x (2y + 1) e 3 (2y + 1) ?
- O fator comum entre esses dois termos é o (2y + 1), portanto temos:
(2y + 1).(-x + 3)
Observe mais alguns exemplos de fatoração por agrupamento:
Exemplo 1:
bx – 2b + x – 2 = b(x – 2) + 1(x – 2) = (x – 2).(b + 1)
Exemplo 2:
10x² + 15xy + 4x2 + 6y = 5x (2x + 3y) + 2x (2x + 3y) = (5x + 2x) (2x + 3y)
PRODUTOS NOTÁVEIS
1º caso – Quadrado da soma:
Podemos expressar o quadrado da soma pela generalização (x + y)2 ou (x + y)(x + y).
O cálculo (x + y)(x + y) pode ser resolvido aplicando a propriedade distributiva da
multiplicação. Temos:
x.x + x.y + x.y + y.y = x2 + 2xy + y2
Regra prática:
- “O quadrado do primeiro termo, mais duas vezes o primeiro termo pelo segundo,
mais o quadrado do segundo termo.”
Plantão dirigido de matemática –– Prof.: Roberdan – 3º trimestre de 2015
Página 2 de 5
2º caso – Quadrado da diferença
Generalizando temos (x – y)2 ou (x – y)(x – y):
x.x – x.y – x.y + y.y = x2 – 2xy + y2
Regra prática:
- “O quadrado do primeiro termo, menos duas vezes o primeiro termo pelo
segundo, mais o quadrado do segundo termo.”
EXERCÍCIOS
1) Fatore as expressões
a) 12x3+18x2+6
b) ax+ay+2x+2y
c) a2x3-bx2+a2x-b
d) 12x+6y
e) 3a2x3 - 6ax2 + ax – 2a
f) ax3+ayz+az2
g) ax+ay
h) 3am+bm+3an+bn
i) 2x+2y
j) 12x4-14x3+70x2+18x-8
Plantão dirigido de matemática –– Prof.: Roberdan – 3º trimestre de 2015
Página 3 de 5
k) 5h2 - 3h
l) am + na - ap
m) 4x3 - 6x2 + 2x - 3
n) a2x3 - b2x
o) x2y – y - 2x2 + 2
p) 5x3 + 10x2 + 20x
q) mp + Np
r) ac – bc + ad – bd
2) Encontre o conjunto solução das equações abaixo:
a) 7x² + 14x = 0
b) x² - 5x = 0
b) 4x² -12x = 0
Plantão dirigido de matemática –– Prof.: Roberdan – 3º trimestre de 2015
Página 4 de 5
c) x² - 7x = 0
c) 21x² - 42x = 0
d) x2 + 4x = 0
e) 2x2 + 4x = 0
3) Utilizando as regras dos produtos notáveis, calcule:
a) (x - 3)2
b) (x+2)2
c) (4x+3y)2
d) (x - 1)2
f) (3y - 2x)2
g) (6a - b)2
3 2
h) (2𝑚 + 4)
i) (7x+1)2
Plantão dirigido de matemática –– Prof.: Roberdan – 3º trimestre de 2015
Página 5 de 5