Universidade Federal da Bahia

Universidade Federal da Bahia - DEE
Dispositivos Eletrônicos – ENG C41
Professora: Ana Isabela Araújo Cunha
Segunda Avaliação – Semestre 2010.1
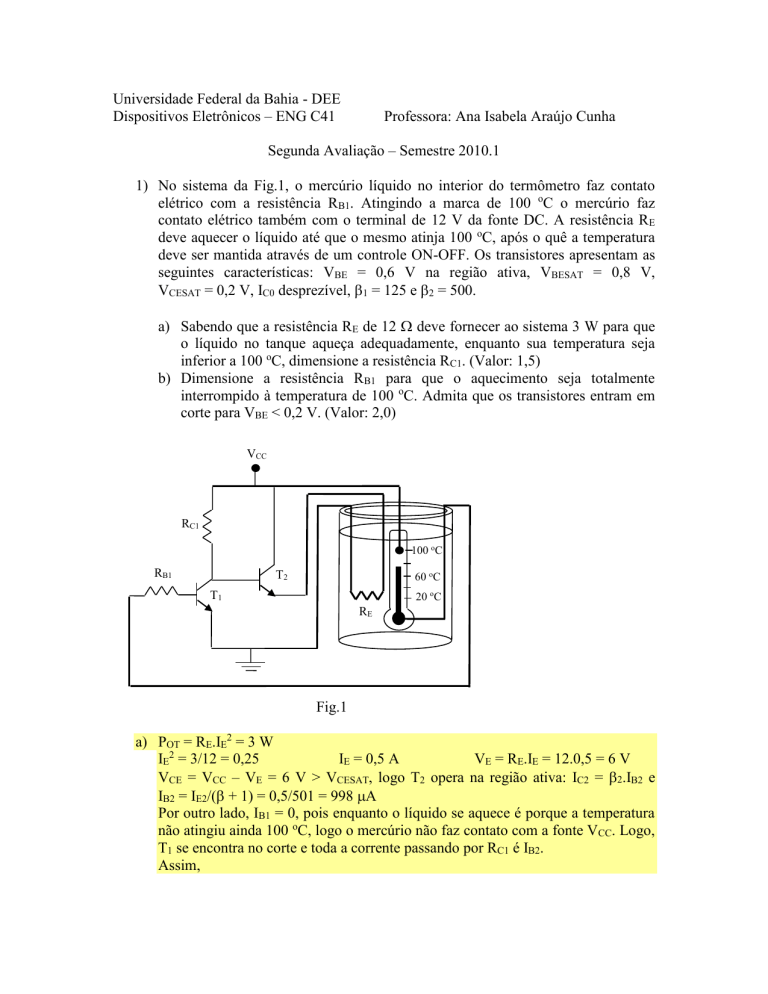
1) No sistema da Fig.1, o mercúrio líquido no interior do termômetro faz contato
elétrico com a resistência RB1. Atingindo a marca de 100 oC o mercúrio faz
contato elétrico também com o terminal de 12 V da fonte DC. A resistência RE
deve aquecer o líquido até que o mesmo atinja 100 oC, após o quê a temperatura
deve ser mantida através de um controle ON-OFF. Os transistores apresentam as
seguintes características: VBE = 0,6 V na região ativa, VBESAT = 0,8 V,
VCESAT = 0,2 V, IC0 desprezível, 1 = 125 e 2 = 500.
a) Sabendo que a resistência RE de 12  deve fornecer ao sistema 3 W para que
o líquido no tanque aqueça adequadamente, enquanto sua temperatura seja
inferior a 100 oC, dimensione a resistência RC1. (Valor: 1,5)
b) Dimensione a resistência RB1 para que o aquecimento seja totalmente
interrompido à temperatura de 100 oC. Admita que os transistores entram em
corte para VBE < 0,2 V. (Valor: 2,0)
VCC
RC1
100 oC
RB1
T2
60 oC
T1
20 oC
RE
Fig.1
a) POT = RE.IE2 = 3 W
IE2 = 3/12 = 0,25
IE = 0,5 A
VE = RE.IE = 12.0,5 = 6 V
VCE = VCC – VE = 6 V > VCESAT, logo T2 opera na região ativa: IC2 = IB2 e
IB2 = IE2/( + 1) = 0,5/501 = 998 A
Por outro lado, IB1 = 0, pois enquanto o líquido se aquece é porque a temperatura
não atingiu ainda 100 oC, logo o mercúrio não faz contato com a fonte VCC. Logo,
T1 se encontra no corte e toda a corrente passando por RC1 é IB2.
Assim,
VCC  R C1 I C1  VBE  R E I E
R C1 
12  0,6  6  5.410 ,8 
998 x10 6
b) A 100 oC, o contato se estabelece entre RB1 e VCC, fazendo T1 conduzir. Para que
o aquecimento se interrompa, não deve haver corrente em RE, portanto T2 deve
estar em corte. Assim, façamos T1 entrar em saturação, pois neste caso teríamos:
VBE2 = VCE1 < VCESAT = 0,2 V.
Então:
I B1 
 V  VCESAT  12  0,2  17,447 A
VCC  VBESAT
I V
 I B1 lim  C1 CESAT  CC
R B1
1
1 R C1
125 x 5410 ,8
R B1 
12  0,8
17 ,447 x10 6
 641,959 k
2) No circuito de polarização automática da Fig.2, RC = 3009 , RE = 4941,58 ,
RB1 = RB2 = 75 k, RB3 = 25 k, VCC = 12 V e o TBJ tem como características:
 = 100, VBE = 0,634 V na região ativa e IC0 desprezível.
a) Determine os novos valores das resistências RC e RE para que o ponto de
polarização permaneça o mesmo ao se fechar a chave. (Valor: 2,5)
b) Determine a variação percentual em IC em cada caso (chave aberta ou
fechada) para uma variação de 20 % em , e o mesmo ponto de polarização.
(Valor: 1,0)
VCC
RB1
IC
RC
+
VCE
-
RB3
RB2
RE
Fig.2
a) Antes do fechamento da chave, o equivalente de Thévenin visto da base, à
esquerda, é:
VBB 
R B2
VCC  0,5VCC  6 V
R B1  R B2
RB 
R B1 R B2
75000

 37 ,5 k
R B1  R B2
2
Assim,
IB 
VBB  VBE
6  0,634

 10 A
R B    1R E 37500  101 x 4941 ,58
I C  I B  1 mA
I E  I C  I B  1,01 mA
VCE  VCC  R C I C  R E I E  4 V
Com a chave fechada, o equivalente de Thévenin visto da base passa a ser:
VBBX 
R B2 // R B3
VCC  0,2VCC  2,4 V
R B1  R B2 // R B3
R BX  R B1 // R B2 // R B3 
37500 x 25000
 15 k
37500  25000
Assim,
VBBX  R BX    1R EX I B  VBE
R EX 
VBBX  VBE  R BX I B 2,4  0,634  15000 x10 x10 6

 1600 
IE
1,01x10 3
R CX I C  VCC  VCE  R EX I E  12  4  1600 x1,01x10 3  6,384 V
R CX  6384 
b) A variação percentual de IC em termos da variação percentual de IB é:
I C
1
x100 
IC

R E
1 
R
E  RB


x100
 


Para o caso da chave aberta:
I C
1
x100 
IC

100 x 4941 ,58
1 
4941 ,58  37500




20  1,582 %
Para o caso da chave fechada:
I C
1
x100 
20  1,88 %
IC
100 x1600 

1 

 1600  15000 
3) No circuito da Fig.3, M1 e M2 fazem um divisor de tensão para fixar um potencial
constante no terminal de porta da fonte de corrente M3. Sabendo que W1/L1 =
64,8, W3/L3 = 5, VDD = 5 V, VT0N = 0,75 V, VT0P = -1,0 V, nN = nP = 1,25,
NC'ox = 100 A/V2, PC'ox = 75 A/V2 e que todos os transistores são muito
longos:
VDD
M1
M3
vOUT
IOUT
RL
M2
Fig.3
a) Dimensione a razão de aspecto de M2, W2/L2,para que a corrente de saída seja
IOUT = 150 A. (Valor: 2,0)
b) Determine o máximo valor da resistência de carga RL para que a fonte opere
adequadamente. (Valor: 1,0)
a)
Para facilitar a resolução, vamos identificar todos os terminais no diagrama do circuito:
S1 ≡ B1 ≡ S3 ≡ B3
VDD
M3
M1
D3
vOUT
G1 ≡ G 2 ≡ D 1 ≡ D2 ≡ G 3
IOUT
RL
M2
S2 ≡ B2
I OUT  I D3   P Cox

V
n P W3
VP3  VSB3 2 1  DS3
2 L3
VA3


   P Cox n P W3 VP23

2 L3

(sendo VSB3 = 0 e o efeito Early desprezível, ou seja, VA3 infinita)
VP23 
I OUT
150

 0,64
1,25
n P W3
75 x
x5
 P Cox
2
2 L3
VP 3  0,8 V
I D 2  I D1   P C ox

V
n P W1
VP1  VSB1 2 1  DS1
2 L1
VA1


   P C ox n P W1 VP 3 2

2 L1

1,25
x 64 ,8x 0,64  1,944 mA
2
(VSB1 = 0 e o efeito Early é desprezível em M1 também. Além disto, VP1 = VP3)
I D 2  75 x10 6 x

   N Cox n N W2 VP 2 2  1,944 mA

2 L2

(mais uma vez, VSB2 = 0 e o efeito Early é desprezível em M 2)
I D 2   N Cox

V
n N W2
VP2  VSB 2 2 1  DS2
2 L2
VA 2

VDD = -VGB1 + VGB2
VP1 
VGB1  VT 0 P
nP
VGB1  n P VP1  VT 0 P  1,25 x (0,8)  1  2 V
VGB2  VDD  VGB1  5  2  3 V
VP 2 
W2

L2
VGB2  VT 0 N 3  0,75

 1,8 V
nN
1,25
I D2
1944

 9,6
n
1,25
2
1,82
100
 N Cox N VP 2 
2
2
b) Para M3 operar em saturação, devemos ter: vDB3 < VP3
vDB3 = vOUT – VDD
vOUT – VDD < VP3
vOUTmáx = VDD + VP3 = 5 – 0,8 = 4,2 V
RLmáx = vOUTmáx/IOUT = 4,2/150x10-6 = 28 k
************************************************************************
Formulário
TBJ na região ativa: IC = IB + ( + 1)IC0
I
I
IC
S   C  C 
na polarização automática



R E 

1 
 RE  RB 
MOSFET em inversão forte ( VSB  VP ), com VP 

 na região de saturação ( VDB  VP )


VT0, VDB, VSB e VGB > 0 no MOSFET canal N e VT0, VDB, VSB e VGB < 0 no MOSFET
canal P
I D  Cox

V
Wn
VP  VSB 2 1  DS
L 2
VA

VGB  VT 0
:
n