Fase entre corrente e tensão em

Fase entre corrente e tensão em
Circuitos RC e RLC em série
Introdução:
Neste experimento analisaremos a diferença de fase entre corrente e tensão no circuito
RLC em série. Também estudaremos as figuras de Lissajous gerado por esta diferença de
fase.
Modelo Teórico:
Sabemos que as reatâncias indutivas e capacitivas são dados por, respectivamente:
X L  W .L
1  onde:
XC 
W .C
W= freqüência angular
L=Indutância
C= Capacitância
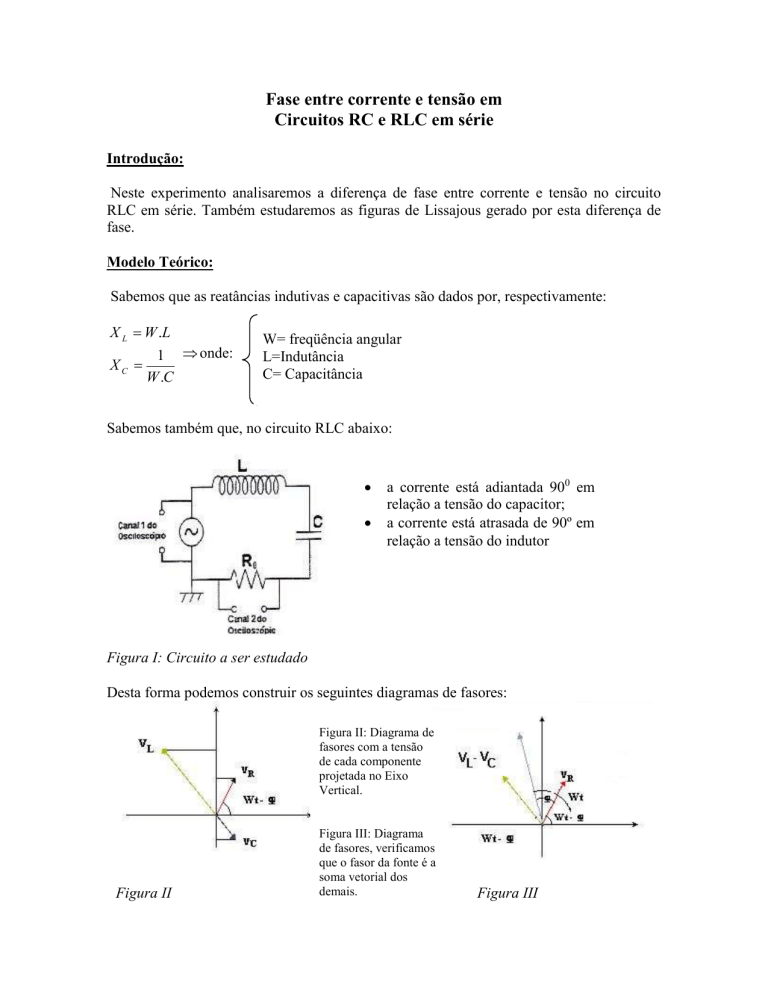
Sabemos também que, no circuito RLC abaixo:


a corrente está adiantada 900 em
relação a tensão do capacitor;
a corrente está atrasada de 90º em
relação a tensão do indutor
Figura I: Circuito a ser estudado
Desta forma podemos construir os seguintes diagramas de fasores:
Figura II: Diagrama de
fasores com a tensão
de cada componente
projetada no Eixo
Vertical.
Figura II
Figura III: Diagrama
de fasores, verificamos
que o fasor da fonte é a
soma vetorial dos
demais.
Figura III
Da figura III, obtemos:
tg 
VL  VC IX L  IX C
X  XC

 tg  L
VR
IR
R
Sabemos da mecânica elementar que:
S  v  t  S 0  0  S  v.t
Dividindo ambos os lados por r:
s v
s
  t 
,representa o deslocamento angular.
r r
r
v
,representa a velocidade angular.
r
  w.t
2

t
t
Sabemos que a corrente no circuito RLC segue a seguinte equação:
I (t )  I MAX  senwt   
Se substituirmos, I(0) = i0, obtemos:
i0  I MAX  sen 0   
sen    
i0
I MAX
Como   é um número positivo, temos
 i
   arcsen  0
 I MAX



Podemos obter facilmente estes dados utilizando o modo x.y do osciloscópio. Num canal
colocamos um sinal proporcional a corrente (a tensão do resistor R) para localizarmos IMAX.
No outro canal colocamos o sinal do gerador, para podermos localizar i0.
Previsão
Para os valores teóricos de R, L e C, esperamos obter o seguinte gráfico de   w :
Gráfico teórico de  em função de 
2
1,5
1
0,5
0
-0,5 0
5000
10000
15000
20000
25000
30000
-1
-1,5
-2
Figura IV: previsão do gráfico
Sabemos que o indutor utilizado apresenta uma resistência interna, então usaremos a
X  XC
seguinte correção tg  L
R  RL
Prevemos também que, as figuras mostradas pelo osciloscópio no modo xy serão figuras de
Lissajous, conforme as figuras abaixo:
Figura V: Figura com
Lissajous com 
próximo de 90º
Figura VI: Figura com
Lissajous com  = 90º
Figura VII: Figura com
Lissajous com  = 0º
Para o caso da Figura VII, podemos calcular a freqüência f0
X  XC
1
1
tan 0 0  L
 X L  X C  W0 L 
 W02 
R
W0 C
LC
W0  2f  f 0 
1
2
1
LC
No Experimento esperamos encontrar f 0  1516 Hz
w0  9534,6rad
Dados Experimentais
Tabela 01
Frequencia Periodo(ms)
157
6,385
202
4,94
343
2,916
620
1,625
886
1,1285
1090
0,916
1260
0,7935
1491
0,6708
1638
0,6104
1797
0,5564
2000
0,499
2420
0,4136
2960
0,3378
3958
0,2527
5400
0,1859
6855
0,1459
7865
0,12715
t(ms)
-1,6
-1,2
-0,69
-0,38
-0,23
-0,09
-0,011
0,000
0,05
0,08
0,09
0,09
0,07
0,06
0,04
0,04
0,03
Erro (ms)
0,2
0,2
0,05
0,05
0,05
0,05
0,005
0,01
0,01
0,01
0,01
0,005
0,005
0,005
0,002
0,002
rad)
-1,55894
-1,55729
-1,47955
-1,45696
-1,28828
-0,6376
-0,0831
0
0,526763
0,889403
1,09491
1,305803
1,306939
1,414056
1,449231
1,51512
1,494062 Tabela 01
Gráfico da defasagem da corrente em relação a
tensão por freqüência
Defasagem (rad)
2
1,5
1
0,5
0
-0,5 0
-1
Seqüência1
2000
4000
6000
8000
10000
-1,5
-2
Frequência (Hz)
Figura 8
Quando f=f0, tg  =0  X L  X C  0  X L  X C
W0 L 
1
1
1
W 2 
 f0 
W0 C
LC
2
1
LC
f 0  1491Hz
Conclusão:
Verificamos que os pontos obtidos na execução da experiência apresentaram-se próximos
da curva teórica esperada.
Observamos que quanto mais próximo da freqüência f0, os erros foram ampliando, pois
uma pequena variação na freqüência ocasionava uma grande mudança de fase.
Utilizando as curvas de Lissajous, obtivemos o valor de f0, cujo erro está na tabela abaixo:
Frequencia (Hz)
1491
Frequencia Teorica (Hz) Erro Obtido (%)
1516
0,98
.
Verificamos que a freqüência f0 calculada aproximou-se bastante da medida, indicando que
o modelo teórico foi bem elaborado.