movimento_harmonico_simples Lista

Lista de exercícios sobre M.H.S.
Primeira Etapa
1) Um sistema massa-mola oscila sobre um plano horizontal sem atrito
entre as posições -20 cm e + 20 cm, efetuando 20 oscilações completas
em 80 s. Determine:
a) a amplitude do movimento;
b) a freqüência e o período do movimento.
2) Um ponto material oscila com MHS de freqüência 0,50 Hz e amplitude
0,20m. Sabe-se que no instante t = 0 ele passa pela posição x = + 0,20 m.
Determine:
a) a freqüência angular e a fase inicial;
b) a função da posição (ou elongação) em relação ao tempo;
c) a função da velocidade em relação ao tempo;
d) a função da aceleração em relação ao tempo;
e) a posição, a velocidade e a aceleração no instante t = 0,5 s;
f) o módulo da velocidade e da aceleração máxima.
3) A função da posição de um ponto material em MHS, no SI, é x =
0,08.cos0,3t. Determine:
a) a amplitude, a freqüência angular e a fase inicial;
b) a função da velocidade em relação ao tempo;
c) a função da aceleração em relação ao tempo;


4
2
4) Um corpo realiza um MHS regido pela lei horária x  10. cos( . t  ) , no
CGS. Determine:
a) as funções horárias da velocidade e da aceleração;
b) a velocidade e a aceleração do corpo no instante t = 2s.
5) Um ponto material realiza um MHS obedecendo à função horária
x  3. cos( . t 

3
) , no SI. Determine:
a) a amplitude, a pulsação e a fase inicial;
b) o período e a freqüência;
c) a posição do ponto material no instante 2 s.
6) Um móvel executa um MHS cuja amplitude é 5 cm e o período é 2 s.
Determine a velocidade e a aceleração do móvel no instante em que sua
elongação é x = 4 cm.
7) Um ponto material realiza um MHS, tal que sua velocidade máxima é 10
m/s e sua aceleração máxima é 40 m/s2. Determine:
a) amplitude
b) a freqüência do movimento.
8) Um ponto material realiza um MHS cuja função horária da elongação é

x  2. cos( . t ) no SI. Construa os gráficos da elongação, velocidade e
2
aceleração em função do tempo desse movimento.
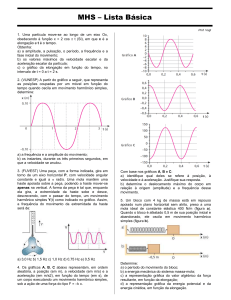
9) A elongação de um ponto material em MHS é dada pelo gráfico a
seguir:
Determine:
a) a amplitude, o período e a freqüência;
b) a pulsação;
c) a função horária da elongação.
10) (UFBA) Uma mola ideal, de constante elástica igual a 16 N/m, tem uma
de suas extremidades fixa e a outra presa a um bloco de massa igual a
4.10-2 kg. O sistema assim constituído passa a executar MHS, de
amplitude 3,5.10-2 m. Determine a velocidade máxima atingida pelo bloco.
Segunda Etapa
1. (UECE) Um sistema massa-mola é preso ao teto. A partir do ponto de equilíbrio
faz-se a massa oscilar com pequena amplitude. Quadruplicando-se o valor da
massa, repete-se o mesmo procedimento. Neste caso, podemos afirmar
corretamente que a freqüência de oscilação
a) é reduzida à metade.
b) dobra.
c) permanece a mesma.
d) quadruplica.
2. (UFMS) A figura 1 representa um sistema mecânico que ilustra o
funcionamento de um motor a combustão, simplificado, com apenas três peças:
virabrequim, biela e pistão. Essas três peças estão acopladas entre si, através de
eixos articulados. Enquanto o virabrequim gira com velocidade angular constante,
no sentido horário, a biela faz o pistão subir e descer num movimento oscilatório.
A posição do pistão no eixo vertical y, é dada pela projeção do ponto de
articulação entre a biela e o pistão sobre esse eixo.
Essa posição no eixo y, oscila entre as amplitudes +A e -A.
Chamemos de y, v Y e a Y , respectivamente, a posição, a velocidade e a aceleração
do ponto de articulação entre a biela e o pistão.
Se iniciarmos a marcação do tempo t, quando a posição do ponto de articulação
entre a biela e o pistão estiver na posição y = 0, como mostra a figura 1, assinale a
alternativa que apresenta corretamente os gráficos correspondentes às posições
y, às velocidades v Y e às acelerações a Y em função do tempo.
3. (UFU) Em um laboratório de Física, um grupo de alunos, Grupo A, obtém dados,
apresentados na tabela a seguir, para a freqüência (em hertz) num experimento
de Pêndulo Simples, utilizando-se três pêndulos diferentes.
Esses resultados foram passados para um segundo grupo, Grupo B, que não
compareceu à aula. Uma vez que os alunos do Grupo B não viram o experimento, os
integrantes desse grupo formularam uma série de hipóteses para interpretar os
resultados. Assinale a ÚNICA hipótese correta.
a) A massa do pêndulo 1 é menor do que a massa do pêndulo 2 que, por sua vez, é
menor do que a massa do pêndulo 3.
b) A massa do pêndulo 1 é maior do que a massa do pêndulo 2 que, por sua vez, é
maior do que a massa do pêndulo 3.
c) O comprimento L do fio do pêndulo 1 é maior do que o comprimento do pêndulo
2 que, por sua vez, é maior do que o comprimento do pêndulo 3.
d) O comprimento L do fio do pêndulo 1 é menor do que o comprimento do pêndulo
2 que, por sua vez, é menor do que o comprimento do pêndulo 3.
4. (UFMS) O Bungee Jump é um esporte radical que consiste na queda de grandes
altitudes de uma pessoa amarrada numa corda elástica. Considerando desprezível
a resistência do ar, é correto afirmar que
(01) a velocidade da pessoa é máxima quando a força elástica da corda é igual à
força peso que atua na pessoa.
(02) a velocidade da pessoa é máxima quando o deslocamento da pessoa, em
relação ao ponto que saltou, é igual ao comprimento da corda sob tensão nula.
(04) o tempo de movimento de queda independe da massa da pessoa.
(08) a altura mínima que a pessoa atinge em relação ao solo depende da massa
dessa pessoa.
(16) a aceleração resultante da pessoa é nula quando ela atinge a posição mais
baixa.
5. (UFRS) Um pêndulo simples, de comprimento L, tem um período de oscilação T,
num determinado local. Para que o período de oscilação passe a valer 2T, no
mesmo local, o comprimento do pêndulo deve ser aumentado em
a) 1 L.
b) 2 L.
c) 3 L.
d) 5 L.
e) 7 L.
6. (UNESP) Uma pequena esfera suspensa por uma mola executa movimento
harmônico simples na direção vertical.
Sempre que o comprimento da mola é máximo, a esfera toca levemente a
superfície de um líquido em um grande recipiente, gerando uma onda que se
propaga com velocidade de 20,0 cm/s. Se a distância entre as cristas da onda for
5,0 cm, a freqüência de oscilação da esfera será
a)0,5Hz. b)1,0Hz. c)2,0Hz. d)2,5Hz. e)4,0Hz.
7. (UEM) Suponha que um pequeno corpo, de massa m, esteja preso na
extremidade de um fio de peso desprezível, cujo comprimento é L, oscilando com
pequena amplitude, em um plano vertical, como mostra a figura a seguir. Esse
dispositivo constitui um pêndulo simples que executa um movimento harmônico
simples. Verifica-se que o corpo, saindo de B, desloca-se até B' e retorna a B, 20
vezes em 10 s. Assinale o que for correto.
(01) O período deste pêndulo é 2,0 s.
(02) A freqüência de oscilação do pêndulo é 0,5 Hz.
(04) Se o comprimento do fio L for 4 vezes maior, o período do pêndulo será
dobrado.
(08) Se a massa do corpo suspenso for triplicada, sua freqüência ficará
multiplicada por 3 .
(16) Se o valor local de g for 4 vezes maior, a freqüência do pêndulo será duas
vezes menor.
(32) Se a amplitude do pêndulo for reduzida à metade, seu período não
modificará.
8. (UNESP) O período de oscilação de um pêndulo simples, que oscila com
amplitude muito pequena, é dado por T= 2
L
, onde Lé o comprimento do pêndulo
g
e g a aceleração da gravidade. Se esse comprimento fosse quadruplicado,
a) o que ocorreria com seu período?
b) o que ocorreria com sua freqüência?
9. (UFRRJ) Dois pêndulos simples, A e B, estão oscilando num mesmo local.
Enquanto A faz uma oscilação em um segundo, B faz duas. Pode-se afirmar, sobre
cada um dos pêndulos, que
a) o comprimento de B é quatro vezes mais curto que o de A.
b) o comprimento de A é quatro vezes mais curto que o de B.
c) os comprimentos de A e de B são iguais, só suas velocidades é que são
diferentes.
d) a massa de A é menor que a massa de B.
e) a massa de B é menor que a massa de A.
10. (MACKENZIE) Um corpo C, de massa 1,00.10 1 kg, está preso a uma mola
helicoidal de massa desprezível e que obedece à Lei de Hooke. Num determinado
instante, o conjunto se encontra em repouso, conforme ilustra a figura 1, quando
então é abandonado e, sem atrito, o corpo passa a oscilar periodicamente em
torno do ponto O. No mesmo intervalo de tempo em que esse corpo vai de A até B,
o pêndulo simples ilustrado na figura 2 realiza uma oscilação completa. Sendo g =
10 m/s², a constante elástica da mola é:
a) 0,25 N/m
b) 0,50 N/m
c) 1,0 N/m
d) 2,0 N/m
e) 4,0 N/m
11. (UFF) Em 1581, na Catedral de Pisa, Galileu teve sua atenção despertada para
um candelabro que oscilava sob a ação do vento, descrevendo arcos de diferentes
tamanhos.
Reproduzindo esse movimento com um pêndulo simples de comprimento L e massa
m, como o representado na figura a seguir, Galileu constatou que o tempo de uma
oscilação pequena (para a qual sen š ¸ š) era função:
a) do comprimento do pêndulo, de sua massa e da aceleração da gravidade
b) apenas do comprimento do pêndulo
c) do comprimento do pêndulo e da aceleração da gravidade
d) apenas da aceleração da gravidade
e) apenas da massa do pêndulo
12. (FUVEST)
Uma peça, com a forma indicada, gira em torno de um eixo horizontal P, com
velocidade angular constante e igual a  rad/s. Uma mola mantém uma haste
apoiada sobre a peça, podendo a haste mover-se APENAS na vertical. A forma da
peça é tal que, enquanto ela gira, a extremidade da haste sobe e desce,
descrevendo, com o passar do tempo, um movimento harmônico simples Y(t) como
indicado no gráfico. Assim, a freqüência do movimento da extremidade da haste
será de
a)3,0Hz b)1,5Hz c)1,0Hz d)0,75Hz e)0,5Hz
13. (MACKENZIE) Um corpo, preso a uma mola conforme figura a seguir, executa
na Terra um M.H.S. de freqüência 30Hz. Levando-se esse sistema à Lua, onde a
aceleração da gravidade é 1/6 da aceleração da gravidade da Terra, a freqüência
do M.H.S. descrito lá é:
a) 5 Hz
b) 10 Hz
c) 30 Hz
d) 60 Hz e) 180 Hz
14. (UEL) Um corpo de massa m é preso à extremidade de uma mola helicoidal que
possui a outra extremidade fixa. O corpo é afastado até o ponto A e, após
abandonado, oscila entre os pontos A e B.
Pode-se afirmar corretamente que a
a) aceleração é nula no ponto 0.
b) a aceleração é nula nos pontos A e B.
c) velocidade é nula no ponto 0.
d) força é nula nos pontos A e B.
e) força é máxima no ponto 0.
15. (FUVEST) Na Terra, certo pêndulo simples executa oscilações com período de
1s.
a) Qual o período desse pêndulo se posto a oscilar na Lua, onde a aceleração da
gravidade é 6 vezes menor?
b) Que aconteceria com o período desse pêndulo à medida que fosse removido
para uma região livre de ações gravitacionais?
GABARITO
01. A
02.
03.
04.
05.
06.
07.
08.
E
D
09 ==> 08 e 01
C
E
36
a) O período dobra.
b) A freqüência reduz-se à metade.
09. B
10. B
11. C
12. B
13. C
14. A
15. a) 2,4s
b) b) remover o pêndulo para uma região livre de ações gravitacionais é
o mesmo que dizer que a aceleração gravitacional tende a zero. Pela equação
do período do pêndulo simples, este período tenderia a infinito.