exercícios modelo gás ideal

FORMAS DE ENERGIA. PRIMEIRA LEI DA TERMODINÂMICA.
EMPREGO DE GASES IDEAIS
Exercício 1:
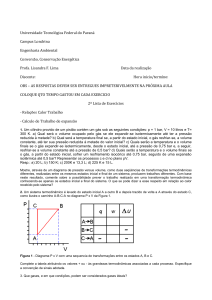
Um gás contido em um conjunto cilindro pistão sofre um ciclo termodinâmico que consiste em
três processos:
1-2: Compressão com PV = Constante de P1 = 1 bar e V1 = 1,0 m3 até V2 = 0,2 m3
2-3: Expansão até V3 = 1,0 m3 em um processo a pressão constante
3-1: Processo a volume constante
Esboce o ciclo em um diagrama P-V atribuindo valores para a pressão e o volume em cada
estágio descrito.
Dicas para solução:
Com a ajuda dos dados e das relações matemáticas que expressa cada processo o aluno deve
colocar o ponto inicial (1), num diagrama P-V, e a partir daí deve construir o diagrama do ciclo.
Exercício 2:
Um arranjo pistão cilindro contém inicialmente 0,4 m 3 de ar a 100 kPa e 80 oC. O ar é então
comprimido até 0,1 m3 de tal maneira que a temperatura dentro do cilindro permanece
constante. Considere que o ar responde plenamente ao modelo de gás ideal, cujo valor de R =
0,287 kJ/kg-K. Feitas essas considerações:
a)Determine o trabalho realizado durante esse processo.
b)Determine a troca de calor entre o ar dentro do conjunto cilindro pistão e a vizinhança
Dicas para solução
O ar em um arranjo pistão cilindro é comprimido isotermicamente. O trabalho de fronteira deve
ser determinado. Como parte da solução, e considerando os dados oferecidos, o aluno deve
desenhar o processo num diagrama P-V.
O ar para o caso pode ser considerado um gás ideal, sendo que para a condição do problema,
(compressão a Temperatura constante), existe uma relação determinada entre a pressão e o
volume que permite a execução da integral para a determinação do trabalho, que pelo fato de
ser um trabalho de compressão é realizado sobre o sistema com as consequências
pertinentes.
Exercício 3:
Um tanque de 20 m3 contém nitrogênio a 23 oC e 600 kPa. Parte do nitrogênio é liberada até
que a pressão do tanque cai para 400 kPa. Se a temperatura nesse ponto for de 20 oC,
determine a quantidade de nitrogênio que foi liberada.
Dicas para solução:
A saída de nitrogênio do tanque obedece a uma válvula ou seu similar instalada no tanque.
Sendo que se trata de nitrogênio o valor de R = 0,2968 kJ/kg – oK. Observe que a queda de
pressão para o caso de fluido compressível está atrelada à queda de temperatura.
Aplicando a equação de estado duas vezes, é possível determinar a massa de nitrogênio antes
e depois de acordo com:
Para posteriormente estabelecer a diferença entre os valores de m.
Exercício 4:
Considere uma mistura gasosa cujo peso molecular aparente é de 33 kg/kmol, inicialmente a 3
bar e 300 oK, ocupando um volume de 0,1 m3. O gás é submetido a uma expansão durante a
qual a relação pressão-volume é PV1,3 = Constante, e o calor transferido para o gás é de 3,84
kJ.
Considerando que a expansão ocorre até que a pressão atinge 1 bar, e que a constante
universal dos gases é 8,3144 kJ/kg-oK, e desprezando os efeitos das energias potencial e
cinética, determine:
a)Temperatura final (oK)
b)O volume final (m3)
c)Trabalho realizado (kJ)
d)Variação de energia interna (kJ)
Dicas para solução:
Antes de dar o primeiro passo na solução do problema, o aluno deve lembrar que existe uma
relação entre a constante universal dos gases ideais e a constante particular (de cada gás ou
mistura de gases), associada ao peso molecular.
Posteriormente, pode ser aplicada a seguinte equação:
)n-1/n
Oferece diretamente o valor da temperatura T2
Posteriormente, aplicando a equação de estado do gás ideal é possível determinar a massa de
gás para o estado inicial, para posteriormente aplicar a mesma equação para o estado final
para determinar o volume final do gás.
Adaptando a solução da integral pdV para o gás ideal (equação mostrada a seguir), é possível
determinar o trabalho (no caso realizado pelo gás), para depois, com a ajuda da equação de
balanço de energia (primeira lei), determinar a variação de energia interna.
Exercício 5:
Para qualquer gás cuja equação de estado seja dada exatamente como pv = RT , a energia
interna depende somente da temperatura. A entalpia específica de um gás, também descrito
por pv = RT também depende somente da temperatura, como pode ser mostrado, pela
combinação da definição de entalpia, h = u + pv, com a energia interna em função da
temperatura.
Tomadas em conjunto, essas especificações constituem o modelo de gás ideal, que representa
estados onde a pressão é pequena em relação à pressão crítica e/ou a temperatura é elevada
em relação à temperatura crítica. É possível admitir com uma precisão aceitável em cálculos de
engenharia que:
Considere ar como gás ideal submetido a uma expansão politrópica em um conjunto cilindro
pistão desde p = 6 bar e 160 oC até a pressão de 1 bar. Empregando o modelo de gás ideal,
determine o trabalho e o calor transferido por unidade de massa durante a expansão.
Represente a expansão do gás num diagrama p-v.
Considere que n = 1,3 para o processo politrópico, e que, o calor específico a volume
constante admitido para os cálculos no intervalo de temperatura é de 0,733 kJ/kg-K, e que a
constante do ar é R = 0,287 kJ/kg-K
Pelo emprego do gás ideal, admita também as seguintes relações:
Exercício 6:
A quantidade de calor transferida num processo depende dos detalhes do mesmo, e não
apenas dos estados inicial e final. Assim, da mesma forma que o trabalho, o calor não é uma
propriedade sendo sua diferencial escrita como δQ.
Assim, considere um gás num conjunto cilindro pistão que passa por um processo de
expansão, cuja relação entre pressão e volume é dada por:
São conhecidas a pressão inicial, de 5 bar, o volume inicial, de 0,1 m3 e o volume final, de 0,2
m3.
Determine o trabalho para o processo em (kJ). Considere que o gás não tem que ter
necessariamente o comportamento de gás ideal.
Exercício 7:
Um gás em um arranjo cilindro – pistão é comprimido, e como resultado disso, sua temperatura
se eleva. É essa uma interação entre sistema e vizinhança de calor ou de trabalho?
Exercício 8:
O manômetro de um tanque de oxigênio de 2,5 m3 indica 500 kPa. Determine a quantidade de
oxigênio no tanque se a temperatura for de 28 oC, e a pressão atmosférica for de 97 kPa.
Considere que a massa molar do oxigênio é de 31,999 kg/kmol, e que o desempenho do
mesmo é o desempenho de um gás ideal.
Exercício 9:
Ar é comprimido adiabaticamente desde P1 = 1 bar, T1 = 300 K, até P2 = 15 bar e v2 = 0,1227
m3/kg. O ar então é resfriado a volume constante até T3 = 300 K. Considerando comportamento
de gás ideal e desprezando os efeitos da energia cinética e potencial, e considerando ainda
que o processo ocorre em equilíbrio; calcule o trabalho para o primeiro processo e a
quantidade de calor transferida no segundo processo em (kJ/kg de ar).
b)Determine o índice n para a condição da compressão, considerando que de fato a
compressão ocorre conforme PVn = Constante
Dicas para solução:
O processo descrito (de compressão de ar) ocorre adiabaticamente, ou seja, sem troca de
calor entre ar e vizinhança, de acordo ao texto do problema, porém, o índice (expoente n) da
relação entre pressão e volume não é descrito, de fato, trata-se da interrogante do item (b)
Portanto, determinando a variação de energia interna do ar em função da temperatura é
possível resolver as interrogantes em ambos os processos, observando que, no resfriamento a
volume constante, até a temperatura inicial, não existe variação de volume, portanto, não
existe nenhuma forma de deslocamento de fronteira.
Soluções a partir da tabela de gases ideais para o ar que se encontram nos livros de texto da
disciplina podem ser aplicadas, assim como a determinação do calor específico médio obtido
em função da temperatura média.
Obtido o trabalho na condição de balanço, é possível encontrar o valor de n da equação de
trabalho.
Exercício 10:
A relação matemática entre pressão e volume em processos de expansão ou compressão
aplicados a sistemas fechados permite modelar em termos da engenharia uma determinada
trajetória que permita a aplicação da integral que relaciona a pressão com o volume e seu
correspondente resultado.
Uma aplicação concreta dessa alternativa foi analisada na pergunta anterior, onde um
processo quase estático em equilíbrio descreveu cada estado da trajetória entre os pontos 1 e
2.
Esses resultados, nem sempre são possíveis na prática, onde vários aspectos contribuem para
a não uniformidade da trajetória do trabalho, não sendo possível a aplicação da integral. Assim,
o que segue, descreve um desses casos.
Um conjunto cilindro pistão contem 2 kg de ar a T = 300 K e P = 1 bar. O ar é comprimido até
que T = 550 K e 6 bar. Durante a compressão a quantidade de calor de 50 kJ é transferida do
ar para a vizinhança. Utilizando o modelo de gás ideal para o ar determine o trabalho
realizado durante o processo em kJ. Na sua análise, considere que o valor do calor
específico a volume constante, avaliado em função da temperatura obedece a seguinte tabela.
Considere que o processo ocorre fora das condições de equilíbrio.
T (K)
300
325
350
375
400
425
450
475
500
525
Cv (kJ/kgK)
0,718
0,7195
0,721
0,7235
0,726
0,7295
0,733
0,7375
0,742
0,7475
11-Um conjunto cilindro pistão contem 2 kg de ar a T = 400 K e P = 1 bar. O ar é comprimido
até que T = 650 K e 6 bar. Durante a compressão a quantidade de calor de 40 kJ é transferida
do ar para a vizinhança. Utilizando o modelo de gás ideal para o ar determine qa trabalho
realizado durante o processo em kJ.
12-O ar é submetido a uma compressão politrópica em um conjunto cilindro pistão onde P1 = 1
bar, T1 = 30 oC para P2 = 5 bar
Utilizando o modelo de gás ideal determine o trabalho e a quantidade de calor transferido por
unidade de massa quando n = 1,3
Represente o processo num diagrama P-V
13-Um conjunto cilindro pistão contem 2 kg de ar a T = 400 K e P = 1 bar. O ar é comprimido
até que T = 650 K e 6 bar. Durante a compressão a quantidade de calor de 40 kJ é transferida
do ar para a vizinhança. Utilizando o modelo de gás ideal para o ar determine qa trabalho
realizado durante o processo em kJ.
14-O ar é submetido a uma compressão politrópica em um conjunto cilindro pistão onde P1 = 1
bar, T1 = 30 oC para P2 = 5 bar
Utilizando o modelo de gás ideal determine o trabalho e a quantidade de calor transferido por
unidade de massa quando n = 1,3
Represente o processo num diagrama P-V
15-UM arranjo cilindro pistão contém inicialmente gás hélio a 150 kPa, 20 oC e 0,5 m3. O hélio
é então comprimido em um processo politrópico (PVn = C), até 400 kPa e 140 oC. Determine a
perda ou ganho de calor durante esse processo.
Considere que, de acordo com as tabelas do hélio R = 2,0769 kJ/kg-K, Cv – 3,1156 kJ/kg-K
Resposta: calor rejeitado Q = -11,055 kJ
16-O ar é comprimido adiabaticamente desde P1 = 1 Bar e T1 = 300 K até P2 = 15 Bar e v2 =
0,1227 m3/kg. O ar é então resfriado a volume constante até T 3 = 300 K. Admitir
comportamento de gás ideal considerando desprezíveis as variações de energia potencial e
cinética.
a)Calcule o trabalho realizado para o primeiro processo (kJ/kg)
b)Calcule a transferência de calor para o segundo processo
Respostas: w = -251,44 kJ/kg; q = -252,43 kJ/kg (calor rejeitado)
17-Um gás é confinado de um lado de um tanque rígido, bem isolado termicamente, dividido
por uma separação. O outro lado está inicialmente em vácuo. Os seguintes dados são
conhecidos para o estado inicial do gás:
P1 = 3 bar; T1 = 380 K; V1 0,025 m3. Quando a separação é interrompida, o gás se expande
para preencher todo o tanque e atinge uma pressão final de equilíbrio de 1,5 bar. Admitindo
comportamento de gás ideal determine o volume final em m3
Resposta: V2 = 0,05 m3
18-Um tanque rígido com volume 0,057 m3 contém ar inicialmente a 13,8 kPa e 200 oC. Se o ar
recebe uma transferência de calor de 6,5 kJ, determine a temperatura final e a pressão final
admitindo comportamento de gás ideal