exp_23_iemec - Prof. Selmo Bernardo Torquetto

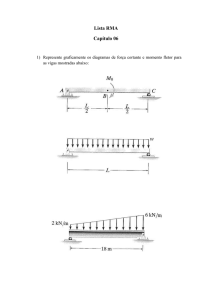
EXPERIMENTO N 23: Alavancas: Interfixa; Interpotente e Inter-resistente
Engenharia Mecânica – Disciplina de Introdução à Engenharia - IEMEC
Objetivos: O experimento realizado permite avaliar os tipos de alavancas usadas
em diversas áreas da engenharia.
Histórico: Arquimedes de Siracusa (Grécia, Siracusa, 287 a.C. – 212 a.C.) foi
um matemático, físico, engenheiro, inventor, e astrônomo grego. Embora poucos
detalhes de sua vida sejam conhecidos, ele é considerado um dos principais
cientistas da Antiguidade Clássica.
Fig.1 Pintura de Domenico Fetti (1620)
Entre suas contribuições a Física, está a fundação da hidrostática e da estática,
tendo descoberto a lei do empuxo e a lei da alavanca, além de muitas outras. Ele
inventou ainda vários tipos de máquinas para uso militar e civil, incluindo armas de
cerco, e a bomba de parafuso que leva seu nome. Experimentos modernos
testaram alegações de que, para defender sua cidade, Arquimedes projetou
máquinas capazes de levantar navios inimigos para fora da água e colocar navios
em chamas usando um conjunto de espelhos.
Arquimedes é geralmente considerado o maior matemático da antiguidade, e um
dos maiores de todos os tempos.Ele usou o método da exaustão para calcular a
área sob o arco de uma parábola utilizando a soma de uma série infinita, e
também encontrou uma aproximação bastante acurada do número π. Também
descobriu a espiral que leva seu nome, fórmulas para os volumes de superfícies
de revolução e um engenhoso sistema para expressar números muito grandes.
Durante o cerco a Siracusa, Arquimedes foi morto por um soldado romano,
mesmo após os soldados terem recebido ordens para que não o ferissem, devido
a admiração que os líderes romanos tinham por ele. Anos depois, Cícero
descreveu sua visita ao túmulo de Arquimedes, que era encimado por uma esfera
inscrita em um cilindro. Arquimedes tinha provado que a esfera tem dois terços do
volume e da área da superfície do cilindro (incluindo as bases da última), e
considerou essa como a maior de suas realizações matemáticas.
Frase de Arquimedes: “Dê-me uma alavanca e um ponto de apoio e levantarei o
mundo”
Fig.2 Atlas levantando o mundo
Introdução Teórica:
Alavanca: É um objeto rígido que é usado com um ponto fixo apropriado (fulcro
ou ponto de apóio) para multiplicar a força mecânica que pode ser aplicada a um
outro objeto (resistência). Sendo também denominado como vantagem mecânica,
e é um exemplo do princípio dos momentos conforme ilustrado na Fig.3 abaixo:
Fig.3 Exemplo clássico de alavanca
A força aplicada em pontos de extremidade da alavanca é proporcional à relação
do comprimento do braço de alavanca medido entre o ponto de apoio e o ponto da
aplicação da força aplicada em cada extremidade da alavanca.
Usando-se o princípio dos momentos a equação fundamental das alavancas é:
Adotando-se momento positivo para giro no sentido horário e negativo para o
sentido anti-horário temos:
 M = 0 , ou seja:
- F1 x D1 + F2 x D2 = 0, então temos:
F2 x D2 = F1 x D1
onde:




F1 é a força potente;
F2 é a força resistente;
D1 é o braço potente;
D2 é o braço resistente.
Tipos de Alavancas:
Interfixa: O de apoio (PA) fica entre a força resistente (R) e a força potência (P)
P x BP = R x BR, ou ainda:
R = P x BP / BR
Fig.4 Alavanca interfixa
Interpotente: A força potência (P) fica entre o ponto da aplicação da força
resistente (R) e o ponto de apóio (PA).
Fig.5 Alavanca interpotente
Inter- resistente: A força resistente ( R ) fica entre o ponto de apoio (PA) e a
aplicação da força potencia (P).
Fig.6 Alavanca inter-resitente
Aplicações de alavancas:
Fig.7 Aplicações de alavancas
Material para o experimento:
a)
b)
c)
d)
e)
f)
g)
h)
2 copos descartáveis de 200 ml
2 copos descartáveis de 50 ml
1 garrafa PET de 1,5 L
1 régua de madeira de 300 mm
1 pedaço de madeira (compensado) de 4mm x 25 mm x 300 mm
1 furador
500 mm de barbante
200mm de arame galvanizado de diâmetro de 1 mm
Roteiro de Montagem:
Primeira Parte: Alavanca Interfixa
a) Pegar o pedaço de madeira de 4 mm x 25 mm x 300 mm e fazer um furo
com o furador a 20 mm de uma extremidade e outro furo a 20 mm na outra
extermidade da mesma e finalmente um terceiro furo a partir da
extremidade da esquerda distante de 100mm.
b) Fazer um olhal de arame galvanizado para colocar no terceiro furo feito na
madeira de 4 mm x 25 mm x 300 mm
c) Fazer dois cestos com o barbante e com os dois copos descartáveis de 200
ml
d) Prender ambos os cestos de 200 ml em cada extremidade da madeira
e) Fixar o conjunto através do olhal de arame galvanizado em um pé da
cadeira colocada sobre uma mesa.
f) Colocar no copo à esquerda 2 copos de 50 ml
g) Colocar no copo à direita a quantidade de àgua até o equilíbrio dos copos.
h) Anotar os valores de água colocados em cada copo de 200 ml e comprovar
atravéz de cálculo para ccomprovar os resultados para elaborar o relatório
final do experimento.
Segunda Parte: Alavanca Interpotente
a)Adaptar o roteiro do experimento anterior para a segunda parte “ Alavanca
Interpotente”
Terceira Parte: Alavanca Inter-resistente
a)Idem ao roteiro do experimento anterior para a terceira parte “ Alavanca
Inter-resitente”
Fonte Bibliográfica:
a) http://pt.wikipedia.org/wiki/Alavanca
b) http://pt.wikipedia.org/wiki/Arquimedes
c) http://www.feiradeciencias.com.br/sala06/06_RE02.asp