Estática. A força e o momento da força. O equilíbrio de forças

Capítulo 5
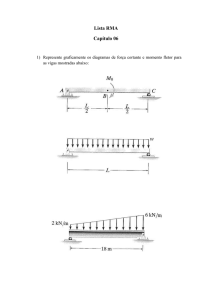
Mecânica
Parte da Física que estuda o comportamento de sistemas físicos sujeitos a forças.
5.1
Estática
Ramo da mecânica que estuda as forças actuantes num sistema mecânico em equilíbrio (todos os pontos
do sistema têm uma velocidade relativa nula).
Vejamos o exemplo da figura 5.1. As duas forças actuantes sobre o corpo anulam-se: têm igual
intensidade e direcção mas sentidos contrários. Em linguagem matemática, a soma dos dois vectores é
um vector nulo.
Figura 5.1: Exemplo de equilíbrio estático
É intuitivo qual é a primeira condição de equilíbrio estático para um sistema mecânico. É necessário
que a soma de todas as forças actuantes no sistema seja nula:
N
X
F~i = ~0
(5.1)
i=1
Mas será suficiente? Vejamos o exemplo da figura 5.2. Apesar da condição 5.1 verificar-se, não
haverá equiliíbrio estático. Na verdade o corpo da figura vai rodar em torno de um ponto.
Figura 5.2: Exemplo de ausência de equilíbrio estático
A condição 5.1 assegura apenas que não haverá um movimento de translação do corpo.
Para que não haja rotação é necessário não só ter em conta as forças aplicadas mas também os
pontos onde são aplicadas. A grandeza física que conjuga estes dois dados (força e posição de aplicação)
~ e é definida como:
chama-se N
~ = ~r ⇥ F~
N
em que ~r é o vector posição do ponto de aplicação da força F~ .
21
(5.2)
5.1. ESTÁTICA
CAPÍTULO 5. MECÂNICA
O símbolo ⇥ representa um produto externo; é um produto vectorial especial do qual resulta um
novo vector que será diferente de zero quando ~r e F~ não tiverem a mesma direcção.
~ i será dada por:
Se ↵ é o ângulo entre ~ri e F~i então a intensidade do binário N
~ i = ||~ri || F~i sin ↵
N
Quando ↵ = 0 ou ↵ = ⇡ o momento da força será nulo.
Se o momento de uma força for diferente de zero então irá contribuír para que ocorra um movimento
de rotação do sistema. Desta afirmação resulta a segunda condição de equilíbrio estático para um
sistema mecânico. É necessário que a soma de todos os momentos de força actuantes no sistema seja
nula:
N
X
~ i = ~0
N
(5.3)
i=1
Em resumo, aprimeira condição assegura que não ocorrerá translação e a segunda que não ocorrerá
rotação.
Como informação suplementar, chama-se binário a um conjunto de duas forças de igual intensidade
e direcção mas sentido contrário aplicadas em pontos distintos.
5.1.1
Alavanca
Uma alavanca é um sistema mecânico (uma das 6 máquinas simples) formado por uma barra rígida
confinada a mover-se rodando em torno de um ponto ou de uma linha (o fulcro f - ver a figura 5.3).
f
FP
FR
Figura 5.3: Alavanca
É actuada por duas forças: a força potente (F~P ) e a força resistente (F~R ). A primeira é a força
que promove o movimento (e.g. força gerada por uma músculo) e a segunda é uma força que se opõe
ao movimento (e.g. força gravítica).
Para que exista equilíbrio estático numa alavanca é necessário que se verifiquem as duas condições
de equilíbrio estático (equações 5.1 e 5.3).
No caso da alavanca as 3 forças em jogo são a força potente, a força resistente e a reacção normal
no fulcro e assume-se que a soma destas forças é sempre nula.
Resta então a segunda condição: Se chamarmos braço da força potente (rP ) à distância do fulcro
até ao ponto de aplicação da força potente e braço da força resistente (rR ) à distância do fulcro até
ao ponto de aplicação da força resistente, então a condição da equação5.3 tomará a seguinte forma:
r P FP = r R FR
(5.4)
A força potente necessária para superar o efeito da força resistente será dada por:
FP =
rR
FR
rP
A razão M = rrPR chama-se vantagem mecânica da alavanca. No caso da figura 5.3 a vantagem
mecânica é superior a 1 (porque rP > rR ) e por isso a força potente é inferior à força resistente.
No corpo humano a vantagem mecânica nem sempre é superior a 1. Porquê? Na tabela abaixo
apresenta-se um sumário dos prós e contras de uma vantagem mecânica superior a 1:
22
CAPÍTULO 5. MECÂNICA
5.1. ESTÁTICA
Prós
Menor esforço muscular
Menor tensão nos tendões
Contras
Menor amplitude de movimento da carga
Menor velocidade de movimento da carga
Menor eficiência muscular
Maior variação do comprimento muscular
Tabela 5.1: Tabela de vantagem mecânica superior a 1
A conclusão que se pode tirar é que uma alavanca amplifica uma força quando a vantagem mecânica
é superior a 1 ou amplifica o movimento (amplitude e velocidade) quando a vantagem mecânica é inferior
a 1.
5.1.1.1
Interfixa ou de classe 1
Uma alavanca é interfixa (ou de classe 1) quando o fulcro está entre a força potente e a força resistente.
Figura 5.4: O músculo tríceps
Este tipo de alavanca é o menos comum no corpo humano. A sua vantagem mecânica pode assumir
tanto valores superiores como valores inferiores à unidade (o braço da força potente pode ser maior ou
menor que o braço da força resistente).
5.1.1.2
Inter-resistente ou de classe 2
Uma alavanca é inter-resistente (ou de classe 2) quando a força resistente está entre o fulcro e a força
potente.
Figura 5.5: O músculo braquiorradial
Este tipo de alavanca é o segundo mais comum no corpo humano. A sua vantagem mecânica é
sempre superior à unidade (o braço da força potente é sempre maior que o braço da força resistente).
23
5.2. DINÂMICA
5.1.1.3
CAPÍTULO 5. MECÂNICA
Interpotente ou de classe 3
Uma alavanca é interpotente (ou de classe 3) quando força potente está entre o fulcro e a força
resistente.
Figura 5.6: O músculo bíceps
Este tipo de alavanca é de longe o mais comum no corpo humano. A sua vantagem mecânica é
sempre inferior à unidade (o braço da força potente é sempre menor que o braço da força resistente).
Logo nestas alavancas os músculos são obrigados a exercer grandes forças.
Então porque é que existem tantas alavancas de classe 3 no corpo humano?
• Os músculos estão construídos de forma a suportar grandes cargas (cerca de 70 N cm
2
[3]).
• O deslocamento que são capazes de produzir é pequeno em relação ao seu tamanho. Por exemplo,
um músculo bíceps com 25 cm de comprimento consegue diminuir de tamanho (quando contrai)
cerca de 7 cm (28%) [4]. Numa alavanca do tipo 3 perdemos na vantagem mecânica mas
ganhamos na amplitude de movimento (aumenta por um factor igual ao inverso da vantagem
mecânica).
• O corpo humano está desenhado para o movimento em detrimento da força. Os membros são
longos e por isso favorecem uma grande amplitude de movimentos. Na natureza, os animais que
têm mais força têm membros relativamente curtos.
5.2
Dinâmica
Parte da mecânica onde se estuda o movimento dos corpos assim como as forças que causaram esse
movimento.
Na mecânica clássica, a dinâmica rége-se pelas 3 leis de Newton.
5.2.1
Primeira lei de Newton (Lei da inércia)
Um corpo permanece no estado de movimento uniforme ou parado desde que não actuem forças sobre
ele.
Alguns exemplos:
• Quando um automóvel arranca (figura 5.7a) sentimos uma força que nos impele para trás. Na
realidade o que estamos a sentir é a oposição do nosso corpo à mudança de velocidade a que está
a ser sujeito. O nosso corpo está a tentar manter-se no estado original (parado). De igual modo
quando circulamos num automóvel a velocidade constante, ao travarmos (figura 5.7b) sentimonos impelidos para a frente. O nosso corpo tenta manter o movimento uniforme inicial. Esta
resistência à mudança chama-se inércia.
24
Bibliografia
[1] Almeida, G. d. Sistema Internacional de Unidades (SI), grandezas e unidades físicas (Plátano
editora, S. A., 2002), 3 edn.
[2] (2010). URL http://www.bipm.org/en/si/.
[3] Davidovits, P. Physics in biology and medicine (Elsevier, 2008), 3 edn.
[4] Herman, I. P. Physics of the human body (Springer-Verlag Berlin, 2007), 1 edn.
35