Algarismos Significativos

Fis. Exp. 2 – 2008/1
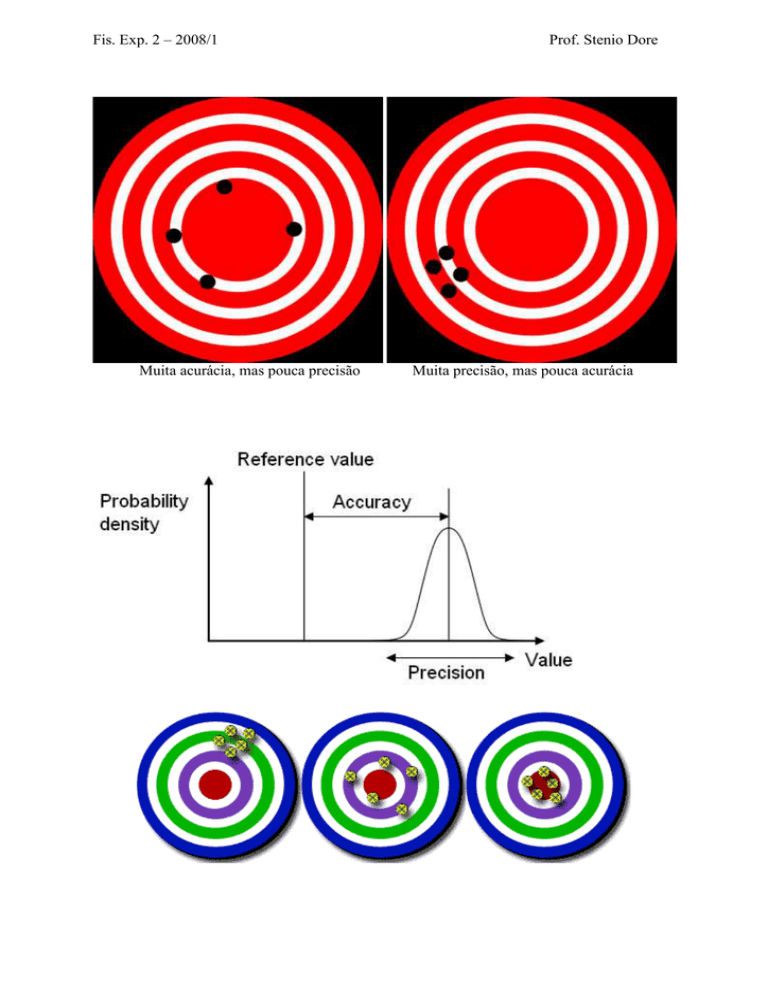
Muita acurácia, mas pouca precisão
Prof. Stenio Dore
Muita precisão, mas pouca acurácia
Algarismos Significativos
O número de algarismos significativos no resultado de um cálculo depende do número de algarismos
significativos nos dados de entrada. Algarismos diferentes de zero sempre são significativos. Assim, 22 tem dois
algarismos significativos . Para zeros é mais complicado:
a.
Zeros colocados antes de outros algarismos não são significativos; 0,046 tem dois algarismos
significativos.
b.
Zeros colocados entre outros algarismos são sempre significativos; 4009 kg tem quatro algarismos
significativos.
c.
Zeros colocados após outros algarismos, mas depois da vírgula decimal, são significativos; 7,90 tem
três algarismos significativos.
d.
Zeros ao final de um número são significativos somente se vierem depois da vírgula decimal como em
(c). Caso contrário é impossível determinar se eles são significativos. Por exemplo, no número 8200
não é claro se os zeros são significativos ou não. O número de algarismos significativos em 8200 é de
pelo menos dois, mas poderia ser três ou quatro. Para evitar esse tipo de dúvida, recorre-se à notação
científica, de modo a que os zeros significativos sempre venham depois da vírgula decimal:
8,200 x 103 tem quatro algarismos significativos
8,20 x 103 tem três algarismos significativos
8,2 x 103 tem dois algarismos significativos
Algarismos significativos na multiplicação, divisão, funções trigonométricas, etc. Num cálculo envolvendo
multiplicação, divisão, funções trigonométricas, etc., o número de algarismos significativos na resposta deve ser
igual ao menor número de algarismos significativos existentes em qualquer um dos números que está sendo
multiplicado, dividido, etc. Assim, ao calcular sen(kx), onde k= 0,097 m-1 (dois algarismos significativos) e x=
4,73 m (três algarismos significativos), a resposta deve ter dois algarismos significativos.
Note que números inteiros têm essencialmente um número ilimitado de algarismos significativos . Por exemplo,
se um motor tem 1,2 kW de potência, então dois deles terão 2,4 kW:1,2 kW (dois algarismos significativos) x 2
(ilimitados algarismos significativos) = 2,4 kW (dois algarismos significativos). O mesmo vale para constantes
como , e, etc.
Algarismos significativos na adição e subtração
Quando quantidades são adicionadas ou subtraídas, o número de casas decimais (e não de algarismos
significativos ) na resposta deve ser o mesmo que o do número que tiver o menor número de casas decimais.
Exemplo:
5,67 J (duas casas decimais)
1,1 J (uma casa decimal)
0,9378 J (quatro casas decimais)
7,7 J (uma casa decimal)
Mantenha um algarismo extra nos resultados intermediários Quando efetuar cálculos em múltiplas etapas,
mantenha pelo menos um algarismo significativo a mais nos resultados intermediários do que o necessário na
resposta final. Por exemplo, se a resposta final requer dois algarismos significativos, mantenha pelo menos três
algarismos significativos nos cálculos intermediários. Se você arredondar todos os seus resultados
intermediários para dois algarismos significativos, você estará em cada passo desprezando informação numérica
contida no terceiro algarismo, como resultado o segundo algarismo da sua resposta final estará incorreto. (Isso
se denomina erro de arredondamento).
Dois erros no uso dos algarismos significativos 1.Escrever mais algarismos na resposta que o justificado pelo
número de algarismos significativos nos dados. 2.Arredondar demais nos resultados intermediários
Teste sua habilidade em reconhecer algarismos significativos com esse joguinho:
http://www.lon-capa.org/~mmp/applist/sigfig/sig.htm