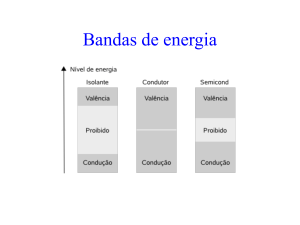
Semicondutores
CF086 - Introdução a Física do Estado Sólido 1
Introdução
Vimos que um dado sólido pode apresentar bandas de energia, que
podem estar totalmente vazias, totalmente preenchidas ou
parcialmente preenchidas.
2
Introdução
Isolante em 𝑇 = 0: bandas vazias ou totalmente preenchidas. A última
banda preenchida num isolante está separada da banda vazia
imediatamente superior por um gap.
Num isolante, o gap é alto (∼> 3 eV) e a resistividade elétrica
também (𝜚 ∼ 1020 Ω ⋅ m).
3
Introdução
Para gaps da ordem de alguns décimos de eV até ∼ 3 eV, temos
semicondutores. As resistividades são menores (𝜚 ∼ 10−5 − 107 Ω ⋅
m) (para metais, 𝜚 ∼ 10−8 Ω ⋅ m).
4
Introdução
Por causa do gap menor, quando 𝑇 ≠ 0 há uma probabilidade de
ocupação dos estados maior, de modo que os elétrons que
“atravessam” o gap é um pouco maior ⇒ material conduz para 𝑇 ≠ 0.
5
Introdução
Outra grandeza importante é a densidade
de portadores.
Vamos comparar os comportamentos
para isolantes e condutores.
6
Introdução
Densidade de estados para elétrons livres (3D):
2𝑚
𝒟 𝜖 =
ℏ2
3
2
𝑉 1
𝜖2
2
4𝜋
𝒟(𝜖) fornece o número de estados, mas não diz se ele está ocupado.
Distribuição de Fermi-Dirac
𝑓 𝜖 =
1
𝑒𝛽
𝜖−𝜇
+1
𝑓 𝜖, 𝑇 = 0 =
1,
0,
𝜖<𝜇
𝜖>𝜇
7
Introdução
Número médio de elétrons: 𝒟 𝜖 𝑓(𝜖).
Em metais, 𝑇 = 0: banda
semipreenchida.
Os níveis são preenchidos até uma
energia máxima: energia de Fermi
𝐸𝐹 .
8
Introdução
Quando 𝑇 ≠ 0: 𝒟(𝜖) é o mesmo, mas
𝑓(𝜖) muda em torno de 𝐸𝐹 = 𝜇(𝑇 =
0), na faixa ±2𝑘𝐵 𝑇 em torno de 𝐸𝐹 .
Os elétrons excitados termicamente
dão origem à corrente elétrica.
Para metais, ocorre excitação em
qualquer 𝑇. Estimativa do número
relativo de elétrons: Δ𝑁𝑇 /𝑁 ∼ 1 %
(𝑇 = 300 K, quadro).
9
Semicondutores
A ideia é similar para semicondutores e isolantes. As bandas são
separadas por um gap.
Última banda preenchida: banda de valência (BV).
Banda vazia superior à BV: banda de condução (BC).
Diferença entre o topo da BV e a base da BC: gap 𝐸𝑔 .
10
Semicondutores
Potencial químico 𝜇(𝑇), ou nível de Fermi: próximo ao meio do gap,
varia pouco com 𝑇 (veremos depois).
𝜇(𝑇) regula o fluxo de
partículas (Termodinâmica).
𝒟 𝜖 = 0 no gap. Não é dada
1
2
apenas por 𝒟 𝜖 ∝ 𝜖 .
11
Semicondutores
Para 𝑇 = 0, 𝑓 𝜖 = 0 se 𝜖 > 𝜇(0).
Logo, 𝑓 𝜖 = 0 para 𝜖 > 𝐸𝑔 .
Não há elétrons de condução.
Para 𝑇 > 0, 𝑓(𝜖) permite alguns
elétrons na BC.
Estimativa (𝑇 = 300 K, quadro):
Δ𝑁/𝑁 ∼ 10−52 , 𝐸𝑔 = 6 eV. Δ𝑁/𝑁 ∼
10−9 , 𝐸𝑔 = 1 eV.
12
Semicondutores
Note que, quando 𝑇 cresce, o número de elétrons excitados
termicamente cresce, e a condutividade aumenta.
Esse comportamento é oposto ao exibido por metais, onde 𝜚 cresce
com 𝑇 (e a condutividade decresce). Em metais,
𝜎met
𝑒2 𝑁
=
𝜏
𝑚 𝑉 𝑒𝑙
e 𝜏𝑒𝑙 diminui com 𝑇, pois há mais colisões.
Semicondutores têm coeficientes de temperatura para a resistividade
negativos ⇒ propriedade que os fez se destacarem no séc. XIX.
13
Semicondutores
A excitação térmica pode fazer com que elétrons passem da BV para a
BC. Essa é a origem da condutividade intrínseca do semicondutor.
Semicondutor intrínseco: condutividade é dominada por efeitos
térmicos.
14
Semicondutores
Ao excitar um elétron da BV para a BC, a BV fica com a ausência de
um elétron.
A BV estava totalmente preenchida. Assim, o momento total dela era
nulo. Não há movimento ordenado de cargas ao aplicar um campo
elétrico fraco (𝐸campo ≪ 𝑘𝐵 𝑇).
Com um elétron a menos, o momento total deixa de ser nulo, e tornase possível alterar estados eletrônicos na BV.
15
Semicondutores
A ausência de um elétron se comporta como uma carga positiva,
chamada “buraco”.
O buraco tem carga oposta à do elétron.
Elétrons no topo da BV têm massas efetivas negativas, pois a BV é
côncava para baixo.
Ausência dos elétrons (buracos) têm massas efetivas positivas.
16
Semicondutores
Ao aplicar um campo elétrico sobre os buracos, eles se comportam de
maneira “normal” ⇒ movem-se no mesmo sentido que o campo.
Há outros modos de alterar a condutividade, além do térmico.
Incidindo radiação com energia da ordem do gap ou maior, os elétrons
da BV podem ser fotoexcitados ⇒ fotocondutividade.
Semicondutores podem ser usados como fotodetectores.
17
Semicondutores
Há outro modo de alterar a condutividade ⇒ impurezas.
Suponha que uma pequena quantidade de arsênio (As) seja
introduzida na rede de germânio (Ge).
18
Semicondutores
Ge: tetravalente, As: pentavalente.
Ao trocar Ge ⇒ As, o As faz 4 ligações com o Ge, e um elétron fica
“flutuando” em torno do As.
O As se comporta como um núcleo com uma carga positiva +𝑒,
envolto por um elétron “orbitando” esse núcleo ⇒ átomo de
hidrogênio, com níveis discretos dentro do gap.
Há algumas diferenças.
19
Semicondutores
O meio blinda a força elétrica ⇒ permissividade elétrica 𝜖, e não 𝜖0 .
Permissividade elétrica relativa 𝜖𝑟 .
A massa do elétron é substituída pela massa efetiva 𝑚∗ .
1
𝐸𝑛𝑑 = −
4𝜋𝜖
2
𝑚∗ 𝑒 4
𝑚∗ 𝐻
=
𝐸
2ℏ2 𝑛2 𝑚𝜖𝑟2 𝑛
Estimativa: 𝐸1𝑑 ∼ 0,01 eV, para 𝑚∗ = 0,2𝑚, 𝜖𝑟 = 16.
20
Semicondutores
O pequeno valor da energia dos níveis doadores faz com que seja fácil
excitar termicamente os portadores para a BC.
Os níveis doadores ficam logo abaixo da BC, no nível 𝐸𝑑 , abaixo de
𝐸𝑐 . As é uma impureza doadora.
21
Semicondutores
Considere a substituição de um Ge por um gálio (Ga).
Ga: trivalente.
A ideia é similar, mas agora temos falta de um elétron, e não excesso.
Há um núcleo de carga −𝑒 e um buraco orbitando esse núcleo.
A situação é simétrica, mas os níveis são próximos à BV.
22
Semicondutores
Os níveis são níveis de buracos. Assim, elétrons podem passar da BV
para estes níveis aceitadores (de elétrons) por excitação térmica.
Surge um nível aceitador 𝐸𝑎 logo acima de 𝐸𝑣 da BV.
23
Semicondutores
Quando elétrons passam da BV para um nível aceitador 𝐸𝑎 , geram
buracos na BV, que podem conduzir.
Ga: impureza aceitadora.
Semicondutor tipo 𝑛 (negativo): níveis doadores.
Semicondutor tipo 𝑝 (positivo): níveis aceitadores.
24
Semicondutores
Representação gráfica:
Semicondutor extrínseco: semicondutor dopado.
25
Semicondutores
Num semicondutor intrínseco (não dopado), o número de estados vazios
na BV é igual ao número de elétrons na BC.
𝜇 (nível de Fermi) fica próximo ao centro do gap.
Bandas simétricas:
𝜇 𝑇 = 0 = 𝐸𝑣 +
𝐸𝑔
2
26
Semicondutores
Semicondutor extrínseco: situação mais complicada.
Semicondutor tipo 𝑛: em 𝑇 = 0, 𝜇 fica entre 𝐸𝑑 e 𝐸𝑐 . Quando 𝑇
cresce, elétrons passam de 𝐸𝑑 para 𝐸𝑐 , e 𝜇 cai.
Quando metade dos elétrons passa de 𝐸𝑑 para 𝐸𝑐 , 𝜇 = 𝐸𝑑 .
Aumentando 𝑇, elétrons da BV passam para a BC, e 𝜇 cai ainda mais,
indo em direção a 𝐸𝑣 + 𝐸𝑔 /2.
27
Semicondutores
Semicondutor tipo 𝑝: em 𝑇 = 0, 𝜇 fica entre 𝐸𝑣 e 𝐸𝑎 . Quando 𝑇
cresce, buracos passam de 𝐸𝑑 para 𝐸𝑣 , e 𝜇 cresce, indo em direção a
𝐸𝑣 + 𝐸𝑔 /2, de forma similar ao que ocorre no tipo 𝑛.
28
Semicondutores
O próprio gap varia com 𝑇:
As dimensões da rede se alteram, e, com isso, as bandas e os intervalos entre
elas também mudam.
A distribuição de fônons varia com 𝑇, e isso influi nas bandas.
29
Semicondutores
Há dois tipos de gaps:
Gap direto: mínimo da BC e máximo da BV ocorrem para o mesmo valor de
𝑘. Assim, eles estão verticalmente alinhados num gráfico ℰ × 𝑘.
Note que o momento transferido
pelo fóton é muito pequeno quando
comparado com o do elétron.
Os vetores 𝑘 para o elétron antes e
depois da transição são iguais.
30
Semicondutores
Gap indireto: mínimo da BC e máximo da BV ocorrem para valores diferentes
de 𝑘.
Para haver conservação de momento, um fônon deve participar da transição.
O fônon pode ser absorvido + ou criado − .
𝐸𝑔 = ℏ𝜔 ± ℏΩ
𝑘𝑐 = 𝑘𝑖 + 𝑞
31
Semicondutores
Os níveis de energia importantes em transições eletrônicas são os que
ficam próximos ao topo da BV e na base da BC.
De forma genérica, estas bandas pode ser escritas como
ℏ2
ℰ 𝑘 = ℰ𝑐 +
2
ℏ2
ℰ 𝑘 = ℰ𝑣 −
2
𝑘𝜇 𝑀−1 𝑘𝜈
,
elétrons
𝑘𝜇 𝑀−1 𝑘𝜈
,
buracos
𝜇𝜈
𝜇𝜈
32
Semicondutores
ℰ𝑐 : base da BC, ℰ𝑣 : topo da BV.
𝑀: tensor de massa efetiva. Na forma diagonal, temos
ℰ 𝑘 = ℰ𝑐 + ℏ2
𝑘12
𝑘22
𝑘32
+
+
2𝑚1 2𝑚2 2𝑚3
,
elétrons
ℏ2
𝑘12
𝑘22
𝑘32
+
+
2𝑚1 2𝑚2 2𝑚3
,
buracos
ℰ 𝑘 = ℰ𝑐 −
As bandas são elipsoides de energia constante (em 𝑘).
33
Semicondutores
Si: 6 bandas de condução em ⟨1 0 0⟩.
Bandas de valência degeneradas em 𝑘 = 0.
34
Semicondutores
Ge
35
Propriedades dos Buracos
Buracos: carga oposta à do elétron.
Vetor de onda do elétron: 𝑘𝑒 . Vetor de onda do buraco (hole):
𝑘ℎ = −𝑘𝑒
Nível de energia zero no topo da BV. Elétrons nela têm energias
negativas. Assim, a energia do buraco é
𝜖ℎ 𝑘ℎ = −𝜖𝑒 𝑘𝑒
36
Propriedades dos Buracos
Velocidade do buraco:
𝑣ℎ = 𝑣𝑒 ⇒ 𝛻ℎ 𝜖ℎ 𝑘ℎ = 𝛻𝑒 𝜖𝑒 𝑘𝑒
Massa efetiva:
𝑚ℎ∗ = −𝑚𝑒∗
Equação de movimento sob campo eletromagnético:
ℏ
𝑑𝑘ℎ
= 𝑒 𝐸 + 𝑣ℎ × ℬ
𝑑𝑡
37
Propriedades dos Buracos
Densidade de corrente:
elétrons na BC: 𝐽𝑒
buracos na BV: 𝐽ℎ
as duas orientam-se no mesmo sentido
Notar que
𝐽 = 𝜎𝐸
𝐽 = 𝜚𝑣
𝜚=
𝑁
𝑄 = 𝑛𝑄
𝑉
𝑄 = ±𝑒
É importante poder determinar 𝑛 ⇒ efeito Hall.
38
Efeito Hall
Na presença de um campo magnético, temos
𝐽 =𝜎 ℬ ⋅𝐸
ou, reescrevendo,
𝐸 =𝑟 ℬ ⋅𝐽
𝑟: tensor resistividade elétrica
𝑟𝑖𝑗 = 𝜎 −1
𝑖𝑗
39
Efeito Hall
Para determinar 𝑟𝑖𝑗 , usa-se a configuração abaixo, chamada
configuração padrão.
40
Efeito Hall
Na situação estacionária 𝐽𝑦 = 0. Assim,
𝑟𝑥𝑥
𝐸𝑥
=
𝑟𝑦𝑥
𝐸𝑦
𝑟𝑥𝑦
𝑟𝑦𝑦
𝐽𝑥
0
Desenvolvendo,
𝐸𝑥 = 𝑟𝑥𝑥 ℬ 𝐽𝑥 ,
𝐸𝑦 = 𝑟𝑦𝑥 ℬ 𝐽𝑥
Magnetoresistividade longitudinal:
𝑟𝑥𝑥 ℬ =
𝐸𝑥
𝐽𝑥
41
Efeito Hall
Magnetoresistividade transversal (resistividade Hall):
𝑟𝑦𝑥
𝐸𝑦
ℬ =
𝐽𝑥
Coeficiente Hall:
𝑟𝑦𝑥
𝐸𝑦
𝑅𝐻 =
=
ℬ
𝐽𝑥 ℬ
Tensão Hall:
𝑉𝐻 = 𝑌𝐸𝑦
42
Efeito Hall
Modelo 1:
um tipo de portador (elétrons), banda isotrópica, densidade numérica 𝑛 e
massa efetiva 𝑚∗ .
meio dissipativo: modelado por um tempo de relaxação 𝜏.
Equação de movimento:
∗
𝑑
𝑣
𝑚
𝑚∗
= −𝑒𝐸 − 𝑒𝑣 × ℬ −
𝑣
𝑑𝑡
𝜏
43
Efeito Hall
Situação estacionária:
𝑑𝑣
𝑑𝑡
=0
𝑣=−
𝑒𝜏
𝑒𝜏
𝐸
−
𝑣×ℬ
𝑚∗
𝑚∗
Frequência cíclotron:
𝜔𝑐 =
𝑒ℬ
𝑚∗
44
Efeito Hall
Desenvolvendo, chega-se a (quadro):
𝑛𝑒 2 𝜏 𝐸𝑥 − 𝜔𝑐 𝜏𝐸𝑦
𝐽𝑥 =
𝑚∗ 1 + 𝜔𝑐2 𝜏 2
𝑛𝑒 2 𝜏 𝜔𝑐 𝜏𝐸𝑥 + 𝐸𝑦
𝐽𝑦 =
𝑚∗ 1 + 𝜔𝑐2 𝜏 2
Então:
𝑚∗
1
𝑟 ℬ = 2
𝑛𝑒 𝜏 −𝜔𝑐 𝜏
𝜔𝑐 𝜏
1
45
Efeito Hall
Magnetoresistividade longitudinal:
𝑟𝑥𝑥
𝑚∗
= 2
𝑛𝑒 𝜏
Magnetoresistividade transversal:
𝑟𝑦𝑥 = −
ℬ
𝑛𝑒
𝑅𝐻 = −
1
𝑛𝑒
Coeficiente Hall:
46
Efeito Hall
Modelo 2: dois portadores:
elétrons: massa efetiva 𝑚1 = 𝑚1∗ , densidade numérica 𝑛, tempo de relaxação
𝜏1 , frequência cíclotron 𝜔1 .
buracos: massa efetiva 𝑚2 = 𝑚2∗ , densidade numérica 𝑝, tempo de relaxação
𝜏2 , frequência cíclotron 𝜔2 .
47
Efeito Hall
Magnetocondutividade: soma das duas contribuições:
𝜎 ℬ =
𝐴1
𝐶1
−𝐶1
𝐴
+ 2
𝐴1
𝐶2
−𝐶2
𝐴 + 𝐴2
= 1
𝐴2
𝐶1 + 𝐶2
−𝐶1 − 𝐶2
𝐴1 + 𝐴2
onde:
𝐴𝑖 =
𝜎𝑖
1 + 𝜔𝑖2 𝜏𝑖2
𝑛𝑖 𝑒 2 𝜏𝑖
𝜎𝑖 =
𝑚𝑖
𝐶𝑖 =
𝜎𝑖 𝜔𝑖 𝜏𝑖
1 + 𝜔𝑖2 𝜏𝑖2
𝑒ℬ
𝜔𝑖 =
𝑚𝑖
48
Efeito Hall
Magnetoresistividade longitudinal:
𝑟𝑥𝑥
𝜎1 + 𝜎2 + 𝜎1 𝜔22 𝜏22 + 𝜎2 𝜔12 𝜏12
ℬ =
𝜎1 + 𝜎2 2 + 𝜎1 𝜔2 𝜏2 − 𝜎2 𝜔1 𝜏1
2
Se ℬ = 0, 𝜔1 = 𝜔2 = 0, e
𝑟𝑥𝑥 ℬ = 0 =
1
𝜎1 + 𝜎2
Note que 𝑟𝑥𝑥 ℬ > 𝑟𝑥𝑥 (0) para qualquer ℬ ≠ 0.
49
Efeito Hall
Se ocorrer
temos
𝜎1 𝜔2 𝜏2 = 𝜎2 𝜔1 𝜏1
𝑛=𝑝
Nesse caso, 𝑟𝑥𝑥 → ∞ se ℬ → ∞. Se 𝑛 ≠ 𝑝, 𝑟𝑥𝑥 satura quando ℬ → ∞.
50
Efeito Hall
Para a magnetoresistividade transversal, temos
𝑟𝑦𝑥
𝜎2 𝜔2 𝜏2 1 + 𝜔12 𝜏12 − 𝜎1 𝜔1 𝜏1 1 + 𝜔22 𝜏22
=
𝜎1 + 𝜎2 2 + 𝜎1 𝜔2 𝜏2 − 𝜎2 𝜔1 𝜏1 2
Quando ℬ → ∞, temos (verificar)
𝑟𝑦𝑥 =
e o coeficiente Hall fica
ℬ
𝑝−𝑛 𝑒
1
𝑅𝐻 =
𝑝−𝑛 𝑒
51
Efeito Hall Quântico
Em condutores bidimensionais, em baixas temperaturas e campos
magnéticos intensos, ocorre o efeito Hall quântico.
Curva da resistividade Hall (𝑟𝑦𝑥 ) em função de ℬ exibe platôs que são
múltiplos de
ℎ
= 25812,806 Ω
𝑒2
Correspondentemente, 𝑟𝑥𝑥 = 0 nesses platôs.
52
Efeito Hall Quântico
Os valores de 𝑟𝑦𝑥 são dados por
𝑟𝑦𝑥 =
ℎ 1
𝑒2 ℓ
ℓ ∈ ℤ: efeito Hall quântico usual.
𝑃
ℓ = , onde 𝑃, 𝑄 ∈ ℤ, 𝑄 ímpar:
𝑄
efeito Hall quântico fracionário.
53
Portadores em função de 𝑻
Queremos o número de portadores por volume em função de 𝑇.
Impurezas influenciam nos valores, mas é possível obter resultados
gerais, que não dependem disso.
Na BC, temos 𝑛𝑐 elétrons por volume e densidade de estados por
𝒟
volume 𝑔𝑐 𝜖 = 𝑐. Então,
𝑉
∞
𝑛𝑐 𝑇 =
𝑔𝑐 𝜖
𝜖𝑐
1
𝑒𝛽(𝜖−𝜇) + 1
𝑑𝜖
54
Portadores em função de 𝑻
Na BV, temos 𝑝𝑣 buracos por volume e densidade de estados por
𝒟
volume 𝑔𝑣 𝜖 = 𝑣. Então,
𝑉
𝜖𝑣
𝑝𝑣 𝑇 =
𝑔𝑣 𝜖
−∞
1
𝑒𝛽(𝜇−𝜖) + 1
𝑑𝜖
𝜇 é influenciado pelas impurezas. Para conhecer 𝜇, é preciso ter
informações sobre elas.
55
Portadores em função de 𝑻
Se ocorrer
𝜖𝑐 − 𝜇 ≫ 𝑘𝐵 𝑇
𝜇 − 𝜖𝑣 ≫ 𝑘𝐵 𝑇
é possível obter resultados importantes sem conhecer 𝜇 precisamente.
Se essa condição é válida, temos um semicondutor não degenerado.
Se não é valida, então o semicondutor é degenerado, e não é possível
usar os resultados abaixo.
56
Portadores em função de 𝑻
Considerando a condição de não degenerescência, temos (quadro):
∞
𝑛𝑐 𝑇 = 𝑒 −𝛽(𝜖𝑐 −𝜇)
𝑔𝑐 𝜖 𝑒 −𝛽(𝜖−𝜖𝑐 ) 𝑑𝜖
𝜖𝑐
Definimos
∞
𝑔𝑐 𝜖 𝑒 −𝛽(𝜖−𝜖𝑐 ) 𝑑𝜖
𝑁𝑐 𝑇 =
𝜖𝑐
57
Portadores em função de 𝑻
Então:
𝑛𝑐 𝑇 = 𝑒 −𝛽
𝜖𝑐 −𝜇
𝑁𝑐 𝑇
De forma similar, temos
𝜖𝑣
𝑃𝑣 𝑇 =
𝑔𝑣 𝜖 𝑒 −𝛽(𝜖𝑣 −𝜖) 𝑑𝜖
−∞
e
𝑝𝑣 𝑇 = 𝑒 −𝛽
𝜇−𝜖𝑣
𝑃𝑣 𝑇
58
Portadores em função de 𝑻
As energias envolvidas para os elétrons e buracos são da ordem de
𝑘𝐵 𝑇. Com isso, é possível escrever
1
𝑔𝑖 𝜖 = 2
2𝜋
2𝑚𝑖
ℏ2
3/2
𝜖 − 𝜖𝑖
e, considerando as bandas com forma parabólica em torno da base da
BC e do topo da BV, temos, para a BC,
ℏ2 𝑘 2
𝜖𝑘 = 𝜖𝑐 +
2𝑚𝑐
59
Portadores em função de 𝑻
Com isso, achamos (quadro)
1 2𝑚𝑐
𝑁𝑐 𝑇 =
4 𝜋𝛽ℏ2
3/2
1 2𝑚𝑣
𝑃𝑣 𝑇 =
4 𝜋𝛽ℏ2
3/2
e
60
Portadores em função de 𝑻
Então, obtemos
1 2𝑚𝑐
𝑛𝑐 𝑇 =
4 𝜋𝛽ℏ2
3/2
1 2𝑚𝑣
𝑝𝑣 𝑇 =
4 𝜋𝛽ℏ2
3/2
𝑒 −𝛽(𝜖𝑐 −𝜇)
e
𝑒 −𝛽(𝜇−𝜖𝑣 )
61
Portadores em função de 𝑻
A partir disso, obtemos
𝑛𝑐 𝑇 𝑝𝑣 𝑇 = 𝑁𝑐 𝑇 𝑃𝑣 𝑇 𝑒 −𝛽𝐸𝑔
que é a lei de ação de massas.
Para semicondutor intrínseco,
𝑛𝑐 𝑇 = 𝑝𝑣 𝑇 = 𝑛𝑖 𝑇
62
Portadores em função de 𝑻
Então,
1
2
𝑛𝑖 𝑇 =
4 𝜋𝛽ℏ2
3/2
𝑚𝑐 𝑚𝑣
3/4 −𝛽𝐸𝑔 /2
𝑒
Além disso, achamos também (quadro)
𝜇 𝑇 = 𝜖𝑣 +
𝐸𝑔 3
𝑚𝑣
+ 𝑘𝐵 𝑇 ln
2 4
𝑚𝑐
63
Portadores em função de 𝑻
Ex.:
64
Portadores em função de 𝑻
Semicondutor extrínseco:
𝑛𝑐 − 𝑝𝑣 = Δ𝑛 (≠ 0)
Lei de ação de massas é válida, e escrevemos
𝑛𝑐 𝑇 𝑝𝑣 𝑇 = 𝑛𝑖2
Desenvolvendo, chegamos a (quadro)
𝑛𝑐
=
𝑝𝑣
Δ𝑛
2
2
+ 4𝑛𝑖2
±
Δ𝑛
2
65
Portadores em função de 𝑻
Obtemos, também,
Δ𝑛
= 2 sinh 𝛽 𝜇 − 𝜇𝑖
𝑛𝑖
que indica qual a importância das impurezas para o número de
portadores.
Note que
𝜖𝑐 − 𝜇𝑖 ≫ 𝑘𝐵 𝑇
𝜇𝑖 − 𝜖𝑣 ≫ 𝑘𝐵 𝑇
Δ𝑛/𝑛𝑖 só é apreciável quando 𝜇 não é comparável a 𝜇𝑖 .
66
Portadores em função de 𝑻
Semicondutor não degenerado: 𝜇 ∼ 𝑂(𝜇𝑖 ) e
impurezas não são importantes.
Δ𝑛
𝑛𝑖
≪ 1 ⇒ níveis de
Nesse caso,
𝑛𝑐
Δ𝑛
𝑛𝑖2
Δ𝑛
=
+
±
𝑝𝑣
2
Δ𝑛 2
2
A concentração do portador majoritário é
outro portador.
Δ𝑛 2
𝑛𝑖
vezes maior que a do
67
Portadores em função de 𝑻
Se Δ𝑛 > 0, 𝑛𝑐 ≫ 𝑝𝑣 , e temos um semicondutor tipo 𝑛 (excesso de
elétrons).
Se Δ𝑛 < 0, 𝑝𝑣 ≫ 𝑛𝑐 , e o semicondutor é tipo 𝑝 (excesso de buracos).
68
Portadores em função de 𝑻
Vamos agora estimar a influência de 𝑇 nos níveis das impurezas.
Os níveis das impurezas doadoras ficam em 𝜖𝑑 , logo abaixo de 𝜖𝑐 . Os
níveis aceitadores ficam em 𝜖𝑎 , logo acima de 𝜖𝑣 .
Há 𝑁𝑑 impurezas doadoras por volume, e 𝑁𝑎 impurezas aceitadoras
por volume.
Portadores em níveis de impurezas não interagem (hipótese).
69
Portadores em função de 𝑻
Cada nível doador pode estar vazio, ter um elétron ou dois elétrons.
Essa última configuração tem energia muito alta, e é pouco provável.
Número médio de ocupação de um nível qualquer (Termodinâmica:
grande-canônico)
𝑛 =
𝑁𝑗 𝑒 −𝛽(𝐸𝑗 −𝜇𝑁𝑗)
𝑒 −𝛽(𝐸𝑗 −𝜇𝑁𝑗)
70
Portadores em função de 𝑻
Para um dado nível doador, temos 𝑁𝑗 = 0 ou 𝑁𝑗 = 1 (↑ ou ↓).
𝑛 =
1
1
1 + 2 𝑒𝛽(𝜖𝑑 −𝜇)
Assim, o número médio de elétrons nos níveis doadores é
𝑛𝑑 =
𝑁𝑑
1
1 + 2 𝑒𝛽(𝜖𝑑 −𝜇)
71
Portadores em função de 𝑻
Para os níveis aceitadores, a ideia é similar, trocando-se elétrons por
buracos. Assim,
𝑝𝑎 =
𝑁𝑎
1
1 + 2 𝑒𝛽(𝜇−𝜖𝑎)
Queremos generalizar a condição 𝑛𝑐 = 𝑝𝑣 válida para equilíbrio
térmico em semicondutores intrínsecos.
72
Portadores em função de 𝑻
Conservação de carga:
𝑛𝑐 + 𝑛𝑑 − 𝑝𝑣 + 𝑝𝑎 = 𝑁𝑑 − 𝑁𝑎
Condição para semicondutor não degenerado:
𝜖𝑑 − 𝜇 ≫ 𝑘𝐵 𝑇
𝜇 − 𝜖𝑎 ≫ 𝑘𝐵 𝑇
73
Portadores em função de 𝑻
Se esta condição é verificada, ocorre
𝑛𝑑 ≪ 𝑁𝑑 ,
𝑝𝑎 ≪ 𝑁𝑎
Assim, praticamente todos os níveis de impurezas estão ionizados
(vazios – doadores, com elétrons – aceitadores).
Conservação de carga fica
𝑛𝑐 + 𝑛𝑑 = 𝑁𝑑 − 𝑁𝑎 = Δ𝑛
74
Portadores em função de 𝑻
Então,
𝑛𝑐
1
=
𝑝𝑣
2
𝑁𝑑 − 𝑁𝑎
2
1/2
+ 4𝑛𝑖2
1
± (𝑁𝑑 − 𝑁𝑎 )
2
e
𝑁𝑑 − 𝑁𝑎
= 2 sinh 𝛽 𝜇 − 𝜇𝑖
𝑛𝑖
75
Portadores em função de 𝑻
Regime intrínseco: 𝑛𝑖 ≫ |𝑁𝑑 − 𝑁𝑎 |:
𝑛𝑐
1
= 𝑛𝑖 ± (𝑁𝑑 − 𝑁𝑎 )
𝑝𝑣
2
Regime extrínseco: 𝑛𝑖 ≪ |𝑁𝑑 − 𝑁𝑎 |:
𝑛𝑐
1
𝑛𝑖2
= 𝑁𝑑 − 𝑁𝑎 +
𝑝𝑣
2
𝑁𝑑 − 𝑁𝑎
2
1
𝑁𝑑 − 𝑁𝑎 ± 𝑁𝑑 − 𝑁𝑎
2
76
Portadores em função de 𝑻
Se 𝑁𝑑 > 𝑁𝑎 :
𝑛𝑐 = 𝑁𝑑 − 𝑁𝑎 ,
𝑛𝑖2
𝑝𝑣 =
𝑁𝑑 − 𝑁𝑎
𝑛𝑖2
𝑛𝑐 =
,
𝑁𝑎 − 𝑁𝑑
𝑝𝑣 = 𝑁𝑎 − 𝑁𝑑
Se 𝑁𝑑 < 𝑁𝑎 :
77
Portadores em função de 𝑻
Em baixas temperaturas, ou para altas concentrações de impurezas,
𝑛
𝑝
uma das frações 𝑑 ou 𝑎 (não ambas) pode deixar de ser desprezível
𝑁𝑑
𝑁𝑎
⇒ nível não está totalmente ionizado.
A densidade de portadores dominante diminui com 𝑇.
78
Portadores em função de 𝑻
Outro efeito em 𝑇 baixa é a possibilidade de ocorrer tunelamento
entre os níveis de impurezas, por causa da superposição das funções
de onda ⇒ hopping.
79
Portadores em função de 𝑻
Ge dopado com Sb
80
Junção 𝒑𝒏
Vamos agora investigar um dispositivo formado por semicondutores:
junção pn.
81
Junção 𝒑𝒏
Hipóteses:
1. Semicondutor tipo n: apenas níveis doadores, tipo p: apenas níveis
aceitadores.
2. 1D (direção x).
3. Junção ocorre em 𝑥 = 0. Região de depleção: −𝑑𝑝 < 𝑥 < 𝑑𝑛 .
4. Impurezas tipo n: densidade 𝑁𝑎 (𝑥). Tipo p: densidade 𝑁𝑑 (𝑥).
5. Densidades dadas por
𝑁𝑑 𝑥 =
𝑁𝑑 ,
0,
𝑥>0
𝑥<0
𝑁𝑎 𝑥 =
0,
𝑁𝑎 ,
𝑥>0
𝑥<0
6. Impurezas ionizadas ⇒ saturação longe da junção.
82
Junção 𝒑𝒏
Considere os semicondutores separados:
Tipo 𝑛: 𝜇 entre 𝐸𝑐 e 𝐸𝑑 .
Tipo 𝑝: 𝜇 entre 𝐸𝑣 e 𝐸𝑎 .
Diferença: 𝑒Δ𝜙.
83
Junção 𝒑𝒏
Colocando os semicondutores em contato:
84
Junção 𝒑𝒏
A diferença no potencial químico gera fluxo de elétrons do lado 𝑛
para o 𝑝.
O lado 𝑝 fica negativo
na região da junção. O
lado 𝑛 fica positivo.
Surge campo elétrico na
junção.
BV e BC na região 𝑝 são
mais altos que na região
𝑛. Diferença: 𝑒Δ𝜙.
85
Junção 𝒑𝒏
O campo elétrico orienta-se de 𝑛 → 𝑝. O potencial elétrico
correspondente aumenta de 𝑝 → 𝑛.
Eles aparecem numa região chamada de região de depleção. Fora dela
o potencial é constante e o campo é nulo.
Em geral, há circulação de cargas nos dois sentidos.
86
Junção 𝒑𝒏
Num dado instante, algum elétron da BV na região 𝑝 é excitado
termicamente à BC da região 𝑝.
Posteriormente, ele pode seguir para a BC da região 𝑛. Isso dá origem
à corrente térmica.
Noutro instante, algum elétron num nível da BC do lado 𝑛 abaixo da
BC do lado 𝑝, pode sofrer flutuação em energia e atingir energia
compatível com a BC-𝑝, passando para ela. Essa é a corrente de
recombinação.
87
Junção 𝒑𝒏
No equilíbrio térmico, sem
potencial externo, a corrente
total é nula.
A aplicação de uma tensão
externa modifica o
comportamento da corrente de
recombinação, sem alterar a
corrente térmica.
88
Junção 𝒑𝒏
O potencial elétrico altera o hamiltoniano do sistema da seguinte
forma:
ℋ𝑛 = ℰ𝑛 𝑘 − 𝑒𝜙 𝑥
Com isso, temos
𝑛𝑐 𝑥 = 𝑁𝑐 𝑇 𝑒 −𝛽(𝜖𝑐 −𝑒𝜙
𝑥 −𝜇)
e
𝑝𝑣 𝑥 = 𝑃𝑣 𝑇 𝑒 −𝛽 𝜇−𝜖𝑣 +𝑒𝜙
𝑥
89
Junção 𝒑𝒏
Saturação (longe da junção):
𝑁𝑑 = 𝑛𝑐 ∞ = 𝑁𝑐 𝑇 𝑒 −𝛽(𝜖𝑐 −𝑒𝜙
∞ −𝜇)
𝑁𝑎 = 𝑝𝑣 −∞ = 𝑃𝑣 𝑇 𝑒 −𝛽 𝜇−𝜖𝑣 +𝑒𝜙
−∞
Graficamente
90
Junção 𝒑𝒏
Definindo:
Δ𝜙 = 𝜙 ∞ − 𝜙(−∞)
temos a condição (quadro)
𝑁𝑎 𝑁𝑑
𝑒Δ𝜙 = 𝐸𝑔 + 𝑘𝐵 𝑇 ln
𝑁𝑐 𝑃𝑣
que é uma condição de contorno para o problema.
91
Junção 𝒑𝒏
Para achar 𝜙 𝑥 , é preciso trabalhar com a equação de Poisson (em
1D):
𝑑2𝜙
𝜚 𝑥
𝛻 𝜙=
=−
𝑑𝑥 2
𝜖
2
Na saturação:
𝜚 𝑥 = −𝑒[𝑛𝑐 𝑥 − 𝑝𝑣 𝑥 + 𝑁𝑎 𝑥 − 𝑁𝑑 (𝑥)
Em princípio, combinar estas equações resulta numa equação
diferencial solúvel numericamente.
92
Junção 𝒑𝒏
Estimativa mais útil (quadro): potencial só varia na região de
depleção: −𝑑𝑝 ≤ 𝑥 ≤ 𝑑𝑛 . A densidade fica
𝜚 𝑥 =
0,
−𝑒𝑁𝑎 ,
𝑒𝑁𝑑 ,
0,
𝑥<−𝑑𝑝
−𝑑𝑝 <𝑥<0
0<𝑥<𝑑𝑛
𝑥>𝑑𝑛
Para 𝑥 < −𝑑𝑝 e 𝑥 > 𝑑𝑛 , o campo é nulo, e o potencial é constante.
93
Junção 𝒑𝒏
Após resolver a equação de Poisson, o potencial fica
𝜙 𝑥 = 𝜙 −∞ ,
𝜙 𝑥 = 𝜙 −∞ +
𝑒𝑁𝑎
𝑥 + 𝑑𝑝
2𝜖
𝑒𝑁𝑑
𝜙 𝑥 =𝜙 ∞ −
𝑥 − 𝑑𝑛
2𝜖
𝜙 𝑥 =𝜙 ∞ ,
𝑥 < −𝑑𝑝
2
2
,
,
−𝑑𝑝 < 𝑥 < 0
0 < 𝑥 < 𝑑𝑛
𝑥 > 𝑑𝑛
94
Junção 𝒑𝒏
Graficamente:
95
Junção 𝒑𝒏
A continuidade do campo e do potencial em 𝑥 = 0 fornece
𝑁𝑎 𝑑𝑝 = 𝑁𝑑 𝑑𝑛
e
Δ𝜙 =
𝑒
(𝑁𝑎 𝑑𝑝2 + 𝑁𝑑 𝑑𝑛2 )
2𝜖
Com isso, é possível determinar a largura da região de depleção.
96
Junção 𝒑𝒏
Para 𝑑𝑝 , temos
𝑁𝑑
1
2𝜖Δ𝜙
𝑑𝑝 =
𝑁𝑎 𝑁𝑑 + 𝑁𝑎 𝑒
1/2
e, para 𝑑𝑛 , ficamos com
𝑁𝑎
1
2𝜖Δ𝜙
𝑑𝑛 =
𝑁𝑑 𝑁𝑑 + 𝑁𝑎 𝑒
1/2
97
Junção 𝒑𝒏
Largura total:
𝑁𝑎 + 𝑁𝑑 2𝜖Δ𝜙
𝑤 = 𝑑𝑛 + 𝑑𝑝 =
𝑁𝑎 𝑁𝑑
𝑒
1/2
Ex.: para Δ𝜙 ∼ 1 V, 𝜖 = 10−10 F/m e 𝑁𝑎 , 𝑁𝑑 na faixa 1014 a 1018
portadores/cm3, temos 𝑤 ∼ 102 − 104 Å e campos da ordem de
105 − 107 V/m.
98
Junção 𝒑𝒏
Na junção pn usual, 𝑁𝑎 ∼ 𝑁𝑑 e ambos não são muito grandes.
É interessante considerar o caso onde 𝑁𝑎 , 𝑁𝑑 ou ambos são grandes.
Temos as junções
p+n:𝑁𝑎 ≫ 𝑁𝑑 .
pn+: 𝑁𝑑 ≫ 𝑁𝑎 .
p+n+: ambos são grandes.
99
Junção homopolar
Podemos combinar portadores de mesmo tipo, formando junções
homopolares, onde apenas um tipo de portador é relevante.
p+p: acúmulo de buracos no lado p.
n+n: acúmulo de elétrons no lado n.
Elas facilitam a condução, ao contrário da junção pn.
100
Junção sob Tensão Externa
Vamos agora considerar o efeito da aplicação de uma tensão externa à
junção.
Ocorre deslocamento do equilíbrio sob tensão externa.
Recordando, na junção elétrons passam naturalmente do lado 𝑛 para o
𝑝.
Considere uma fonte de tensão contínua, com terminais (+) e (-).
101
Junção sob Tensão Externa
Ao conectar o terminal (+) no lado 𝑛 e o (-) no 𝑝, o campo elétrico na
região da junção fica mais intenso.
A altura da barreira de potencial aumenta.
O efeito é dificultar a passagem de elétrons no sentido 𝑛 → 𝑝.
Com isso, a corrente de recombinação diminui.
102
Junção sob Tensão Externa
A corrente térmica não é alterada, pois depende apenas de 𝑇.
Assim, elétrons vão de 𝑝 → 𝑛, e corrente flui de 𝑛 → 𝑝.
Essa é a corrente de polarização reversa, e é pequena.
103
Junção sob Tensão Externa
Conectando o terminal (+) ao lado p e o (-) ao n, a situação se inverte.
A altura de barreira diminui, o campo elétrico fica menos intenso, e a
corrente de recombinação cresce muito.
Há corrente elétrica no sentido 𝑝 → 𝑛. Esta é a corrente de
polarização direta, que é 4-5 ordens de grandeza maior que a reversa
(tipicamente).
104
Junção sob Tensão Externa
Vamos considerar que 𝑉 > 0 corresponde à polarização direta, e 𝑉 <
0 à reversa.
105
Junção sob Tensão Externa
Diferença de potencial na junção sob tensão externa:
Δ𝜙 = Δ𝜙0 − 𝑉
Δ𝜙0 : ddp para 𝑉 = 0 (situação de equilíbrio).
A aplicação da tensão externa altera os limites da região de depleção:
𝑁𝑑
1
2𝜖 Δ𝜙0 − 𝑉
𝑑𝑝 =
𝑁𝑎 𝑁𝑑 + 𝑁𝑎
𝑒
1/2
𝑁𝑎
1
2𝜖 Δ𝜙0 − 𝑉
𝑑𝑛 =
𝑁𝑑 𝑁𝑑 + 𝑁𝑎
𝑒
1/2
106
Junção sob Tensão Externa
Largura total:
𝑁𝑎 + 𝑁𝑑 2𝜖 Δ𝜙0 − 𝑉
𝑤 = 𝑑𝑛 + 𝑑𝑝 =
𝑁𝑎 𝑁𝑑
𝑒
1/2
Interessa-nos investigar as correntes na região da junção pn.
Convenção:
𝑗: densidade de corrente elétrica.
𝒥: densidade de corrente numérica.
107
Junção sob Tensão Externa
Relação entre as densidades:
𝑗𝑒 = −𝑒𝒥𝑒 ,
𝑗ℎ = 𝑒𝒥ℎ
Quando 𝑉 = 0, 𝒥𝑒 = 𝒥ℎ = 0 ⇒ compensação entre corrente térmica
e de recombinação.
Para elétrons:
𝒥𝑒 = 𝒥𝑒term 𝑒 𝛽𝑒𝑉 − 1
𝒥𝑒term : densidade numérica de corrente térmica em 𝑉 = 0.
108
Junção sob Tensão Externa
Para buracos:
𝒥ℎ = 𝒥ℎterm 𝑒 𝛽𝑒𝑉 − 1
𝒥𝑒term : densidade numérica de corrente térmica em 𝑉 = 0.
Densidade resultante (vetorial):
𝑗 = 𝑒 𝒥ℎterm + 𝒥𝑒term 𝑒 𝛽𝑒𝑉 − 1
Como determinar os coeficientes? Outra abordagem.
109
Junção sob Tensão Externa
Correntes podem ser geradas por campos elétricos ou por gradientes
de concentração de portadores (correntes de difusão). Em 1D:
𝒥ℎ = 𝜇ℎ 𝑝𝑣 𝐸 − 𝐷𝑝
𝑑𝑝𝑣
𝑑𝑥
𝒥𝑒 = −𝜇𝑒 𝑛𝑐 𝐸 − 𝐷𝑛
𝑑𝑛𝑐
𝑑𝑥
Estas equações combinam as relações
𝑗 = 𝜎𝐸
𝑗 = −𝐷𝛻ϱ
110
Junção sob Tensão Externa
𝜇𝑒 e 𝜇ℎ : mobilidade de elétrons e buracos (𝜇𝑖 > 0).
A mobilidade é dada por
De
𝑗 = 𝜚𝑣
sai
𝜎𝑒 = 𝑒𝑛𝜇𝑒
𝜎ℎ = 𝑒𝑝𝜇ℎ
𝜇=
𝑣
𝐸
𝜎 = 𝜎ℎ + 𝜎𝑒 = 𝑒(𝜇𝑒 𝑛 + 𝜇ℎ 𝑝)
111
Junção sob Tensão Externa
𝐷𝑝 e 𝐷𝑛 : coeficientes de difusão para buracos e elétrons.
São grandezas positivas, e relacionadas com 𝜇𝑖 pelas relações de
Einstein:
𝑒𝐷𝑛
𝜇𝑒 =
𝑘𝐵 𝑇
𝑒𝐷𝑝
𝜇ℎ =
𝑘𝐵 𝑇
112
Junção sob Tensão Externa
A condutividade pode ser modelada por
𝑛𝑒 2 𝜏
𝜎=
𝑚
Com isso, a mobilidade pode ser escrita como
𝑒𝜏𝑒col
𝜇𝑒 =
𝑚𝑒
𝑒𝜏ℎcol
𝜇ℎ =
𝑚ℎ
𝜏𝑖col : tempo médio de colisões para o portador i.
𝑚𝑖 : massa efetiva do portador i.
113
Junção sob Tensão Externa
Equação de continuidade:
𝛻⋅𝑗+
𝜕𝜚
=0
𝜕𝑡
Escrevendo em termos das densidades numéricas, temos
𝜕𝑛𝑒
𝜕𝒥𝑒
=−
𝜕𝑡
𝜕𝑥
𝜕𝑝𝑣
𝜕𝒥ℎ
=−
𝜕𝑡
𝜕𝑥
Entretanto, estas equações não consideram a transferência de cargas
entre as bandas.
114
Junção sob Tensão Externa
Levando em conta as transferências de cargas, obtemos
𝜕𝑛𝑒
𝑑𝑛𝑐
=
𝜕𝑡
𝑑𝑡
𝜕𝒥𝑒
−
𝜕𝑥
𝑔−𝑟
𝜕𝑝𝑣
𝑑𝑝𝑣
=
𝜕𝑡
𝑑𝑡
𝜕𝒥ℎ
−
𝜕𝑥
𝑔−𝑟
Índice g-r: geração – recombinação. Modelo para essas taxas:
𝑑𝑛𝑐
𝑑𝑡
𝑔−𝑟
𝑛𝑐 − 𝑛𝑐0
=−
𝜏𝑛
𝑑𝑝𝑣
𝑑𝑡
𝑔−𝑟
𝑝𝑣 − 𝑝𝑣0
=−
𝜏𝑝
𝑛𝑖0 : valores de equilíbrio.
𝜏𝑖 : tempo médio de recombinação.
115
Junção sob Tensão Externa
Note que, em geral, 𝜏𝑖 ≫ 𝜏𝑖col , pois as colisões são intrabandas e as
recombinações são interbandas.
Tipicamente, 𝜏𝑖col ∼ 10−12 - 10−13 s, e 𝜏𝑖 ∼ 10−3 - 10−8 s.
Com isso, temos
𝜕𝑛𝑒
𝑛𝑐 − 𝑛𝑐0 𝜕𝒥𝑒
=−
−
𝜕𝑡
𝜏𝑛
𝜕𝑥
𝜕𝑝𝑣
𝑝𝑣 − 𝑝𝑣0 𝜕𝒥ℎ
=−
−
𝜕𝑡
𝜏𝑝
𝜕𝑥
116
Junção sob Tensão Externa
Situação estacionária para 𝑉 ≠ 0:
𝜕𝒥𝑒 𝑛𝑐 − 𝑛𝑐0
+
=0
𝜕𝑥
𝜏𝑛
𝜕𝒥ℎ 𝑝𝑣 − 𝑝𝑣0
+
=0
𝜕𝑥
𝜏𝑝
Caso particular: ℰ pequeno e concentração de portadores majoritários
constante:
𝑑 2 𝑛𝑐 𝑛𝑐 − 𝑛𝑐0
𝐷𝑛
−
=0
𝑑𝑥 2
𝜏𝑛
𝑑 2 𝑝𝑣 𝑝𝑣 − 𝑝𝑣0
𝐷𝑝
−
=0
𝑑𝑥 2
𝜏𝑝
117
Junção sob Tensão Externa
Comprimentos de difusão: distâncias características em que as
concentrações voltam aos valores de equilíbrio.
𝐿𝑛 =
𝐷𝑛 𝜏𝑛
𝐿𝑝 =
𝐷𝑝 𝜏𝑝
Solução considerando que estamos do lado 𝑛 da junção:
𝑝𝑣 = 𝑝𝑣 ∞ + 𝑝𝑣 𝑥0 − 𝑝𝑣 ∞ 𝑒 −(𝑥−𝑥0)/𝐿𝑝
118
Junção sob Tensão Externa
Estimativa para as densidades numéricas de corrente:
𝒥ℎ𝑡𝑒𝑟𝑚
𝑛𝑖2 𝐿𝑝
=
𝑁𝑑 𝜏𝑝
𝒥𝑒𝑡𝑒𝑟𝑚
𝑛𝑖2 𝐿𝑛
=
𝑁𝑎 𝜏𝑛
A densidade de corrente fica
𝑗 = 𝑒𝑛𝑖2
Lembrar que
𝐷𝑝
𝐷𝑛
+
𝑁𝑎 𝐿𝑛 𝑁𝑑 𝐿𝑝
1 2𝑚𝑐
2
𝑛𝑖 =
4 𝜋𝛽ℏ2
3/2
𝑒 𝛽𝑒𝑉 − 1
1 2𝑚𝑣
4 𝜋𝛽ℏ2
3/2
𝑒 −𝛽𝐸𝑔
119
Junção sob Tensão Externa
Corrente de saturação: 𝑉 → −∞:
𝑗=
−𝑒𝑛𝑖2
𝐷𝑝
𝐷𝑛
+
𝑁𝑎 𝐿𝑛 𝑁𝑑 𝐿𝑝
120
Junção sob Tensão Externa
Se 𝑉 > 0 → polarização direta: corrente apreciável.
Se 𝑉 < 0 → polarização reversa: corrente baixa.
retificador
121
Transistor
𝑝+ : altamente dopada: emissor.
𝑛: fracamente dopada e fina: base.
𝑝: moderadamente dopada: coletor
𝑉𝐸 > 0:
polarização
direta emissorbase.
𝑉𝐶 ≪ 0:
polarização
reversa basecoletor.
122
Transistor
Praticamente toda a corrente que entra no emissor segue para o
coletor: 𝐼𝐶 ∼ 𝐼𝐸 .
Como 𝑉𝐶 ≫ 𝑉𝐸 , temos um amplificador de potência.
123