Apresentação do PowerPoint

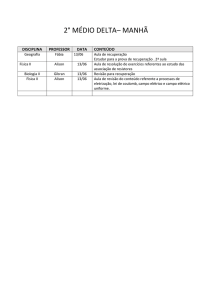
Campos de cargas aceleradas
•
Imageamento: Método de Monte Carlo
•
Campo eletromagnético de cargas aceleradas
- radiação e força de reação radiativa
- campo de carga em movimento hiperbólico
- evolução do campo elétrico no espaço-tempo
•
Campo gravitacional uniforme
- movimento hiperbólico e o Princípio da Equivalência
- transformações de Rindler
- mapeamento e o horizonte de eventos
- campo eletrostático de uma carga em repouso
- massas inercial e gravitacional de partículas carregadas
- campo de carga em queda livre
- equações de Maxwell
Imageamento via simulação de Monte Carlo
Seleção dos pontos: técnica de rejeição de Neuman
Imageamento via simulação de Monte Carlo
Efeito Aharanov-Bohm
Imageamento via simulação de Monte Carlo
Tunelamento quântico
Imageamento via simulação de Monte Carlo
Orbitais do átomo de hidrogênio
Campo elétrico de uma carga em movimento uniforme
Campo elétrico coulombiano
Campo elétrico de uma carga em movimento uniforme , 𝛽 = 0,9
Campo elétrico de uma carga em movimento uniforme, 𝛽 = 0,99
Campo elétrico de uma carga em movimento uniforme, 𝛽 = 0,999
Campo elétrico de uma carga em movimento hiperbólico
Movimento hiperbólico: trajetória, velocidade, aceleração
Campo elétrico de carga em movimento hiperbólico, 𝑎 𝑐 2 = 0,5 𝐿−1
Energia eletrostática
e
raio clássico do elétron
Problemas
•
A massa de elétron pode ser de origem unicamente eletromagnética?
Cargas aceleradas: radiação e força de reação radiativa
Força
de
reação radiativa
(não relativístico)
Força de reação radiativa = auto interação
Auto interação e renormalização de massa
Auto interação com campos retardado e avançado
Transformações de Rindler
Mapeamento do referencial não inercial R para o inercial R’
Transformações de Rindler
Mapeamento do referencial inercial R’ para
o não inercial R
Horizonte de eventos: regiões acessíveis e não
acessíveis para observadores não inerciais
Campo elétrico de uma carga em repouso num campo gravitacional uniforme,
para 𝑔 𝑐 2 = 0,1 𝐿−1
Campo elétrico de uma carga em repouso num campo gravitacional uniforme.
para 𝑔 𝑐 2 = 0,5 𝐿−1
Problemas
•
•
O observador no referencial inercial R’ vê radiação eletromagnética.
Em princípio pode medir a força de reação radiativa.
•
O observador no referencial não inercial R não vê nenhuma radiação (conservação de
energia).
E a força de reação radiativa?
•
Movimento de queda livre
Campo elétrico de uma carga em queda livre campo gravitacional uniforme
𝑔 𝑐 2 = 0,5 𝐿−1
Campo elétrico de uma carga em queda livre campo gravitacional uniforme
𝑔 𝑐 2 = 1 𝐿−1
Trabalhos relacionados
•
•
•
•
•
M. Goto, H. Iwamoto, V. M. de Aquino e V. C. Aguilera-Navarro, Monte Carlo
image representation, American Journal of Physics 69, n.3, p. 1-5 (2001).
M. Goto et al, On the Equivalence Principle and gravitational and inertial mass
relation of classical charged particles, Class. Quantum Grav. 27 (2010) 025005.
M. Goto , Campo eletrostático de uma carga em repouso num campo gravitacional
uniforme, Rev. Bras. de Ensino de Física, v.31, n.4, 4307 (2009).
M. Goto , Campo eletromagnético de uma carga em queda livre num campo
gravitacional uniforme, Rev. Bras. de Ensino de Física, v.32, n.1, 1310 (2010).
M. Goto , Uniform Gravitational Field Environment for Classical Charged Particle,
CQG (2010)
FIM