Gravitação

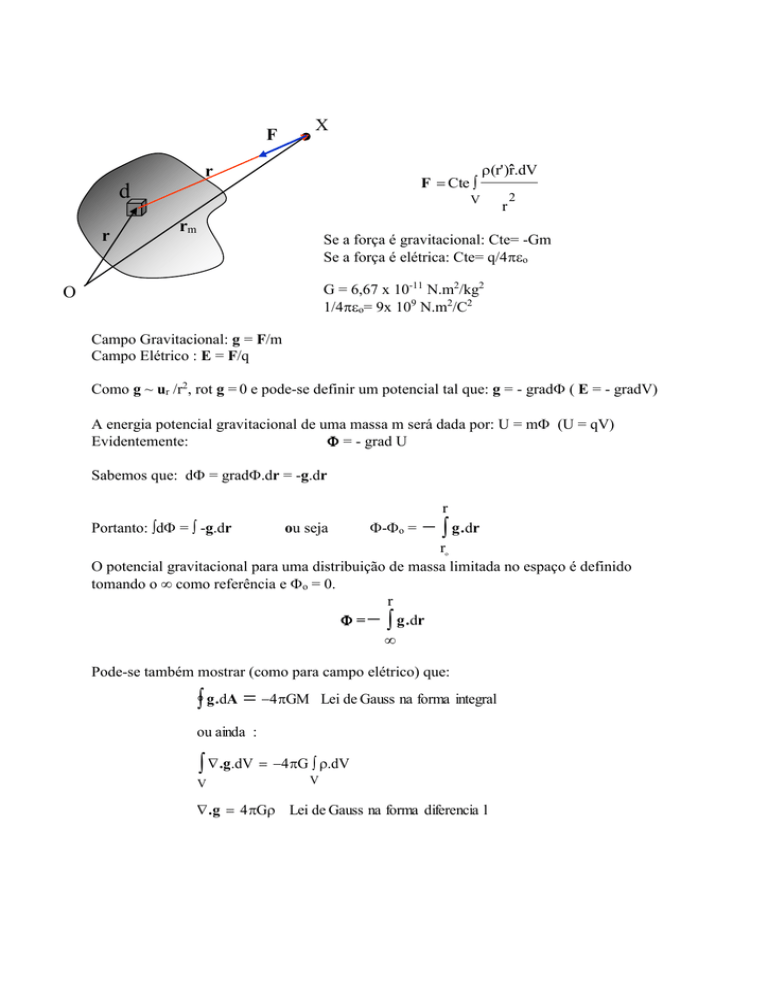
X
F
r
d
V
r
’
F  Cte 
(r' )ˆr.dV
V
rm
r
2
Se a força é gravitacional: Cte= -Gm
Se a força é elétrica: Cte= q/4o
G = 6,67 x 10-11 N.m2/kg2
1/4o= 9x 109 N.m2/C2
O
Campo Gravitacional: g = F/m
Campo Elétrico : E = F/q
Como g ~ ur /r2, rot g = 0 e pode-se definir um potencial tal que: g = - grad E = - gradV)

A energia potencial gravitacional de uma massa m será dada por: U = mU = qV)
Evidentemente:
 = - grad U
Sabemos que: d = grad.dr = -g.dr
r
Portanto: ∫d = ∫ -g.dr
ou seja
-o =
  g .dr
ro
O potencial gravitacional para uma distribuição de massa limitada no espaço é definido
tomando o ∞ como referência e o = 0.
r
 =   g .dr

Pode-se também mostrar (como para campo elétrico) que:
 g .dA  4 GM
Lei de Gauss na forma integral
ou ainda :
  .g.dV  4 G  .dV
V
V
 .g  4 G Lei de Gauss na forma diferencia l