Ângulos ao centro e inscritos

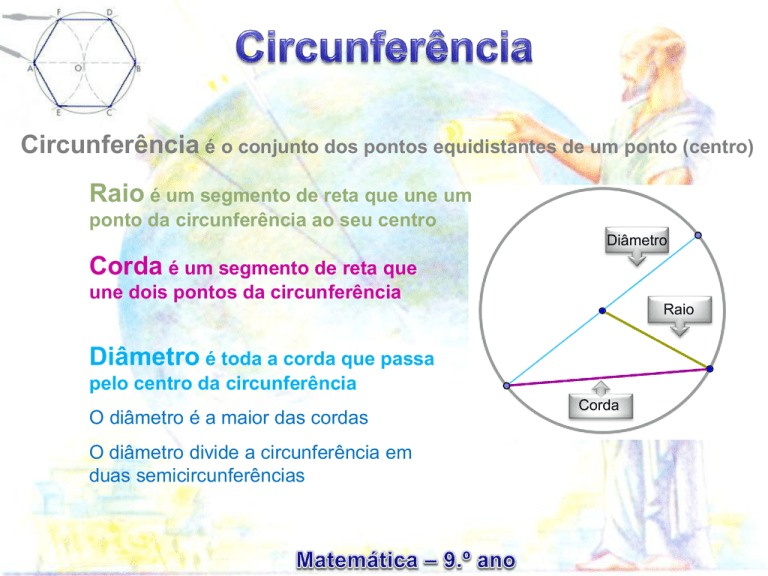
Circunferência é o conjunto dos pontos equidistantes de um ponto (centro)
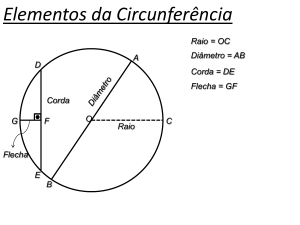
Raio é um segmento de reta que une um
ponto da circunferência ao seu centro
Diâmetro
Corda é um segmento de reta que
une dois pontos da circunferência
Raio
Diâmetro é toda a corda que passa
pelo centro da circunferência
O diâmetro é a maior das cordas
O diâmetro divide a circunferência em
duas semicircunferências
Corda
Pág.9 – exercício 3
Observa a figura e diz se é verdadeira ou falsa cada uma das
seguintes afirmações:
a) A circunferência desenhada tem centro
em O e raio [BD];
F
b) [AO] é um diâmetro;
F
c) [OB] é um raio;
V
d) [BC] é um diâmetro;
F
e) [BC] é uma corda;
V
f)
V
[BD] é um diâmetro;
g) [BD] é uma corda;
V
BD  2  AO.
V
h)
Ângulo ao Centro e Arco de Circunferência
A
c
Um ângulo formado por dois raios designa-se
ângulo ao centro (o vértice do ângulo coincide
com o centro da circunferência)
B
Qualquer porção da circunferência determinada
por dois dos seus pontos, que são os extremos
do arco designa-se Arco de circunferência.
Nota – Quando falamos em arco, sem nada
acrescentar referimo-nos ao arco menor
AB
 Ao ângulo ao centro ACB corresponde a
corda [AB] e o arco [AB] e vice-versa.
 Numa circunferência, qualquer ângulo que
não seja ao centro diz-se excêntrico.
Pág.12 – exercício 1
Observa a circunferência de centro O da figura:
a)
Identifica quatro ângulos ao centro. AOB ; BOC ; COD e EOD
b)
Indica dois pares de ângulos ao BOC  FOE
centro geometricamente iguais.
c)
Classifica quanto aos lados o triângulo
[EOD].
Triângulo isósceles
AOB  EOD
A
D
Numa circunferência:
C
- a cada ângulo ao centro
corresponde um arco e vice-versa
- A arcos iguais correspondem
cordas e ângulos ao centro iguais
- A ângulos ao centro iguais
B
E
F
G
correspondem arcos e cordas iguais
- A cordas iguais correspondem
arcos e ângulos ao centro iguais
- A amplitude de um arco é igual à amplitude
do ângulo ao centro correspondente
H
C
I
Pág.13 – exercício 3
Observa a figura onde
Prova que MA  AT  TE  EM
Resposta:
MA  AT  TE  EM
Esta afirmação é verdadeira porque se
[MT]  [EA], então:
M OA  90º , AOT  90º , T OE  90º e EOM  90º
Como
a
ângulos
ao
centro
iguais
correspondem arcos e cordas iguais,
podemos concluir que:
MA  AT  TE  EM
Pág.13 – exercício 4
Na figura abaixo, [AD] é um diâmetro da circunferência de

centro O, AOB  60º e OC é a bissectriz do ângulo BOD.
a) Calcula BOC e COD. BOC  60º; COD  60º
b) Que podemos concluir em relação a
AB , BC , CD. Porquê? A amplitude dos
arcos é 60º porque a amplitude dos ângulos ao
centro correspondentes também é 60º.
c) E em relação a AB , BC e CD. Porquê?
P  d 
Os comprimentos das cordas são iguais
porque a arcos e ângulos ao centro iguais
correspondem cordas iguais
AO  2 cm , calcula o comprimento do arco AB.
2
P
4
2
Se AO  2cm, r  2cm e d  4cm log o AB 


cm.
6
6 2 3
d) Supondo que
Pág.23 – exercício 1 a) e c)
Observa as figuras e determina, em cada caso, os valores de x e y.
a)
Ângulos verticalmente opostos
x
y  30º e x  30º
y
c)
x+30º 2x - 10º
x  30º  2 x  10º 
 x  2 x  10º 30º 
 1x  40º 
 x  40º
Ângulo inscrito
F
Um ângulo formado por duas cordas designase
c
E
ângulo inscrito
(o vértice do ângulo
coincide com um ponto da circunferência)
D
80º
A amplitude de um ângulo inscrito é igual
a
metade
da
amplitude
do
arco
compreendido entre os seus lados
O ângulo ao centro tem de amplitude 80º, logo a
amplitude do arco correspondente também é 80º, o
que significa que a amplitude do ângulo inscrito é
igual a metade da do arco correspondente (80º/2=40º).
Pág.15 – exercício 6
Observa a figura e indica:
a) Um ângulo ao centro;
AOC
b) Um ângulo inscrito;
ABC
c) Um arco de circunferência;
AB
d) Um raio de circunferência;
OC 
e) Uma corda da circunferência.
 AB