Momento de uma força

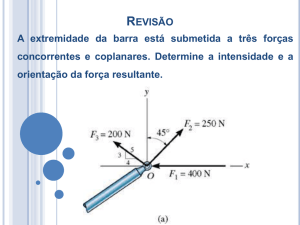
EQUILÍBRIO DE UM PONTO MATERIAL
 Diz-se
que um ponto material está em equilíbrio
quando a resultante de todas as forças que atuam
nele é nula. O ponto material permanecerá em
repouso, se estava inicialmente em repouso, ou em
movimento retilíneo com velocidade constante, se
assim estava inicialmente.
 Pode-se representar o equilíbrio de um ponto
material a partir das componentes da resultante,
onde:
Σ Fx= 0
Σ Fy= 0 Σ Fz= 0
Determine a força necessária no cabos AB e AC
para suportar o farol de tráfego de 12 kg.
Determinar as forças nos cabos, sabendo que a luminária
possui uma massa de 50 kg. (g = 10 m/s2).
TORQUE (MOMENTO)
Deriva da palavra latina “torcer”
Ponto de aplicação
( ponto em que a força é aplicada )
Linha de ação da força
( reta que contém o vetor força )
PONTO DE APLICAÇÃO DA FORÇA F
Ponto de aplicação:
A – gira sentido horário;
B – gira sentido anti-horário.
C – não gira.
s = linha de ação – efeito é o
mesmo.
MOMENTO DE UMA FORÇA – FORMAÇÃO ESCALAR

Quando uma força é aplicada a um corpo,
ela produzirá uma tendência de rotação do
corpo em torno de um ponto que não está
na linha de ação da força. Essa tendência de
rotação algumas vezes é chamada de
torque, mas normalmente é denominada
momento de uma força, ou simplesmente
momento.
OBSERVE A FIGURA
PORTÃO
EM QUE PONTO É MAIS FÁCIL ABRIR O PORTÃO?
(OBSERVE O PONTO DE APLICAÇÃO E A DISTÂNCIA D)
Portão visto de cima
PARA 90º O EFEITO DA FORÇA É MÁXIMO?
(OBSERVE A LINHA DE AÇÃO DA FORÇA E A DISTÂNCIA D)
MOMENTO
A
figura abaixo mostra uma partícula
localizada pelo vetor posição r , sob a ação
de uma força F
O
momento exercido por uma força sobre
a partícula, é uma grandeza vetorial, e é
definido como:
 
  r F

M  r  F  sen
MOMENTO TENDE A PRODUZIR ROTAÇÃO
SENTIDOS POSSÍVEIS – CONVENÇÃO DE SINAIS.
anti-horário
horário
MOMENTOS DAS FORÇAS EM RELAÇÃO AO PONTO O.
MOMENTO RESULTANTE
O momento resultante nessa figura é:
EXERCÍCIO
SOLUÇÃO
SOLUÇÃO ITEM ( A )
SOLUÇÃO ITEM ( B )
OBSERVAÇÃO
EQUILÍBRIO
 Condições
 Diz-se
para o equilíbrio de um corpo
que um corpo está em equilíbrio
quando a soma das forças que atuam
sobre o mesmo e a soma dos momentos
que agem sobre ele forem nulos.
BIBLIOGRAFIA






BEER, F. P.; JOHNSTON JR, E. R.; EISENBERG, E. R.
Mecânica vetorial para engenheiros: estática. 7.ed. SP: McGraw
Hill - Artmed, 2006.
CRAIG JR, R. R. Mecânica dos materiais. 2. ed. RJ: LTC, 2002.
HIBBELER, R. C. Estática: mecânica para engenharia. v.1. 12.
ed. SP: Pearson, 2011.
RESNICK, R.; HALLIDAY, D.; MERRILL, J. Fundamentos de
física. Vol.1. 8 ed. Rio de Janeiro: LTC, 2009.
SEARS, ZEMANSKY & YOUNG, Eletromagnetismo. Vol I. 10 ed.
São Paulo: Pearson Addison Wesley, 2006.
TIPLER, Paul A.; MOSCA, Gene.. Física: Eletricidade,
Magnetismo e Ótica. Vol. I. 6 ed. Rio de Janeiro: LTC, 2009.